Другий алгоритм дослідження функції на екстремум

1. Знайти стаціонарні точки заданої функції.

2. Знайти похідну другого порядку.

3. Обчислити значення похідної другого порядку в стаціонарних точках і для визначення екстремальних точок, користуючись другою достатньою умовою існування екстремуму.

4. Обчислити значення функції в точках екстремуму (див. приклад 9.6).

Зауваження. Другий алгоритм є більш зручним, ніж перший. Проте, якщо друга похідна в стаціонарній точці перетворюється в нуль, то краще користуватися першим алгоритмом дослідження функції на екстремум.

9.4.5. Відшукання найбільшого і найменшого значень функції на відрізку

Нехай на відрізку задано неперервну функцію f. Тоді на цьому відрізку функція f досягає найбільшого і найменшого значень, тобто існують точки з відрізка , в яких функція f набуває найбільшого і найменшого на значень. Припустимо спочатку, що функція f не має на відрізку критичних точок. Тоді вона на цьому відрізку зростає або спадає. Це означає, що свого найбільшого і найменшого значень функція набуває на кінцях відрізка.

Нехай тепер функція f має на відрізку скінченну кількість критичних точок. Ці точки поділяють відрізок на скінченну кількість відрізків, всередині яких критичні точки відсутні. Тому найбільшого і найменшого значень функція f набуває на кінцях таких відрізків, тобто в критичних точках або в точках a і b.

Алгоритм знаходження найбільшого та найменшого значення функції f на відрізку .

1. Знайти критичні точки функції f в інтервалі .

2. Обчислити значення функції в усіх критичних точках.

3. Обчислити значення функції на кінцях відрізка, тобто обчислити і .

4. Порівняти отримані значення функції в критичних точках і на кінцях відрізка ; найбільше і найменше з усіх таких чисел і будуть відповідно найбільшим і найменшим значеннями функції f на відрізку (див. приклад 9.7).



Приклади

Приклад. 9.1. Дано функцію . Знайти приріст , якщо і .

 . Для , . 

Приклад 9.2. Визначити інтервали зростання і спадання функції .

 Функція f визначена і диференційована в інтервалі . Її похідна . Знайдемо точки, в яких ця похідна дорівнює нулю . Оскільки похідна – неперервна функція в інтервалі , то вона зберігає знак в інтервалах і . Значення похідної в точці від’ємне, а в точці додатне. Тому для всіх і для всіх (див. рис.). Функція спадає і зростає в інтервалі .

Приклад 9.3. Довести, що точка є точкою максимуму функції :

1) ; 2)) .

 1) Візьмемо інтервал , який містить точку . Оскільки функція в точці дорівнює одиниці, а для всіх х з інтервалу , , то є точкою максимуму функції . Число 1 є максимумом функції .

2 ) Візьмемо інтервал , який містить точку (тут ). Тоді , а для всіх х, , з інтервалу . Отже, точка є точкою максимуму функції 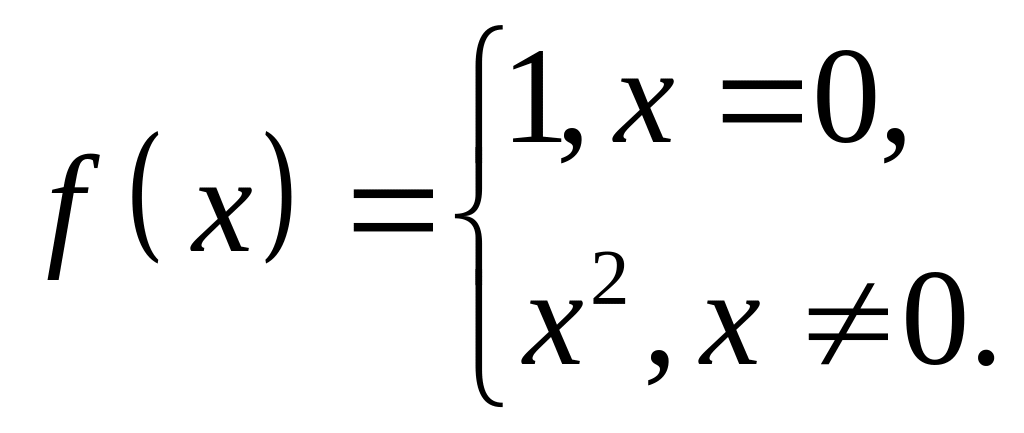, а число 1 є максимумом заданої функції. Зазначимо, що задана функція не є неперервною в точці (див рис.). 

Приклад 9.4. Довести, що точка є точкою мінімуму .

Візьмемо інтервал , який містить точку . Оскільки у точці дорівнює –1, а для всіх х з інтервалу , то є точкою мінімуму функції . Число –1 є мінімумом функції .

Приклад 9.5. Дослідити на екстремум функції:

1) ; 2) .

 1) Маємо . Прирівнявши похідну до нуля і розв'язавши рівняння, знаходимо стаціонарні точки . Точок, в яких похідна не існує, немає. Згідно з пунктами 3) і 4) алгоритму послідовно заповнюємо рядки таблиці:

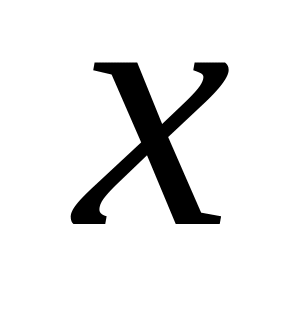
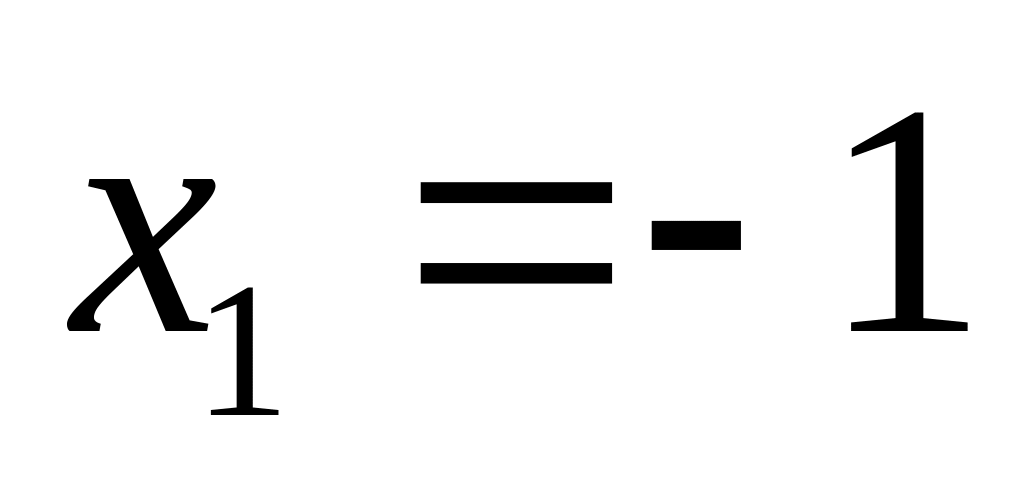
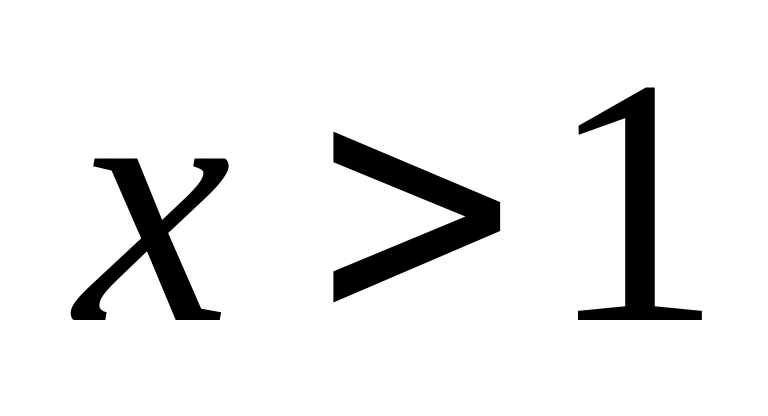
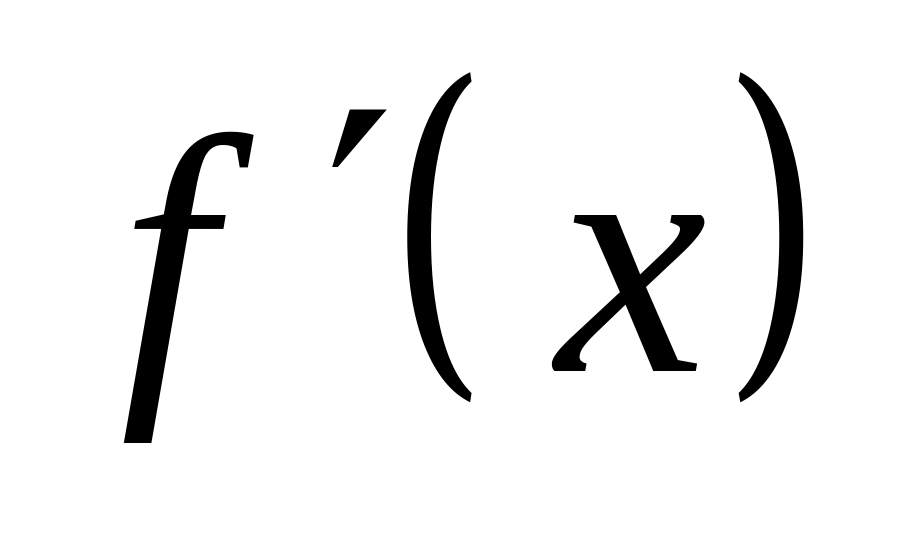
	+	0	–	0	+
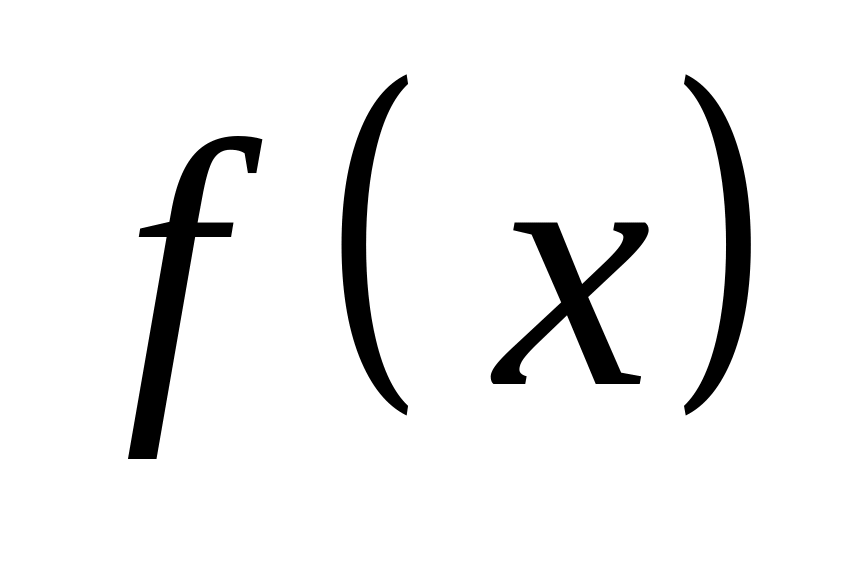
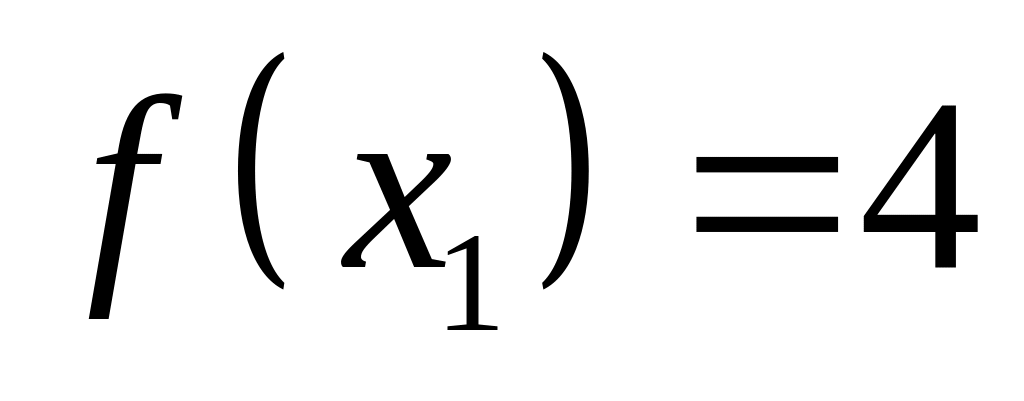
		Максимум		Мінімум	

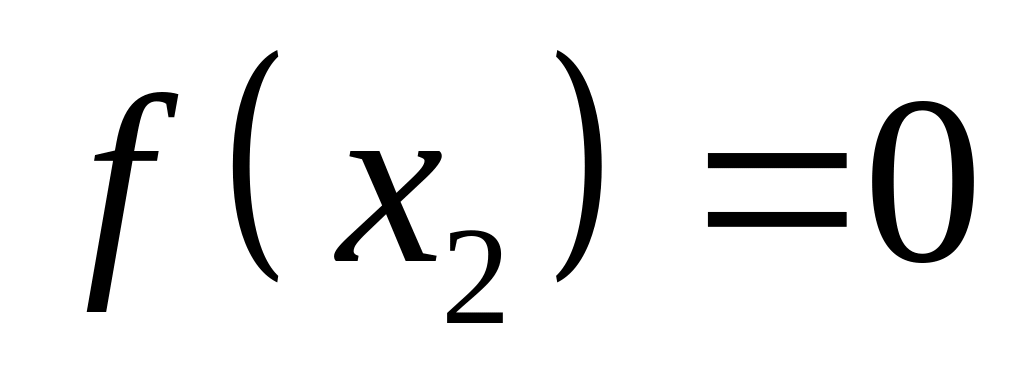
2) Стаціонарних точок задана функція не має, оскільки , а точці похідна не існує. Тому критичною точкою є тільки одна точка . Оскільки зліва від похідна , а справа і функція неперервна в цій точці, то є точкою мінімуму, мінімум функції . 

Приклад 9.6. Дослідити на екстремум функцію .

 Маємо:

1) ;

2) ;

3) . Отже, в точці функція має максимум, а в точці – мінімум;

4) . 

Приклад 9.7. Знайти найбільше і найменше значення функції на відрізку .

 Спочатку знайдемо критичні точки. Оскільки похідна визначена для будь-якого дійсного числа, то залишається розв’язати рівняння . Тепер треба вибрати найбільше і найменше з чисел . Таким чином, – найбільше значення, – найменше значення. 

	Питання для самоперевірки

1. Дайте означення приросту аргумента та функції.

2. Сформулюйте ознаки зростання та спадання функції.

3. Що називається границею функції в точці та на нескінченості?

4. В чому полягають основін теореми про границі?

5. Дайте означення і запишіть формули асимптот графіка функції.

6. В якому випадку функція є диференційованою?

7. Сформулюйте алгоритм знаходження похідної функції за означенням.

8. Запишіть формули похідних основних функцій.

9. В чому полягають правила диференціювання.

10. Дайте означення і запишіть формули дотичної та нормалі, проведених до графіка функції.

11. Яка функція називається зростаючою та спадною?

12. Що називається точкою максимуму, мінімуму, екстремуму функції?

13. Сформулюйте необхідну та достатню умови екстремуму.

14. Запишіть алгоритм дослідження функції на екстремум.

15. Як знаходити найбільше і найменше значення функції на відрізку?



Вправи

1. Обчислити:

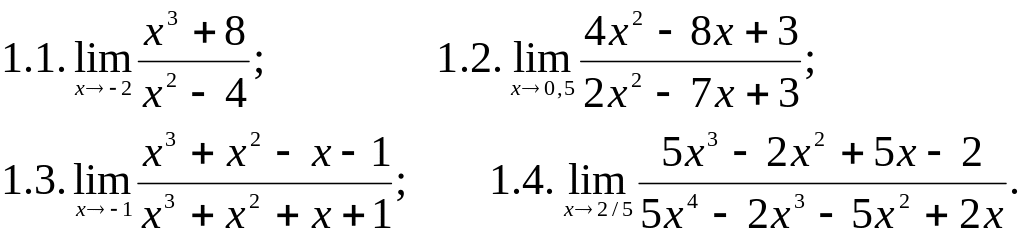
2. Обчислити значення похідних заданих функцій при вказаних значеннях незалежної змінної

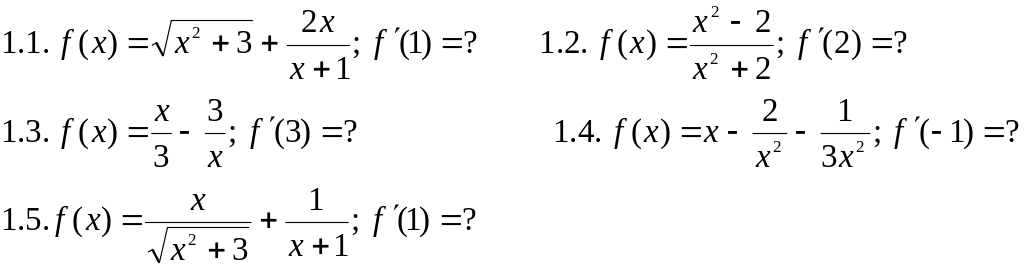3. В яких точках дотичні до кривої паралельні прямій

4. У яких точках дотична до графіка функції утворить з віссю Ох кут 45⁰?

5. Під яким кутом до осі Ох нахилена дотична, проведена до кривої в точці її перетину з віссю Оу?

6. Під яким кутом до осі Ох нахилена дотична, проведена до кривої в точці

7. Відомо, що пряма є дотичною до лінії, що задана рівнянням Знайти координати точки дотику.

8. Скласти рівняння дотичної до графіка функції в точці

9. Функція задана формулою Показати, що ця функція зростає в будь-якій точці, що належить її області визначення.

10. Функція задана формулою Знайти всі значення постійної а, при яких дана функція визначена і зростає при всіх

11. Знайти похідні функцій

1. 2.

3. 4.

89