9.4.2. Екстремуми функції

Я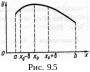 кщо існує інтервал , де , який міститься в проміжку і такий, що для всіх х з інтервалу , то точку називають точкою максимуму функції , а саме число – максимумом функції (рис. 9.5). Іншими словами, функція f має в точці максимум, якщо для досить малого приросту (довільного знаку) виконується нерівність (див. приклад 9.3).

Я кщо існує інтервал , який міститься у проміжку і такий, що для всіх х з інтервалу , , то точку називають точкою мінімуму функції , а саме число – мінімумом функції (рис. 9.6). Іншими словами, функція f має в точці мінімум, якщо для досить малого приросту (довільного знаку) виконується нерівність .

Точки максимуму і мінімуму функції називають екстремальними точками, а максимум і мінімум називають екстремумом функції (від латин. extremum – крайній). Тобто екстремальні точки – це такі точки, в яких функція набуває відповідно найбільшого та найменшого значень порівняно із значеннями функції, які вона набуває в точках, досить близьких до екстремальної точки. Такий екстремум називають локальним (слово «локальний» походить від латинського слова lokalis, що означає «місцевий»). Тому не слід плутати максимум (мінімум) з найбільшим (найменшим) значенням функції, якого вона досягає на проміжку .

9.4.3. Необхідна та достатня умови екстремуму

Д ля функції, яка визначена на проміжку , глобальним (абсолютним) максимумом називається найбільше значення функції на всьому проміжку. Глобальним мінімумом називається значення функції, найменше серед значень на всьому проміжку. На рис. 9.7 точки є точками локального максимуму, а точки – точками локального мінімуму. Глобальний мінімум досягається на одному з кінців проміжку, тобто в точці а, а глобальний максимум збігається з локальним максимумом у точці . Локальних максимумів і мінімумів на проміжку може бути кілька, тоді як найбільше (найменше) значення, якщо воно існує, єдине. Окремий локальний мінімум може бути більшим за окремий локальний максимум. Так, мінімум у точці більший за максимум у точці .

Необхідні умови існування екстремуму функції): якщо функція у внутрішній точці проміжку має екстремум і в цій точці існує похідна, то , причому якщо при переході точки через точку похідна змінює знак з плюса на мінус, то точка є точкою максимуму функції, якщо ж при переході точки через точку похідна змінює знак з мінуса на плюс, то точка є точкою мінімуму функції.

9.4.4. Алгоритми дослідження функції на екстремум Перший алгоритм дослідження функції на екстремум

1. Знайти стаціонарні точки заданої функції. Для цього слід розв’язати рівняння та із розв’язків вибрати тільки дійсні і ті, які є внутрішніми точками області існування функції.

2. Знайти точки, в яких похідна не існує (але функція ) існує. Якщо критичних точок функція не має, то вона не має і екстремальних точок. Така функція не має екстремуму.

3. Якщо критичні точки є, то розбити числову вісь на проміжки, в кожному з яких дослідити знак похідної функції першого порядку, встановити поведінку функції (зростає чи спадає) і перевірити зміну знаку похідної при переході через критичні точки, якщо знак змінюється, то визначити вид екстремуму.

4. Обчислити значення функції в точках екстремуму (див. приклад 9.5).

Друга достатня умова існування екстремуму: нехай функція диференційована в околі стаціонарної точки , а в самій точці має похідну другого порядку, причому . Якщо , то функція точці має мінімум. Якщо , то функція в точці має максимум.