Ч ЕРКАСЬКИЙ ДЕРЖАВНИЙ БІЗНЕС-КОЛЕДЖ

Підготовчий курс з математики

Тема 9. Похідна

	довідковий матеріал

9.1. Основні поняття

9.1.1. Приріст аргументу і приріст функції

Нехай – функція, х і – два значення незалежної змінної з ; тоді різниця називається приростом незалежної змінної (або приростом аргументу) в точці і позначається (читається "дельта ікс"). Отже,

(9.1)

З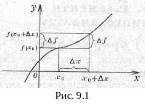 рівності (9.1) випливає, що , тобто початкове значення змінної дістало приріст . Відповідно і значення функції зміниться:

(9.2)

Різниця між новим значенням функції і її початковим значенням називається приростом функції в точці і позначається символом (читається "дельта f в точці "), тобто

(9.3)

Приріст функції f у даній точці ще позначають через або (мал. 9.1).

При знаходженні приросту функції замість незалежної змінної підставляють її приріст (див. приклад 9.1).

9.1.2. Ознаки зростання або спадання функції

Функція зростає на прозміжку тоді і тільки тоді, коли для будь-яких значень і з проміжку виконується нерівність

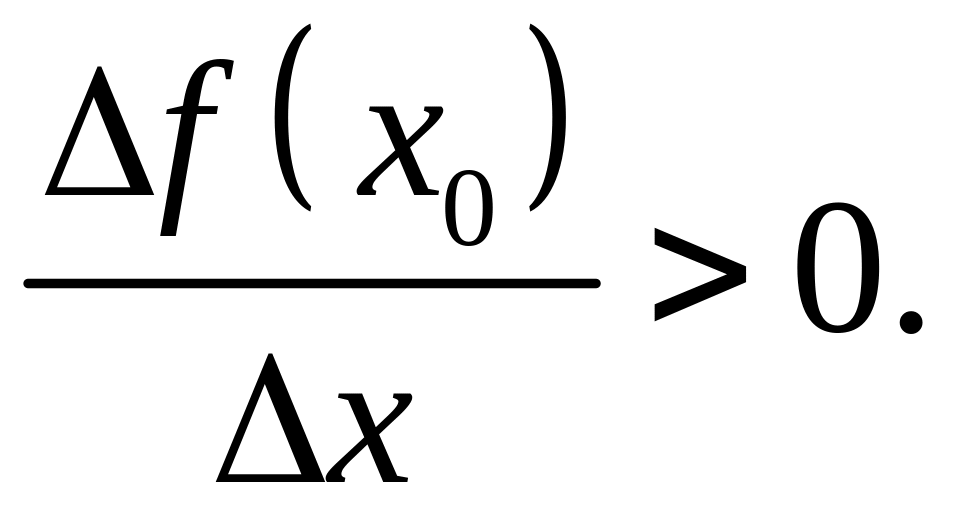
Функція спадає на проміжку тоді і тільки тоді, коли для будь-яких значень і з проміжку виконується нерівність

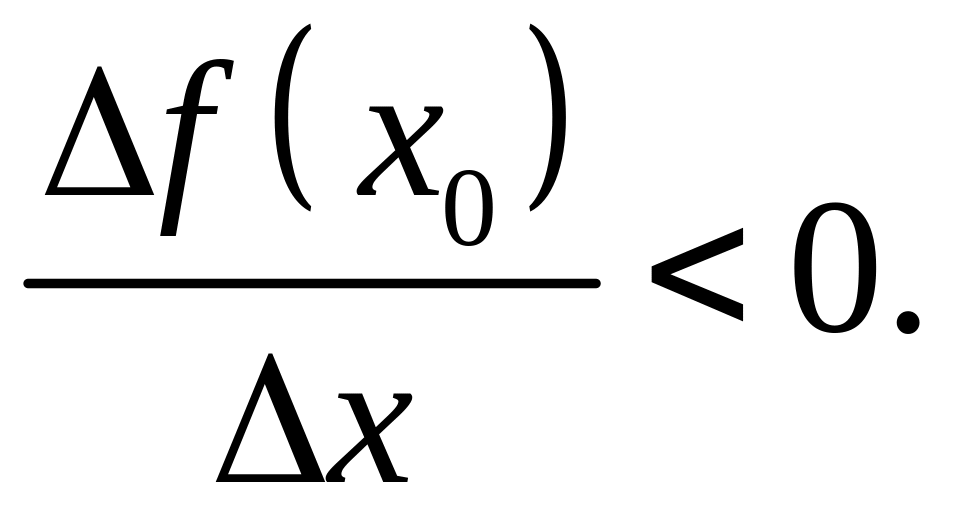
9.2. Границя функції

9.2.1. Основні поняття

Нагадаємо, що будь-який інтервал, що містить точку а, називається околом точки а. Симетричний інтервал називається -околом точки а. Запис , означає, що число х належить -околу точки а.

Число b називається границею функції при , якщо для будь-якого додатного числа знайдеться таке додатне число , що для всіх , що задовольняють нерівності , справедлива нерівність . Це записують так:

О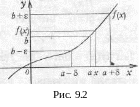 скільки нерівність рівносильна подвійній нерівності , а нерівність – подвійній нерівності , то означення границі функції в точці можна дати так: число b є границею функції при , якщо, який би не був -окіл точки b, знайдеться такий -окіл точки а, що для будь-якого значення , яке належить -околу точки а, значення належить -околу точки b (мал. 9. 2).

Із означення границі функції випливає, що функція має бути визначена на проміжку , крім, можливо, самої точки а.

Теорема 9.1. Якщо функція має границю при , то ця границя єдина.

Число А називається границею функції при , якщо для будь-якого існує число таке, що коли . Основні властивості границі функції при такі самі, як границі числової послідовності.

9.2.2. Теореми про границі

На практиці границю функції в точці визначають не на основі наведеного вище означення, а застосовуючи теореми про границі функцій, аналогічні теоремам про границі числових послідовностей. Наведемо ці теореми.

Якщо при існують границі функцій і , тоді

1) ;

2) ;

3) 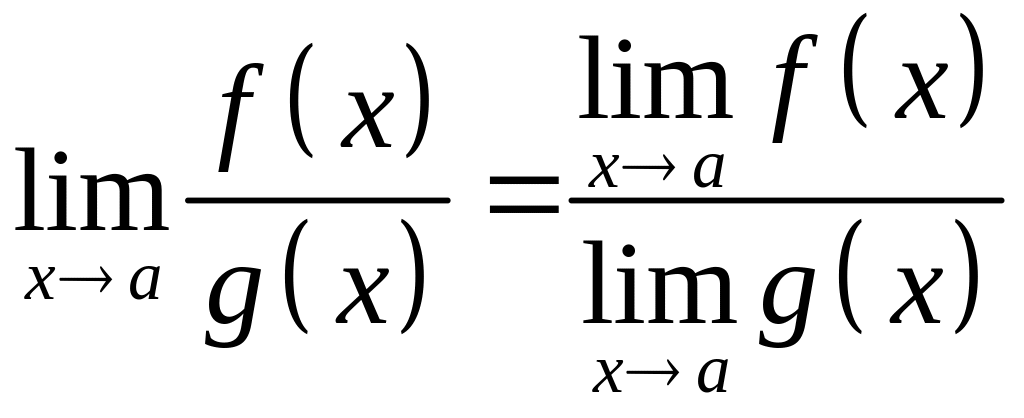, де .

Наслідок. , де k – сталий множник.

З цих теорем випливає, зокрема, що границя многочлена при дорівнює , тобто

9.2.3. Асимптоти графіка функції

Асимптотою кривої називається пряма, до якої крива може необмежено наближатися. Іншими словами, пряма називається асимптотою графіка функції при , якщо різниця – нескінченно мала при .

Аналогічно означають асимптоти і при .

Теорема 9.2. Якщо пряма – асимптота графіка функції при , то

(9.4)

Зокрема, якщо існує , то 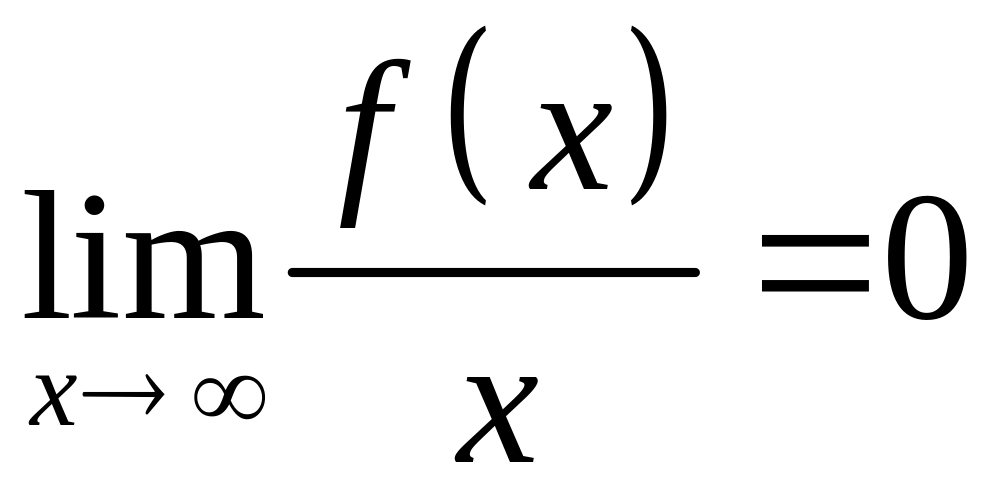, оскільки обмежена, а – нескінченно мала при . В цьому разі , і асимптота має рівняння ; в цьому разі асимптота називається горизонтальною. Якщо , асимптота називається похилою.

Наведемо тепер означення вертикальної асимптоти.

Нехай функція визначена на деякому проміжку . Якщо при , то пряма називається вертикальною асимптотою графіка функції при зправа. А якщо при , то пряма називається вертикальною асимптотою графіка функції при зліва.

Отже, графік функції може мати такі асимптоти:

вертикальну асимптоту – пряму , якщо ;

горизонтальну асимптоту – пряму , якщо ;

похилу асимптоту – пряму , де ;

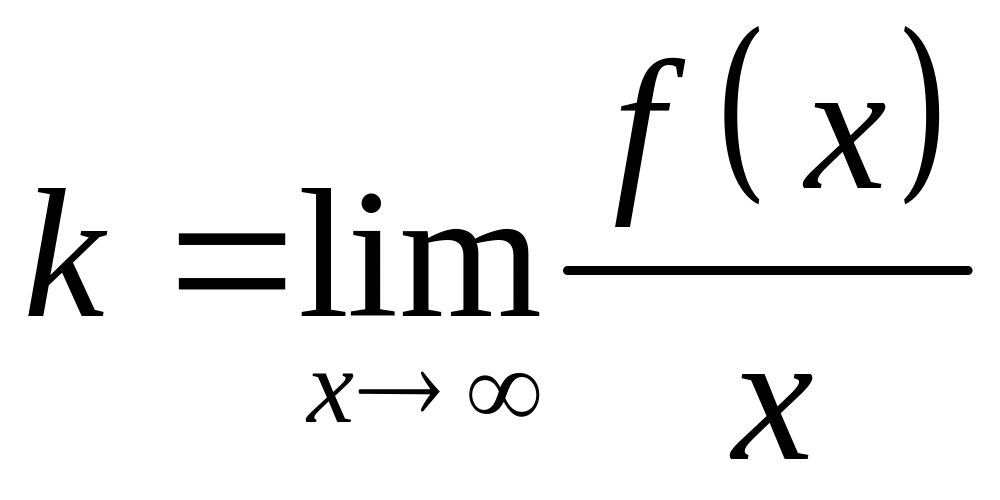( означає або ).