2. Сколько существует четырёхзначных пин-кодов?

На самом деле для решения задачи достаточно знаний правил комбинаторики:  способами можно выбрать первую цифру пин-кода и  способами – вторую цифру пин-кода и столькими же способами – третью и столькими же – четвёртую. Таким образом, по правилу умножения комбинаций, четырёхзначный пин-код можно составить:  способами.

А теперь с помощью формулы. По условию нам предложен набор из  цифр, из которого выбираются  цифры и располагаются в определенном порядке, при этом цифры в выборке могут повторяться (т.е. любой цифрой исходного набора можно пользоваться произвольное количество раз). По формуле  количества размещений с повторениями:

3. В студенческой столовой продают сосиски в тесте, ватрушки и пончики. Сколькими способами можно приобрести пять пирожков?

Сразу обратите внимание на типичный критерий сочетаний с повторениями – по условию на выбор предложено не множество объектов как таковое, а различные виды объектов; при этом предполагается, что в продаже есть не менее пяти хот-догов, 5 ватрушек и 5 пончиков. Пирожки в каждой группе, разумеется, отличаются – ибо абсолютно идентичные пончики можно смоделировать разве что на компьютере =) Однако физические характеристики пирожков по смыслу задачи не существенны, и хот-доги / ватрушки / пончики в своих группах считаются одинаковыми.

Что может быть в выборке? Прежде всего, следует отметить, что в выборке обязательно будут одинаковые пирожки (т.к. выбираем 5 штук, а на выбор предложено 3 вида). Варианты тут на любой вкус: 5 хот-догов, 5 ватрушек, 5 пончиков, 3 хот-дога + 2 ватрушки, 1 хот-дог + 2 + ватрушки + 2 пончика и т.д.

Как и при «обычных» сочетаниях, порядок выбора и размещение пирожков в выборке не имеет значения – просто выбрали 5 штук и всё.

Используем формулу  количества сочетаний с повторениями:  способом можно приобрести 5 пирожков.

4. В биномиальном разложении найти член разложения, не содержащий х

Так как в разложении мы ищем член не содержащий х, то

Тогда

5. Доказать, что при любом натуральном n число делится на 9

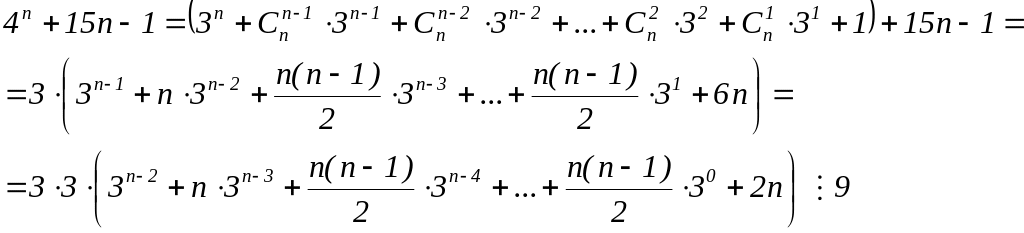
6. Сколько имеется костей в обычной игре «домино»?

Кости домино можно рассматривать как сочетания с повторениями по две из семи цифр множества (0, 1, 2, 3, 4, 5, 6). Воспользуемся формулой .

Число всех таких сочетаний равно .

Задания для самостоятельного решения

І. Перестановки, размещения, сочетания без повторения

Задача 1. Сколько двузначных чисел можно составить, используя цифры 7, 4, 5?

Задача 2. Сколько трехзначных чисел можно составить, используя цифры 7, 4, 5?

Задача 3. Сколько натуральных чисел, меньших 1000, можно записать, используя цифры 7, 4 и 5?

Задача 4. Сколько всего четырехзначных чисел можно составить из цифр 0 и1?

Задача 5. Сколько трехзначных чисел можно записать, используя цифры 0, 1, 3, 6, 7 и 9, если каждая из них может быть использованы в записи только один раз?

Задача 6. 9 карточек пронумерованы числами  1, 2, 3, 4, 5, 6, 7, 8, 9. Из этих карточек четыре наугад взятых карточки выкладываем в ряд. Сколько при этом можно получить различных четырехзначных чисел?

Задача 7. Сколько существует способов выбрать троих ребят из четверых желающих дежурить по столовой?

Задача 8. В библиотеке читателю предложили на выбор из новых поступлений 10 книг и 4 журнала. Сколькими способами он может выбрать из них 3 книги и 2 журнала?

Задача 9. Порядок выступления 7 участников конкурса определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?

Задача 10. В шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия?

Задача 11. Учащимся дали список из 10 книг, которые рекомендуется прочитать во время каникул. Сколькими способами ученик может выбрать из них 6 книг?

Задача 12. На полке стоит 12 книг: англо-русский словарь и 11 художественных произведений на английском языке. Сколькими способами читатель может выбрать 3 книги, если:

1. Словарь нужен ему обязательно;

2. Словарь ему не нужен?

Задача 13. Сколькими различными способами можно расставить на полке собрание сочинений, состоящее из 10-ти томов, при условии, что первый и пятый тома не должны стоять рядом.

Задача 14. Автокомбинат имеет 7 автомобилей малой грузоподъёмности и 10 большегрузных автомобилей. Нужно выбрать 3 автомобиля малой грузоподъёмности для обслуживания трёх торговых организаций и 5 большегрузных автомобилей для работы на стройке. Сколькими способами автокомбинат может осуществить свой выбор?

Задача 15. Имеется пять кусков материи разных цветов. Сколько из этих кусков можно сшить различных флагов, если флаги состоят из трёх горизонтальных полос, причём две соседние полосы должны быть разного цвета?

Задача 16. У Деда Мороза в мешке 7 одинаковых подарков, которые можно произвольным образом распределить среди 5-ти детей. Сколькими способами можно это сделать?

Задача 17. Сколько различных раскладов можно получить, раздавая колоду из 52-х карт четырём игрокам?

Задача 18. Сколько различных раскладов можно получить, раздавая колоду из 52-х карт четырём игрокам, при условии, что каждый игрок получает одного туза?

Задача 19. У Деда Мороза в мешке 7 различных подарков, которые можно произвольным образом распределить среди 5-ти детей. Сколькими способами можно это сделать?