5.2. Схематизация реальных объектов и свойств материалов

Для решения вопроса о прочности реальной конструкции необходимо правильно выбрать ее расчетную схему. Приведенное выше условное деление элементов на стержни, пластины и оболочки фактически является схематизацией их формы. Применяется также и схематизация свойств материалов. Упругость является реальным свойством большинства материалов в определенном диапазоне нагрузок и температур. Идеально упругие тела полностью возвращаются в исходное состояние после разгрузки. При больших нагрузках реальные материалы обнаруживают свойство пластичности, выражающееся в возникновении остаточных деформаций после устранения нагрузки. Для обоснования справедливости применения анализа явлений в пределах бесконечно малых объемов и последующего интегрирования все материалы считаются однородной, изотропной, сплошной средой. Изотропными являются материалы, имеющие одинаковые свойства по всем направления.

Принцип совместимости деформаций: под действием нагрузок тело деформируется так, что левая и правая части по поверхности воображаемого раздела полностью соответствуют друг другу по относительным перемещениям.

Гипотеза плоских сечений: сечения, плоские до деформации, остаются плоскими после деформации.

П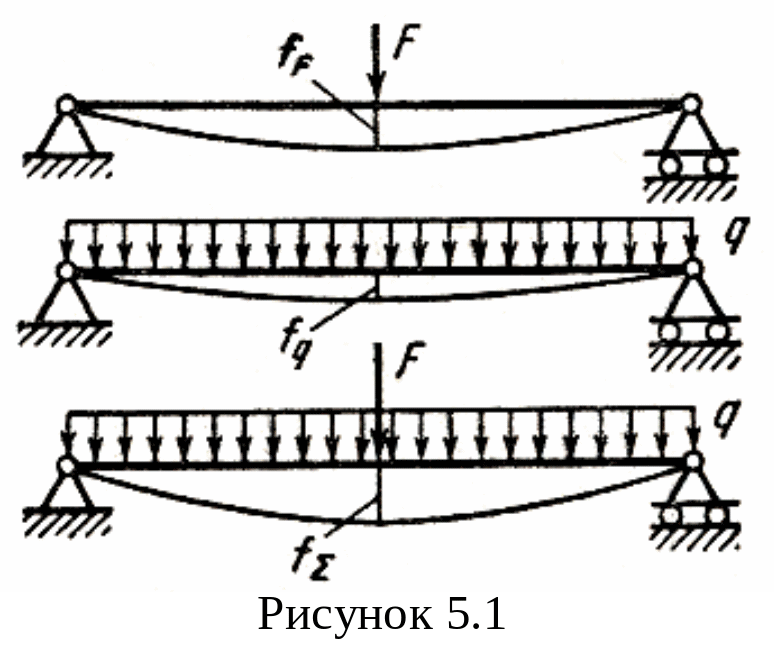 ри решении задач на конструкцию может действовать совокупность факторов. В этом случае для определения суммарного результата используется принцип суперпозиции или принцип независимости действия факторов: т.е. результат действия системы сил не зависит от порядка их приложения и равен сумме результатов действия отдельных сил, входящих в систему.

Пример: (рисунок 5.1).

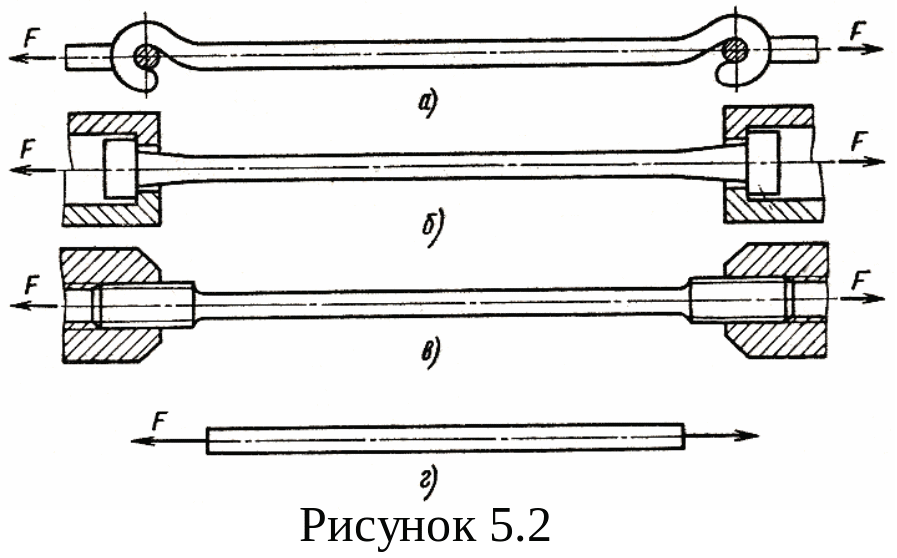
Принцип Сен-Венана: внутренние силы, достаточно удаленные от места действия внешних сил, не зависят от способа приложения внешней силы (рисунок 5.2).

3.1. Внутренние силовые факторы

К внутренним силам относят силы взаимодействия между отдельными частями рассматриваемого объекта. В расчетной практике силы обычно называют нагрузками. Действующие нагрузки делятся на сосредоточенные (сила F, момент М) и распределенные q. Статическими нагрузками считают нагрузки, медленно изменяющиеся во времени, их обычно принимают постоянными. Динамическими считают нагрузки, быстро меняющиеся во времени.

Не вдаваясь в детальный анализ процесса разрушения можно отметить, что разделение тела на части может произойти, если внутренние силы превзойдут силы сцепления отдельных частиц материала. Поэтому для суждения о прочности элемента необходимо сопоставлять максимальные внутренние усилия с предельными характеристиками для данного конструкционного материала. Для этого нужно знать закон изменения внутренних усилий по длине элемента.

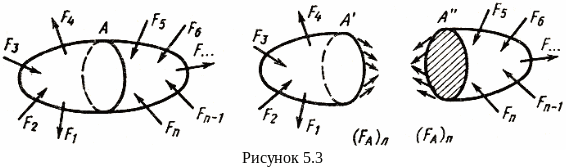
Внутренние усилия определяют методом сечений, который состоит в следующем: если тело находится в равновесии, то его левая и правая части относительно воображаемой поверхности раздела тоже находятся в равновесии (рисунок 5.3).

Условие равновесия тела:

.

Для обеспечения равновесия левой и правой частей на поверхности раздела необходимо приложить некоторую систему сил, дополняющую систему внешних сил до равновесной.

Условия равновесия левой и правой частей тела:

,

.

Из этих уравнений следует, что

.

Отсюда следует, что система внутренних является единственной и может определяться из условий равновесия как левой, так и правой части. Система внешних сил сводится к главному вектору R и главному моменту М. Система внутренних усилий R_вн и М_вн статическим им эквивалентна.

В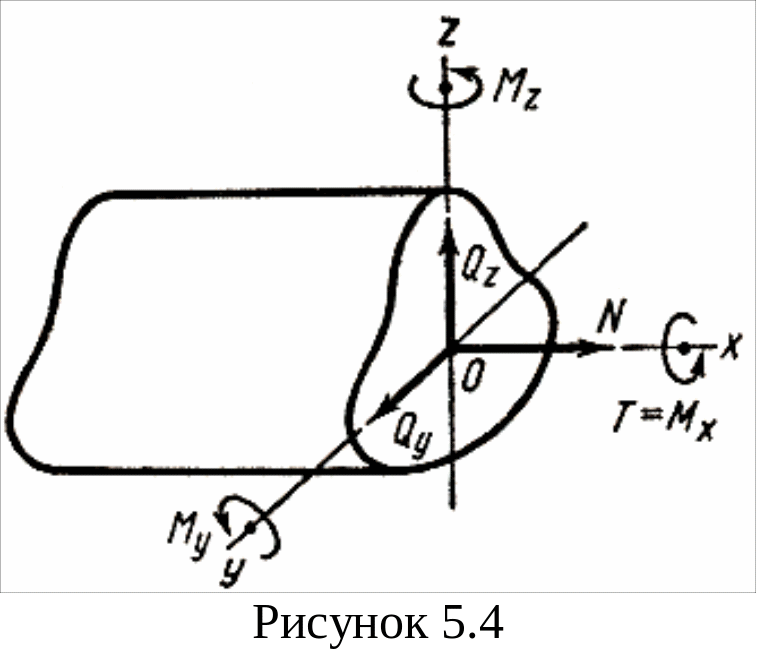 место отыскания векторов R и М удобно определять их проекции на оси координат. Начало системы координат совмещают с центром тяжести сечения (рисунок 5.4).

Усилия N, Q_y, Q_z, T, M_y, M_z называют силовыми факторами. Они определяются из 6 уравнений, вытекающих их условий равновесия:

Интенсивность внутренних усилий характеризуется величиной напряжения.

Допустим на тело действует некая система сил (рисунок 5.5). Рассмотрим в сечении А элементарную площадку . На нее действует сила .

Полным напряжением называется предел

.

Векторы и Р могут быть разложены на нормальную и тангенциальную составляющие. Таким образом, получается соответственно нормальное и касательное напряжения: и . Нормальное напряжение характеризует интенсивность отрыва или нажатия частиц материала, касательное – интенсивность относительно сдвига частиц.

Размерность , , .

По характеру создаваемой деформации силовые факторы называют осевой силой N, поперечными силами Q_y и Q_z, крутящим моментом T, изгибающими моментами M_y и M_z.

Графики, показывающие изменение силовых факторов по длине элемента, называют эпюрами. При построении эпюр принято правило знаков – рисунок 5.6.

18