Уравнение теплопроводности. Поток тепла. Коэффициенты теплопроводности и температуропроводности. Начальное условие часть 2. Тепломассообмен Тема 9. Теплопроводность

9.1.Основные понятия и определения

Теория теплопередачи, или теплообмена, представляет собой учение о процессах распространения теплоты в пространстве с неоднородным полем температур.

Существуют три основных вида теплообмена: теплопроводность, конвекция и тепловое излучение.

Теплопроводность — это молекулярный перенос теплоты между непосредственно соприкасающимися телами или частицами одного тела с различной температурой, при котором происходит обмен энергией движения структурных частиц (молекул, атомов, свободных электронов).

Конвекция осуществляется путем перемещения в пространстве не­равномерно нагретых объемов среды. При этом перенос теплоты не­разрывно связан с переносом самой среды.

Тепловое излучение характеризуется переносом энергии от одного тела к другому электромагнитными волнами.

Часто все способы переноса теплоты осуществляются совместно. Например, конвекция всегда сопровождается теплопроводностью, так как при этом неизбежно соприкосновение частиц, имеющих различные температуры.

Совместный процесс переноса теплоты конвекцией и теплопроводностью называется конвективным теплообменом. Частным случаем конвективного теплообмена является теплоотдача — конвективный теплообмен между твердой стенкой и движущейся средой. Теплоотдача может сопровождаться тепловым излучением. В этом случае перенос теплоты осуществляется одновременно теплопроводностью, конвекцией и тепловым излучением.

Многие процессы переноса теплоты сопровождаются переносом вещества — массообменном, который проявляется в установлении равновесной концентрации вещества.

Совместное протекание процессов теплообмена и массообменна называетсятепломассообменном.

Теплопроводность определяется тепловым движением микрочастиц тела. В чистом виде явление теплопроводности наблюдается в твердых телах, неподвижных газах и жидкостях при условии невозможности возникновения в них конвективных токов.

Передача теплоты теплопроводностью связана с наличием разности температур тела. Совокупность значений температур всех точек тела в данный момент времени называется температурным полем. В общем случае уравнение температурного поля имеет вид:

(9.1) где t — температура тела; х, у, z — координаты точки; τ — время. Такое температурное поле называется нестационарным и отвечает неустановившемуся режиму теплопроводности. Если температура тела не изменяется с течением времени, то температурное поле называется стационарным. Тогда

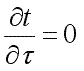, (9.2)

Температура может быть функцией одной, двух и трех координат, соответственно температурное поле будет одно-, дву- и трехмерным. Наиболее простой вид имеет уравнение одномерного стационарного температурного поля:

; ;

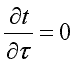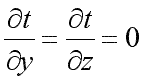
Если соединить все точки тела с одинаковой температурой, то получим поверхность равных температур, называемую изотермической. Так как в определенной точке тела в данный момент времени может быть только одна температура, изотермические поверхности не пересекаются; все они либо замыкаются на себя, либо заканчиваются на границе тела. Пересечение изотермных поверхностей плоскостью дает на ней семейство изотерм. Интенсивность изменения температуры в каком-либо направлении характеризуется производной  , принимающей наибольшее значение в направлении нормали к изотермической поверхности 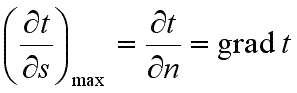(9.3)

Вектор   называется температурным градиентом и является мерой интенсивности изменения температуры в направлении по нормали к изотермной поверхности. Направлен он в сторону возрастания температуры.

9.2.Закон Фурье

Согласно гипотезе Фурье, количество теплоты d²Q_τ, проходящее через элемент изотермической поверхности dF за промежуток времени dτ, пропорционально температурному градиенту  : 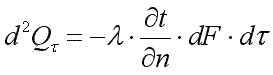(9.4)

Здесь множитель λ называется коэффициентом теплопроводности. Знак минус указывает на то, что теплота передается в направлении уменьшения температуры. Количество теплоты, прошедшее в единицу времени через единицу изотермической поверхности, называется плотностью теплового потока:

(9.5)

Проекции вектора q на координатные оси соответственно:

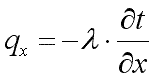
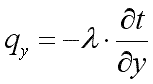
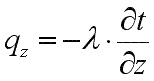
Уравнения (9.4) и (9.5) являются математическим выражением основного закона теплопроводности — закона Фурье.

Количество теплоты, проходящее в единицу времени через изотермическую поверхность F, называется тепловым потоком: 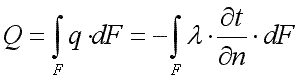(9.6)

Полное количество теплоты, прошедшее через эту поверхность за время τ, определится из уравнения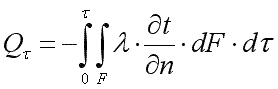 (9.7)