§5 Системы линейных алгебраических уравнений.
Опр.1 Системой из m лин. ур-й с n неизв. наз. сист. вида:
(1),
-коэф.
при неиз-х
,
-
свобод. коэф.,
,
n – число неиз-х, m – число ур-й.
Опр.2
Система (1)
наз. однородной
при
,
.
Опр.3
Упорядоченная
система чисел
наз. решением
сист. (1), если при подстановки этих чисел
вместо неиз-х в сист. каждое ур. обращ-ся
в верное рав-во.
Опр.4 Две системы наз. эквивалентными или равнос-ми, если всякое решение одной яв-ся решением другой.
Опр.5 Элемент-ми преобразованиями сист.(1) наз. след.
прибавление к ур-ю др. ур., умнож. на к-л число;
умножение к-л ур. на число отличное от нуля;
перестановка местами ур-й системы.
Т. Элем. преоб. системы.. приводят ее к эквивалентной.
Опр.6 Система (1) наз. совместной, если она имеет хотя бы одно решение (в противном сл. - несовместной).
Опр.7 Система (1) наз. определенной, если имеет ед. реш., неопределенной, если имеет б. мн-во решений.
§ 6 Методы решения систем линейных уравнений.
6.1.Матричный метод
Для системы (1) при m=n введем обозначения:
-
м-ца из коэф. при неизвестных, причем
,
т.е. м-ца А –
невырожденная,
,
,где
X
– м-ца столбец из неизвестных, B–м-ца
столбец из свободных коэффициентов.
Тогда (1) можно записать матричным
уравнением:
(2) – матричная
запись системы
из n
лин. ур-й с n
неизв-ми.
Решим
(2):
.
_________________________________________________________
ПР.
нев.
; (см. §3),
,
,
=
,
.
6.2. Метод Крамера.
Для
(1) при условии m=n
и
введем обозначения:
- определитель
системы,
,…,
.
Тогда
м. док-ть, что
(3)- фор-лы Крамера.
Если , сист. имеет ед. решение;
Если
и
хотя бы один из
,
сист. не имеет реш.
Если
и
все
,
то сист. имеет беск. мн-во реш., к-е
м.
найти с помощью метода Гаусса.
ПР. -невырожд.
=-13;
,
,
.
Проверка.
6.3 Метод Гаусса.
Опр.1
Базисными неизвестными
сист. (1) назовем любые ее r
неизвестных,
,
коэффициенты при к-х образуют базисный
минор; свободными неизвестными назовем
остальные (n-r)
неизвестные.
Т. Кронекера – Капелли
Для совместности системы (1) необходимо и достаточно, чтобы ранг м-цы системы был равен рангу ее расширенной матрицы, т.е. м-цы, полученной из м-цы сист. добавлением столбца из свободных коэффициентов.
Т.о.
(1) совместна
,
при этом:
если r = n, то (1) имеет ед. решение;
если r<n, то (1) имеет бесконечное мн-во решений.
C помощью эл. преоб. сист. ур-ий ее м. привести к экв-ной системе: а) трапециевидной формы в случае, если m<n; б) треугольной формы в случае, когда m=n. (илл. на примере). Обе сист легко решаются методом послед-ного исключ. неиз-ых, начиная с последнего ур-ия.
Т. к. эл. преоб. сист. ур-й аналогичны эл. преоб. над строками ее расш-й м-цы, то, сл-но, м. работать с расш-й м-цей: с помощью эл. преоб.; привести ее к трапец-й форме (или к треуг.); опр-ть ранг расш. м-цы и м-цы сист.; на основании т. К-К сделать вывод о совместности сист.
_________________________________________________________
Если
сист. совместна, т. е.
,
выделяем бази-й минор
и бази-ые неизв-е(r
штук), заменяем сист. на экв-ую, состоящую
из r
ур-ий, в к-ые вошли элементы баз. минора;
экв. сист. решаем послед исключ. неизв.
В случае, кода
баз. неиз-ные выражаем ч/з свобод.,
придавая свободным неиз-ым произвольные
значения, получаем бесконечное множество
решений.
Метод решения систем ур-й вида (1), основанный на использовании эл. преобр. систем, имеет название м-да Гаусса или м-да исключений.
ПР.
=
.
сист.
совместна;
сист.
имеет б.м.р.;
,
-
баз. неиз.,
-св.н.
По виду составляем сист. эквивалентную данной:
ПР.
Система лин. алг. одн. ур.
=
.
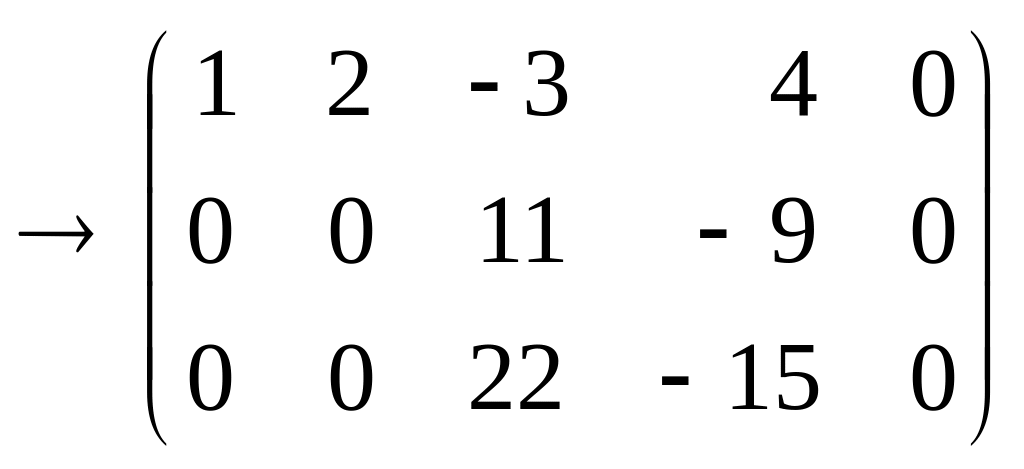
сист. совм. и имеет б.м.р.
ПР.
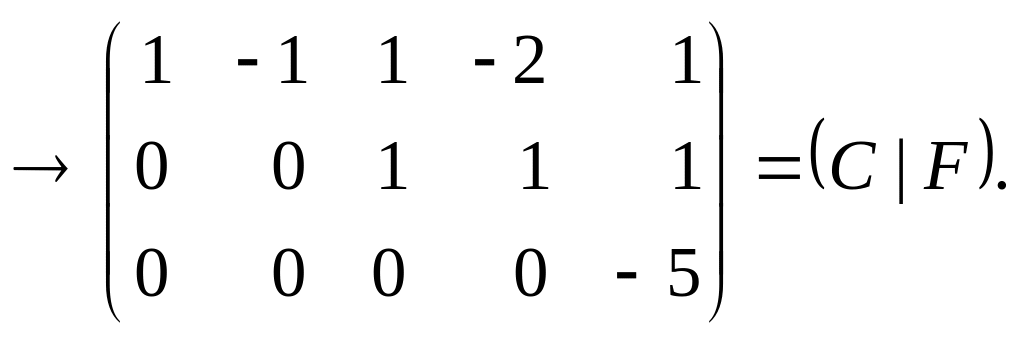
система несовместна, т. е. не имеет решения.