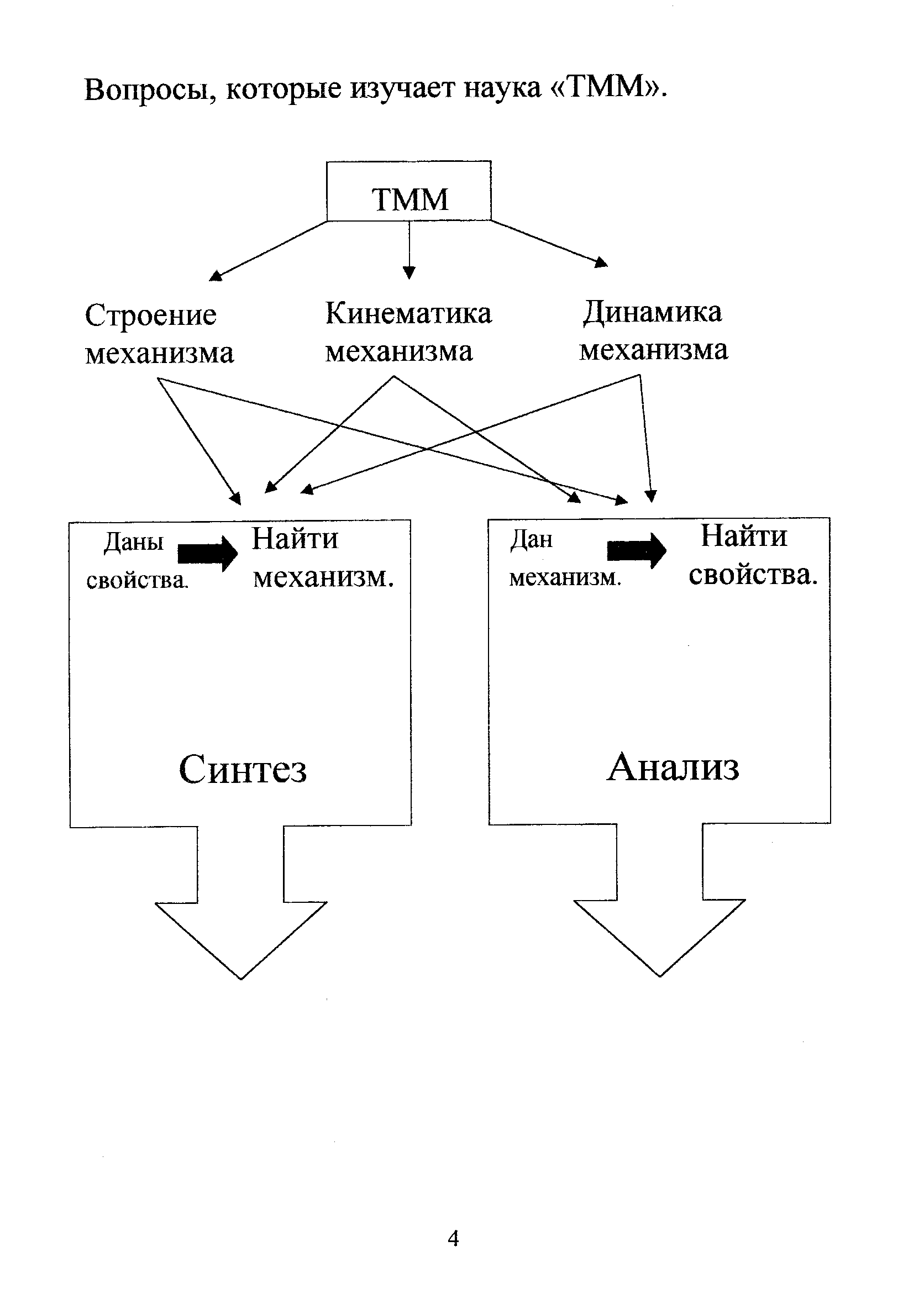
Простейшие четырехзвенные плоские механизмы состоят из одного неподвижного звена (стойка) и трех подвижных звеьев.

Если все пары вращательные, то механизм называется шарнирным четырехзвенником. Звено которое совершает полный оборот вокруг оси вращения, называется кривошипом.

Звено которое совершает непольный оборот вокруг оси вращения, называют коромыслом.

Звено совершающее плоскопараллельное движение, называются шатуном.

Если звено 3 соединить состойкой поступательной парой, то оно будет называться ползуном, а вес механизм – кривошипно-ползунным. Втом случае, если поступательная пара находится между звеньями 2 и3 , т.е. звено 2 пермещается по подвижной направляющей, механизм называется кулисным.

Если коромысло служит подвижной направлящей для ползуна, то называют кулисной , а ползун-кулисном каменем.

Тема2. Структурный синтез и анализ механизмов. Формула строение

механизма.

2.1. Основные понятия и определения строения механизмов

Всякий механизм состоит из отдельных деталей (тел). Некоторые детали являются неподвижными, другие детали движутся относительно их. Одну жесткую деталь или несколько неподвижно соединенных между собой деталей называют звеном механизма. В свою очередь, звенья механизма могут быть подвижными и неподвижными. Неподвижное звено называется стойкой. Обычно за стойку принимают корпус или раму машины, а так же все жестко связанные с ними деталей. Стойка в механизме всегда только одна [1].

Звенья, имеющие возможность относительно перемещения, называют относительно подвижными. Подвижные звенья бывают входными (ведущими) и выходными (ведомыми). Звено, которому сообщается движение, называют входным. Звено, которое осуществляет требуемое движение, для которого предназначен механизм, называется выходным.

В теории механизмов часто пользуются понятием начального звена. Начальным называют звено, координаты которого являются обобщенными для данного механизма, т.е. определяют движение остальных звеньев. Чаще всего за начальное звено принимают входное звено, однако не всегда эти понятия совпадают.

Поверхности, линии, точки звена, по которым оно соприкасается с другим звеном, называют элементами звена [1].

Подвижное соединение двух соприкасающихся звеньев называют кинематической парой. Для существования кинематической пары необходимы 3 условия:

- наличие двух звеньев;

- постоянное соприкосновение этих звеньев;

- возможность их относительного перемещения.

Для того, чтобы элементы кинематической пары находились в постоянном соприкосновении, необходимо обеспечить замыкание пары – геометрическое (за счет конструктивной формы звеньев) либо (силой тяжести, пружиной, давлением газа или жидкости).

Кинематические пары во многом определяют работоспособность машины, поскольку через них передаются усилия от одного звена к другому, вследствие трения элементы пары находятся в напряженном состоянии и подвергаются износу. Поэтому правильный набор вида кинематической пары, ее геометрической формы, размеров, конструкционных материалов и смазки имеет важное значение при проектировании механизма.

Система звеньев, связанных между собой кинематическими парами, называется кинематической цепью. Например, в механизме двигателя внутреннего сгорания коленчатый вал образует с неподвижным подшипником кинематическую пару (соединение, допускающее возможность относительного движения). Шатун с коленчатым валом образует вторую кинематическую пару, поршень с шатуном – третью, поршень и цилиндр – четвертую, а совокупность кинематических пар составляет кинематическую цепь [3].

Таким образом, в основе всякого механизма лежит кинематическая цепь. Но не всякая кинематическая цепь представляет собой механизм, а только та, звенья которой осуществляют заданные движения.

2.2. Кинематические пары и их классификация

Кинематические пары (КП) классифицируются по следующим признакам:

1. По виду места контакта (места связи) поверхностей звеньев:

- низшие, в которых контакт звеньев осуществляется по плоскости или поверхности (пары скольжения);

- высшие, в которых контакт звеньев осуществляется по линиям или точкам (пары, допускающие скольжение с перекатыванием).

2. По относительному движению звеньев, образующих пару:

- вращательные;

- поступательные;

- винтовые;

- плоские;

- сферические.

3. По способу замыкания (обеспечения контакта звеньев пары):

- силовые (за счет действия силы веса или силы упругости пружины);

- геометрическое (за счет конструкции рабочих поверхностей пары).

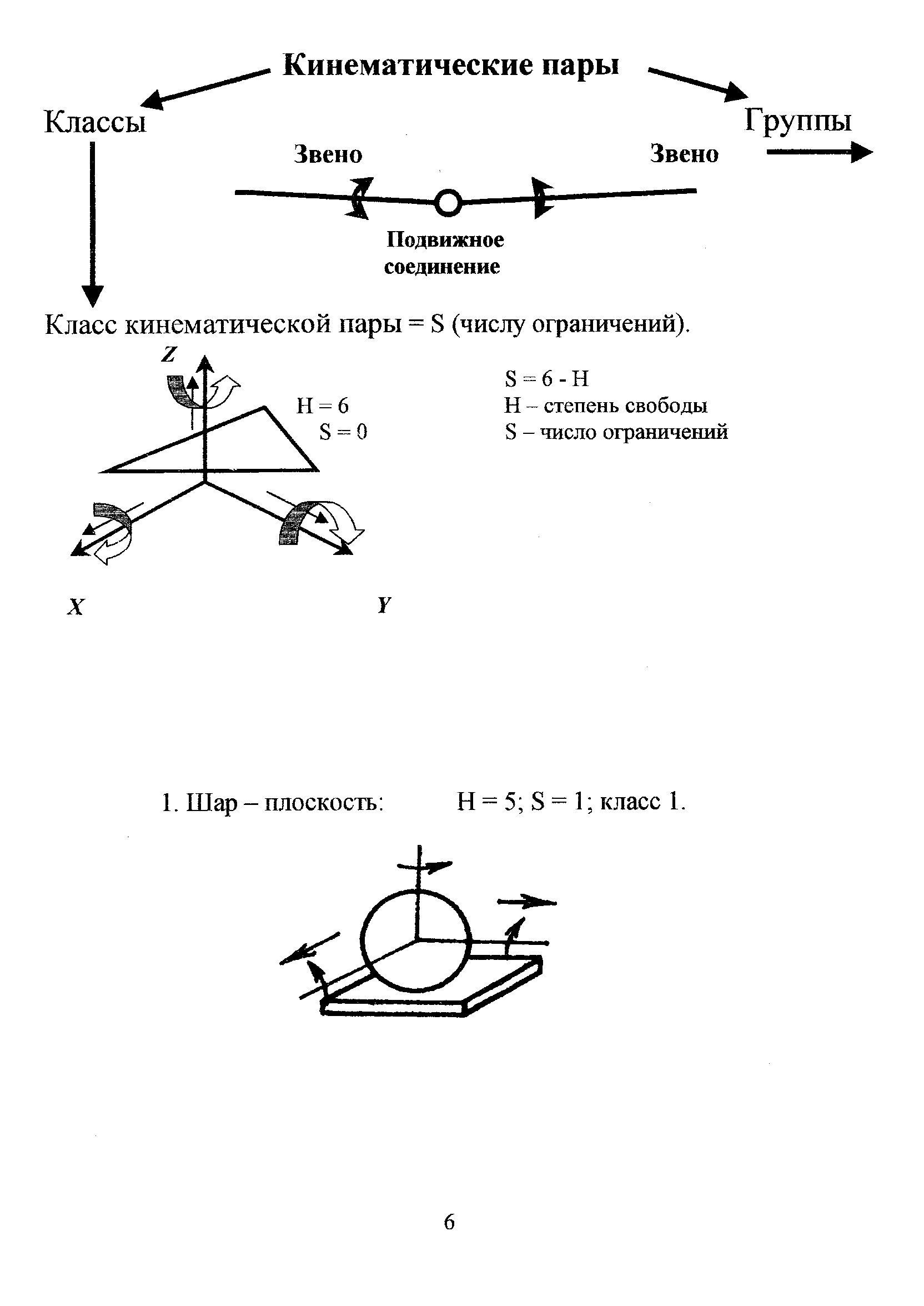
4. По числу условий связи, накладываемых на относительное движение звеньев (число условий связи определяет класс кинематической пары).

5. По числу подвижностей в относительном движении звеньев.

Подробнее рассмотрим классификацию кинематических пар по числу условий связи и числу подвижностей в относительном движении звеньев. Возможные соединения звеньев в кинематические пары весьма разнообразны, в связи, с чем ограничивается подвижность звеньев в той или иной степени.

Всякое тело, свободно движущееся в пространстве, обладает шестью степенями свободы, т.е. движение может быть представлено как вращение вокруг трех осей и поступательное движение вдоль этих же осей.

Если звено не входит в кинематическую пару, т.е. не связано с другим звеном, то у него нет никаких ограничений движению: S = 0, где S – число условий связи.

Если наложить 6 связей, то звенья теряют относительную подвижность и получается жесткое соединение, т.е. кинематической пары не станет (нет относительного движения звеньев): S = 6.

Следовательно, число условий связи, наложенных на относительное движение звеньев, находится в пределах:

1 ≤S ≤5.

Неравенство справедливо для звена, входящего в кинематическую пару.

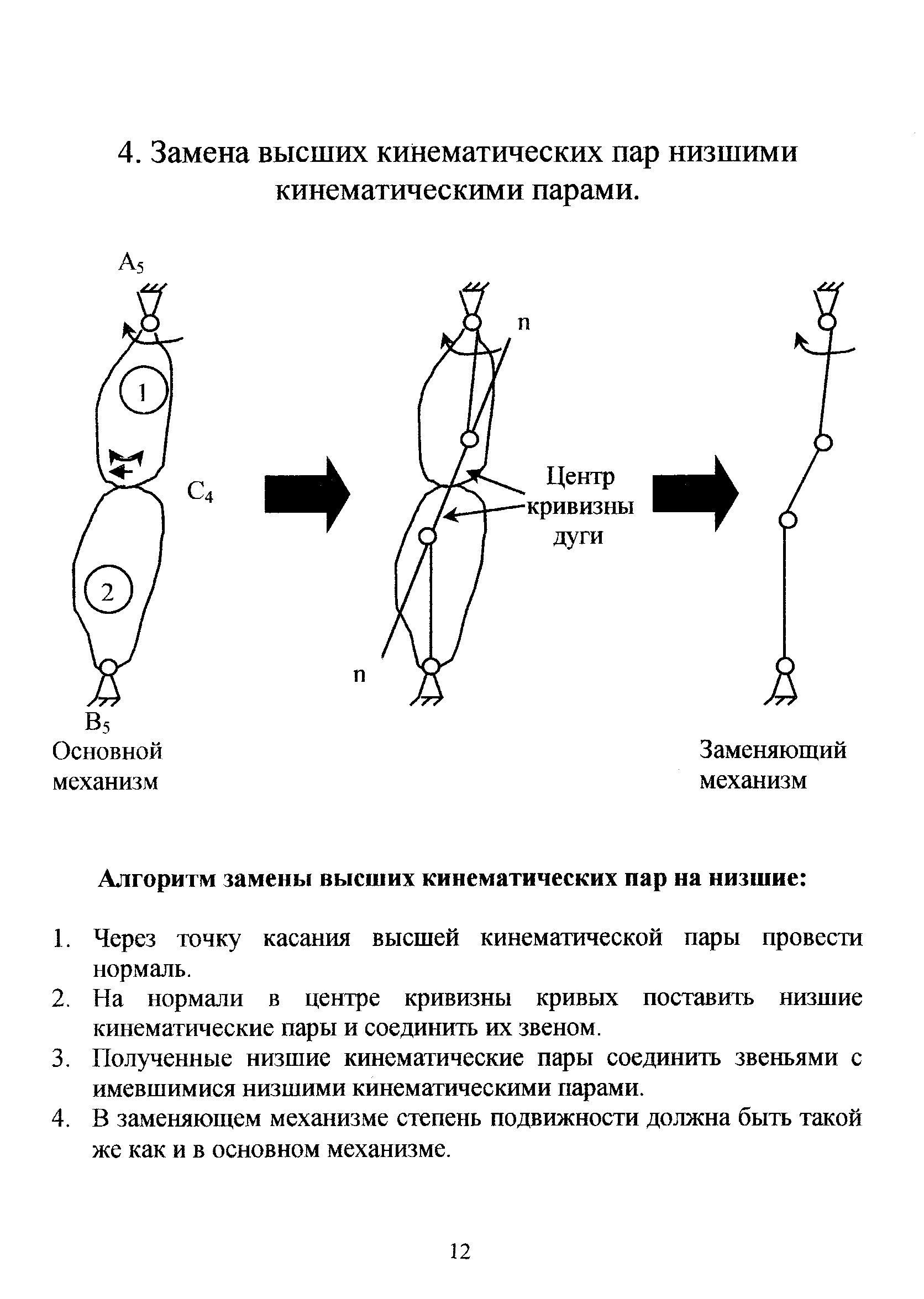
Поскольку число связей меняется от 1 до 5, существует 5 классов кинематических пар. В зависимости от вида элементов, по которым соприкасаются кинематические пары, различают высшие и низшие кинематические пары. К высшим относятся пары, звенья в которых соприкасаются по линиям или в точке. К низшим относятся пары, у которых звенья соприкасаются по поверхностям.

Все пары 5-го класса – низшие (поступательная, вращательная, винтовая). Пары 4-го класса бывают как высшими, так и низшими. Например, зубчатое зацепление, кулачок с толкателем представляют собой высшие пары (звенья соприкасаются в точке), а цилиндрическая пара – 4-го класса, но это уже пара низшая, т.к. контакт между звеньями проходит по поверхности.

К низшим парам кроме уже упомянутых относятся также сферический шарнир – пара 3-го класса, сферический шарнир с пальцем – пара 4-го класса, плоскостная пара – пара 3-го класса.

1.6 Кинематическая цепь. Структурная формула кинематической цепи

Кинематическая цепь – это система звеньев, образующих между собой кинематические пары. Кинематические цепи различают по следующим признакам:

а) замкнутые и незамкнутые;

б) простые и сложные;

в) плоские и пространственные.

В замкнутой цепи каждое звено входит не менее чем в две кинематические пары; в незамкнутой есть звенья, входящие только в одну кинематическую пару.

В простой цепи каждое звено входит не более чем в две кинематические пары; в сложной цепи есть звенья, входящие более чем в две кинематические пары.

В плоской цепи все звенья перемещаются в одной плоскости либо в параллельных плоскостях; в пространственной – звенья движутся в разных, непараллельных плоскостях.

Структурная формула кинематической цепи связывает число степеней свободы (т.е. число независимых движений) с числом и видом кинематических пар в данной кинематической цепи.

Пусть в механизме имеется k звеньев (включая стойку). Каждое звено до соединения его с другим звеном имеет в пространстве 6 степеней свободы кинематической цепи равно 6k.

Соединение звеньев в кинематические пары накладывает определенное число связей, которые надо исключить из общего числа степеней свободы.

Учитывая, что каждая пара 5-г класса накладывает 5 связей, пара 4-го класса – 4 связи и т.д., число степеней свободы кинематической цепи Н в общем случае определяется соотношением:

H = 6k – 5P₅ – 4P₄ – 3P₃ – 2P₂ – P₁,

(1.1)

Где P₅, P₄, P₃, P₂, P₁ – число кинематических пар 5-го, 4-го…1-го класса.

Если рассматривать движение механизма относительно стойки (неподвижного звена), то из общего количества звеньев надо вычесть это звено:

n = k – 1,

(1.2)

где n – число подвижных звеньев в кинематической цепи.

Степень подвижности механизма (W) относительно стойки определяется по формуле:

W = 6n – 5P₅ – 4P₄ – 3P₃ – 2P₂ – P₁.

(1.3)

Полученная формула называется структурной формулой кинематической цепи и носит имя А.П.Малышева. Формулу (3) можно представить и в более компактном виде:

₅

W = 6n – Σ iP_i

^{i = 1}

(1.4)