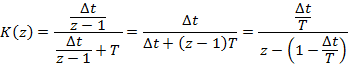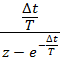Численное решение нелинейных ду

Рассмотрим на основе НДУ 1-ого порядка

Численное решение позволяет в какой-либо момент времени найти выходное значение по значению входного процесса в этот момент и выходной в предыдущий момент.

Ч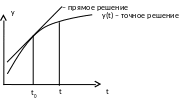 исленное решение основано на использовании разложения в ряд Тейлора.

Ограничимся 2 первыми членами. Обозначим t₀=t_k-1, t=t_k, t-t₀=∆t – интервал дискретизации.

– выражение для расчета прямым методом Эйлера

Рассмотрим обратный метод Эйлера t₀=t_k, t=t_k-1

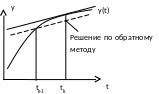
– обратный метод Эйлера

Недостатком вычисления по обратному методу Эйлера является неявная зависимость y_k от x_k и y_k-1.

Можно уменьшить ошибку вычисления, если усреднить решение по прямому и обратному методам Эйлера.

– метод трапеций.

Метод Рунге-Кутта 2-ого порядка:

Более высокую точность имеет метод Рунге-Кутта порядка выше второго.

Метод Рунге-Кутта 4-ого порядка:

М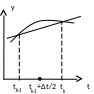 етод Рунге-Кутта 4-ого порядка – уточнение угла наклона экстраполирующей прямой – производится по расчету в промежуточной точке в середине интервала ∆t.

Р асчет выходного процесса линейной системы с использованием интеграла свертки

Перейдем к дискретному времени: t=n∆t

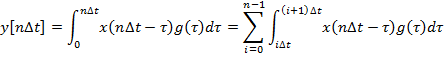
И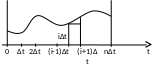 спользуем ступенчатую аппроксимацию входного процесса:

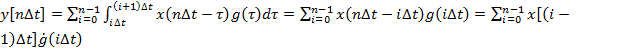
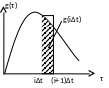
Таким образом, весовые коэффициенты представляют собой по смыслу площадь под импульсной характеристикой за интервал дискретизации ∆t.

Если ∆t мал, то можно использовать ступенчатую экстраполяцию импульсной характеристики g(τ).

Когда интервал дискретизации мал, то для уменьшения машинного времени можно перейти от большого количества слагаемых к рекуррентной формуле, которая позволяет найти выходной процесс через предыдущие значения выходного процесса.

Переход от непрерывной передаточной функции к дискретной

Воспользуемся дискретизацией импульсной характеристики

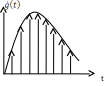
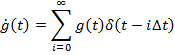
– дискретное преобразование Лапласа (ДПЛ).

Если e^-p∆t = z → z-преобразование

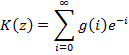
K(p)	K(z)
Интегрирующее звено
Инерционное звено

Разностное уравнение

(z-1)Y(z)=zX(z)

y[n+1]-y[n]=x[n+1]

y[n+1]=y[n]+x[n+1]

В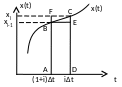 озможен переход к дискретной переходной функции с использованием формул численного интегрирования и заменой в передаточной функции операций аналогового интегрирования дискретным.

y_i=y_i-1+S_ABCD

Приближенные методы

1. Метод прямоугольников 1

y_i=y_i-1+∆t∙x_i-1

z-преобразование

Y(z)=z^-1Y(z) +∆t∙z^-1X(z)

Y(z)(1-z^-1)= ∆t∙z^-1X(z)

2. Метод прямоугольников 2

y_i=y_i-1+∆t∙x_i

Y(z)=z^-1Y(z) +∆t∙X(z)

3. Метод трапеций

y_i=y_i-1+S_{трап ABCD} = y_i-1+∆t(x_i-1+x_i)/2

Z:

K(p)	K(z)
	Прямоуг 1	Прямоуг 2	Трапеций

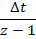
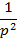
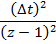
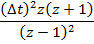
Операция по последовательному соединению интеграторов не соответствует операции последовательного соединения дискретных интеграторов.

Переход от непрерывной передаточной функции к дискретной совершается следующим образом: числитель и знаменатель непрерывной передаточной функции делится на p в высшей степени полинома знаменателя. В полученном выражении 1/p в соответствии степени знаменателя операцией дискретного интегрирования.

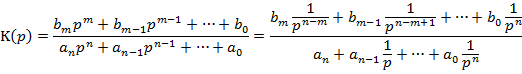
Например: моделирование интегрирующей цепи:
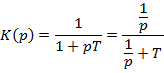