Восстановление сигнала по его дискретным отсчетам с использованием фиксаторов нулевого и 1-ого порядка

Ф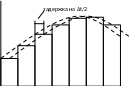 иксатор нулевого порядка преобразует отсчеты входного процесса, запоминая значения процесса на последующий интервал дискретизации.

Экстраполяция значения процесса на интервале дискретизации.

С равним фиксатор нулевого порядка с идеальным восстанавливающим фильтром.

Комплексная частотная характеристика

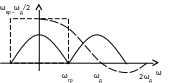
Фиксатор нулевого порядка будет хуже идеального восстанавливающего фильтра, т.к.:

1. В пределах ±ω_гр коэффициент передачи фиксатора нулевого порядка меньше единицы и изменяется по частоте

2. За пределами полосы пропускания идеального фильтра

|ω|>ω_гр коэффициент передачи отличен от нуля.

Тем самым оказывается подчеркнутыми ВЧ составляющие не входящие в спектр частотного сигнала. Нужно повышать U_д, чтобы уменьшить эти ошибки.

ω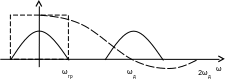 _гр=ω_д/4, т.е. ω_д=4ω_гр

Видим, что коэффициент передачи фиксатора в пределах |ω|<ω_гр приближается к единице, а в диапазоне ω>ω_гр появились свободные от спектра участки, и значит, уменьшились ВЧ искажения.

При моделировании берется ω_д 3-5 (2ω_гр)

П ри установлении фиксатора 1-ого порядка осуществляется линейная интерполяция задержания на интервал дискретизации.

И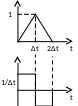 мпульсная характеристика

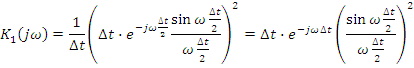
С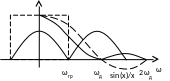 равним 1-ого порядка и идеального

Использование фиксатора 1-ого порядка приводит к значительному падению ВЧ составляющих на |ω|>ω_гр. Хотя отличие АЧХ от 1 в области частот |ω|<ω_гр стало больше.

Но главный недостаток фиксатора 1-ого порядка является задержка установления сигнала на интервале дискретизации, поэтому при моделировании такой фиксатор используется редко.

Математические схемы моделей

–входное воздействие

–мешающее воздействие

– выходное воздействие

– внутренние характеристики системы

- закон функционирования системы

Закон функционирования системы может записываться в виде дифференциального, интегрированных, логически уравнений, алгоритмов в зависимости от типа системы и характера процесса в этой системе.

Характер процессов	Тип системы
Непрерывные	Детерминированные структуры
дискретные	С вероятностной структурой

1 схема: непрерывно – детерминированная

Эта схема используется для описания динамических систем (в которых выходные процессы запаздывают).

d–схема (dynamic system)

математическое описание:

• Дифференциальное уравнение

• Интегрированное уравнение

2 схема: дискретно-детерминированная

Используется для математического описания дискретных и цифровых устройств, которые относятся к классу конечных автоматов.

Конечный автомат характеризуется конечным набором входных и выходных значений (конечным алфавитом).

Сам автомат представляет собой цифровую схему:

• Б ез памяти – комбинационные схемы

• С памятью – комбинационная схема + триггеры

Для определения связи выходных и входных величин требуется знать внутреннее состояние системы – Z.

Эти переменные связаны между собой функцией перехода и функцией выхода.

Z_k+1=ϕ(Z_k,X_k) – функция перехода

Z_k=ψ(Z_k,X_k) – функция выхода

Математическим описанием является система логических уравнений.

Схема называется f-схема (finite automat)

F=<x, y, z₀, z, ϕ(z,x), ψ(z,x)>

3 схема: дискретно-стохастическая

Используется для вероятностных автоматов (probability automat).

p-схема.

В отличии от конечного автомата, определяющего входной сигнал и состояние системы может соответствовать несколько выходных сигналов, каждый со своей вероятностью появления.

Поэтому вместо функции входа и выхода используется матрица вероятности перехода, из состояния z_k, x_kв состояние z_k+1, y_k.

В-матрица вероятностей перехода-выхода.

P=<x, y, z₀, z, B>

4 схема: g-схема.

Д ля описания систем массового обслуживания.

Д ля математического описания сложных систем, к которым не подходит не одна из этих схем, используется А-схема (агрегативная схема).

Математическая модель по d-схеме

1. Непрерывные системы осуществляют как линейную так и нелинейную обработку, если обработки нельзя разделить, то единственное математическим описанием является нелинейное ДУ.

2. Если же можно разделить нелинейную и линейную обработку, то модель становится более простой, состоящей из нелинейных блоков, описываемых y=f(x)

и линейных блоков, которые описываются линейным ДУ или связанным с ними другого вида математического описания

В екторно-матричная форма записи

Передаточная функция:

Комплексная частотная характеристика:

Временные характеристики:

• импульсная

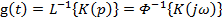
• переходная

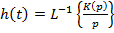
При моделировании линейных систем можно использовать как частотный метод вычисления, так и временной.

Частотный метод:

– метод установившихся процессов

Временной метод:

y – для расчета переходных процессов

y – установившейся процесс