Генерирование последовательностей со случайной зависимостью

(x₁, x₂, … x_n) – n-мерная случайная величина

n-мерная плотность распределения:

W(x₁, x₂, …x_n)= W(x₁)W(x₂/x₁)W(x₃/x₂,x₁)…W(x_n/x₁,x₂,…x_n-1)

Генерирование случайной последовательности – сложно, используют другие более простые алгоритмы.

1. Основан на простой цепи Маркова (цепь 1-ого порядка).

2. Основан на спектрально-корреляционной теории.

При этой теории вместо n-мерной плотности распределения используется двумерная

W(x_k, x_l)

K и l – любые числа от 1 до n.

Используется второй смешанный момент двумерной плотности распределения.

Корреляционный момент.

При использовании данного метода, зависимые случайные величины получаются в результате прохождения независимых случайных величин через линейные цепи.

Генерирование корреляционных случайных процессов методом фильтрации

x (t) – независимый случайный процесс(СП) (Белый шум).

Его корреляционная функция:

; δ – символ Кронекера

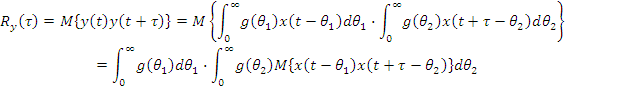
Автокорреляционная функция выходного процесса с точностью до постоянного коэффициента σ_x² совпадает с автоковариационной функцией импульсной характеристики фильтра.

И спользуются цифровые фильтры

∆t – интервал дискретизации

Метод скользящего суммирования

x[n∆t]→x_n

Отсчет входного процесса

x₁, x₂, x₃, x₄, x₅, x₆, x₇

y₃= x₁+x₂+x₃

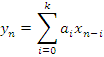
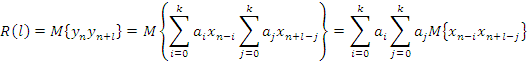
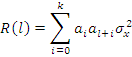
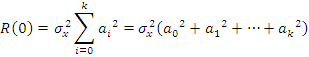
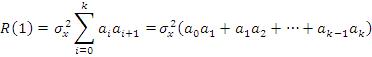
Этот метод используется, для генерирования случайного процесса с корреляционной функцией, ограниченной по времени.

П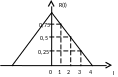 ример:

Найти a₀, a₁, a₂, a₃

Составим систему уравнений:

Для изображений используем Z-преобразование

Е сли требуется сгенерировать случайный процесс, у которого корреляционная функция имеет бесконечную протяженность по времени, то используют рекурсивный фильтры, простейший из которых авторегрессионный фильтр.

Это рекурсивный фильтр.

Р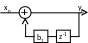 ассмотрим частный пример АР-фильтра 1-ого порядка.

Импульсную характеристику можно построить непосредственно, как реакцию фильтра на единичный фильтр.

Найдем корреляционную функцию переходного процесса как ковариационную функцию импульсных характеристик.

В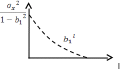 ыбор b₁ ограничен требованиями устойчивости фильтра, согласно правилу устойчивости дискретных систем корни знаменателя передаточной функции должны находиться внутри окружности с радиусом 1.

z- b₁=0 → z= b₁→ | b₁|<1 → -1<b₁<1

Фильтр 1-ого порядка позволяет генерировать случайные процессы с автокорреляционной функцией 2 типов:

1. М 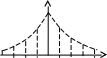онотонноспадающей 0<b<1

2. К олебательной -1<b<0

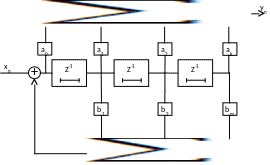
Больший выбор типов корреляционной функции будет, если взять АР-фильтр 2-ого порядка, который позволяет получить корреляционные функции колебательные с регулируемым периодом и скоростью спадания.

Еще большее разнообразие АКФ можно получить, используя АРСС-фильтр – авторегрессионный и скользящего среднего.

Дискретизация непрерывных процессов

Д искретизация происходит без потери информации, если состав дискриминатора выбирается по Котельникову и спектр сигнала ограничен ω_ср, тогда: ω_д≥2ω_гр

Ошибки в восстановлении процесса по его дискретным отсчетам связаны с 2 причинами:

1. Потери ВЧ составляющих, частоты которых больше ω_ср/2.

2. Добавление ВЧ составляющих, которые являются перевернутым спектром от ω_ср/2 до ω_гр.

При правильном выборе ω_д≥2ω_ср, эти ошибки устраняются.

Р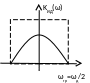 ассмотрим восстановление сигнала идеальным фильтром с прямоугольной характеристикой.

K_ид(jω)=1

Реально фильтр с АЧХ близкой к прямоугольной можно реализовать фильтр любого типа высокого порядка (Чебышева, эллиптический и др.)

φ (ω) – близка к линейной

Импульсная характеристика идеального ВЧ фильтра

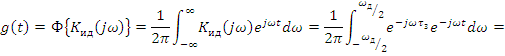
Таким образом, с точностью до постоянного множителя импульсная характеристика совпадает с функцией sin(x)/x.

Импульсная характеристика такого типа соответствует физически нереализуемой системе, так как импульсный отклик появляется до подачи импульса на вход, и для ид. Распространения требуется бесконечно большое время задержки.