Оценка законов распределения

Оценка законов распределения CВ производится по гистограмме распределения.

Гистограмма распределения – это столбиковая диаграмма показывающая вероятность попадания СВ в некоторую область:

1. Разбить весь интервал значений СВ на n подынтервалов (разрядов)

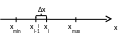Пусть k интервалов

2. Производится N испытаний в результате которых формируется массив из к значений.

3. Определяется количество испытаний n_i, в результате которых СВ попадает в i-й интервал.

4. Находятся оценки вероятности попаданий CВ в i-интервал.

О ценим плотность распределения СВ

Оценка функции распределения

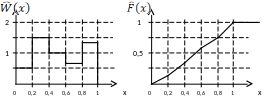
Оценка близости законов распределения генерируемой св к требуемому закону распределения

Наиболее известными критериями являются:

1. χ² - Пирсона

2. Колмогорова

Оценка близости по критерию χ ² - Пирсона производится по величине взвешенной функции квадратичного отклонения плотности распределения СВ и ее оценки.

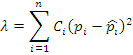
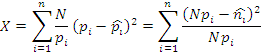
– теоретическое количество попаданий СВ в заданный интервал.

Пирсон доказал, что сумма из n случайных независимых величин, распределяется одинаково, имеет функцию распределения типа χ², которая зависит от числа степеней свободы k=n-s, где n–количество суммируемых величин (здесь – количество разрядов), s–количество независимых условий, накидываемых на n_i.

Например:

Д алее определяется вероятность того, что мера отличия λ будет не меньше значения, определяемого случайным характером измерений.

По этой характеристике, для рассчитанного λ, находят значение P(λ). Если P(λ) достаточно большое (P(λ)>0,1), считают, что гипотеза о близости закона распределения может быть принята.

Критерий Колмогорова

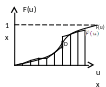
Критерий требует сравнения не плотностей вероятности, а функции распределения.

D – максимальное отличие.

Колмогоров показал, что максимальное отличие (D) функции распределения и ее оценки имеет закон распределения не зависящий от закона распределения случайной величины u, и поэтому можно оценить близость закона распределения по максимальному D.

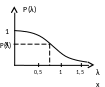
Если P(λ)>0,1, то гипотеза о близости законов распределения может быть принята.

Эти критерии по-разному учитывают значимость распределений в центре и по краям. Если необходимо учитывать с большим весом отличия на краях используют χ² – Пирсона. Различие в центре распределения – критерий Колмогорова.

Проверка независимости генерируемых св

Двумерная плотность вероятности W(U₁, U₂)=W(U₁)∙W(U₂/U₁)

U₁и U₂ независимы, если их плотности распределения вероятности не зависят друг от друга: W(U₁, U₂)=W(U₁)∙W(U₂)

Э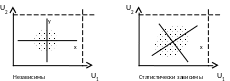 кспериментально независимость случайных величин можно определить по двумерному распределению, когда на осях откладываются случайные величины.

Наблюдаемые величины независимы, если изображения совместного распределения симметричны относительно осей параллельных осям U₁и U₂. Если оси симметрии наклонены, то случайные величины U₁и U₂ статически не зависимы.

Для количественной оценки используют несколько разновидностей методов серии.

Нужно определить независимость отсчетов СВ.

1. Переводится в последовательность нулей и единиц.

2. Находится вероятность превышения СВ U уровня U₀.

; n₀ – количество превышающих U₀.

Серия – последовательность одинаковых значений.

Доказано, что количество серий для независимой последовательности подчиняется нормальному закону распределения, мат ожидание и дисперсия, которых зависят от числа элементов N и вероятности превышения порога.

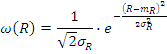
Находится минимальное и максимальное значение количества серий R_min и R_max из условия, что вероятность выхода количества серий за эти рамки будет меньше 2ε.

;

Если найденное количество серий находится в пределах R_min и R_max, то последовательность значений случайной величины считается независимой.

Метод длины серий.

С троится оценка вероятности того, что серия имеет определенную длину.

Теоретически распределение длины подчиняется закону Бернулли.

n_i – длина серии

N – длина последовательности