Алгоритмические датчики случайных чисел

Первый метод формирования был предложен Нейманом.

В ыделение середины квадрата числа

Недостаток – вырождение в 0.

Выделение середины квадрата произведения чисел

В современных ЭВМ используют датчики, основанные на линейной операции.

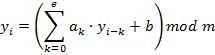
a, b – большие числа

Пример (10028) mod 10

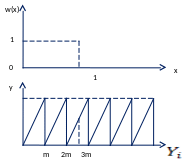
- большое → прямоугольник с координатами m, Y_{i max} является равномерно заполненным при различном значении i и m.

Реально используются более простые датчики:

1. Мультиплексивный датчик (Лемера)

2. Смешанный датчик

3. Аддитивный датчик

Формирование случайных чисел с законом распределения, отличным от равномерного

М ожно сформировать случайные числа, используя нелинейные операции.

Есть 2 числа U₁ и U₂, связанныем функциональной зависимостью U₂(U₁) :

На этом соотношении основан метод обратной функции. Требуется сформировать случайную величину и с плотностью вероятности из случайной величины X, равномерно распределенного в интервале (0,1).

Н айти функцию u(x)

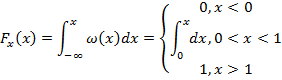
– обратная функция

Например для экспоненциального распределения

1 – e^-λu=x

e^-λu=1 – x

-λu=ln(1 - x)

u=-1/λ∙ ln(1 - x)

Методом обратной функции можно найти функциональную связь между случайными величинами только для ограниченного числа видов распределения.

Н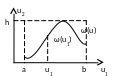 е требует каких-либо аналитических выражений для преобразования случайных величин метод отбора.

Позволяет получить случайную величину, если известен закон распределения.

Отбор производится пропорционально ее плотности вероятности по следующему алгоритму:

1. Генерируется пара равномернораспределенных случайных чисел

U₁ в интервале (a,b) и случайная величина U₂ в (0,h).

2. Проверяется, находится ли точка с координатами (U₁, U₂) ниже плотности распределения ω(u).

Решение: если (U₁, U₂) ниже ω(u), то принимается решение u= u₁, т.е. считается что значение u₁ ϵ u, если (U₁, U₂) выше ω(u), то испытания повторяются, а результат не учитывается.

Алгоритм генерирования:

1. Генерируется случайная величина x₁ равномернораспределенная в интервале (0,1).

2. Рассчитывается случайная величина U₁ равномернораспределенная в интервале (a,b). u₁=a-x(a-b).

3. Определяется значение плотности вероятности ω(u₁).

4. Генерируется случайная величина x₂ равномернораспределенная в интервале (0,1).

5. Рассчитывается U₂=x₂∙h, равномернораспределенная в интервале (0,h).

6. Если u₂ < ω(u₁), то u=u₁, если u₂ > ω(u₁), то значение u₁ обрабатывается.

7. Генерируется следующая пара чисел u₁ и u₂ и т.д.

Генерирование нормально распределенной случайной величины

В соответствии с центральной предельной теоремой, сумма большого числа СВ с произвольным законом распределения имеет закон распределения близкий к нормальному закону, поэтому этот метод, как правило, используют для генерирования нормальной СВ.

П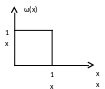 усть СВ равномернораспределены в интервале (0,1):

Одна СВ.

Какие значения принимает x₁+x₂:

П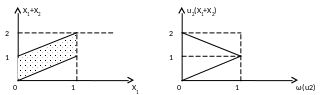 ри изменении количества слагаемых плотность вероятности будет изменяться так:

– сумма n-СВ

Найдем математическое ожидание и дисперсию:

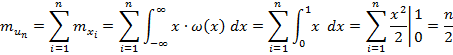
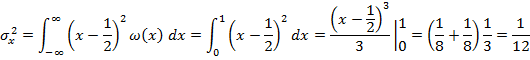
Обычно требуется генерировать нормированные СВ, имеющие нулевое мат ожидание и единичную дисперсию: