4. Использование критерия Лапласа при заданных вероятностях выбора природой своих стратегий

В случае известных вероятностях , , … , выбора природой своих стратегий , , … , соответственно по критерию Лапласа рассматривается ожидаемый выигрыш . Ожидаемый выигрыш игрока А для его стратегии определяется как математическое ожидание выигрыша игрока А при выборе им этой стратегий: = , = 1, 2, … , . Оптимальная стратегия игрока А определяется аналогично выбору оптимальной стратегии при неизвестных вероятностях стратегий природы. Стратегия игрока А будет оптимальной, при которой достигается максимум ожидаемого выигрыша : = . Если платёжная матрица определяет проигрыши игрока А и целью его будет достижение наименьшего проигрыша, то, как и в случае с неопределёнными вероятностями, оптимальной выбирается та стратегия , для которой = .

Пример 3. Задана платёжная матрица = , определяющая выигрыши игрока А в игре с природой. Заданы вероятности, с которыми природа выбирает свои стратегии: =0,1; =0,5; =0,3; =0,1. По критерию Лапласа определить оптимальную стратегию игрока А, при которой он получит максимальный выигрыш. Решить игру с природой, когда матрица С определяет проигрыши игрока А и его целью становится получение минимального проигрыша.

Решение. Для определения оптимальной стратегии платёжную матрицу представим таблицей, в которой в последнем столбце определим средние выигрыша игрока А по каждой из своих стратегий, а также максимальный выигрыш (табл. 3).

Таблица 3

Расчёт оптимальной стратегии выбора максимального выигрыша по критерию Лапласа с неопределёнными вероятностями выбора стратегий природой

	В1	В2	В3	В4	Средний выигрыш
А1	17	20	13	23	17,9
А2	22	14	19	12	16,1
А3	12	24	16	14	19,4
А4	21	10	20	11	14,2
А5	15	18	17	21	17,7
Вероятности выбора стратегий	0,1	0,5	0,3	0,1	19,4

Определяем средние выигрыши игрока по каждой стратегии: = = =17,9; = = =16,1; = = =19,4; = = =14,2; = = = 17,7.

Оптимальной стратегией будет стратегия А₃ с наибольшим ожидаемым выигрышем 19,4.

Ответ: = ; =18,25.

В случае минимизации проигрыша игрока А оптимальной будет стратегия А₄ с наименьшим ожидаемым проигрышем 14,2.

5. Выбор оптимальной стратегии по критерию Сэвиджа

Одним из показателей, по которому может выбираться оптимальная стратегия игрока А в игре с природой, может рассматриваться упущенная выгода игрока, если он выбирает стратегию, которая отличается от наиболее благоприятной стратегии при заданных условиях погоды. Этот показатель рассматривается как риск игрока А. Риск игрока всегда определяет его потери от выбранной стратегии, вне зависимости от того, что определяет платёжная матрица, выигрыши или проигрыши. По этому рассматривая риск как показатель, по которому выбирается оптимальная стратегия, игрок А стремиться всегда уменьшить свой риск. Целью его игры в этом случае будет минимизация риска.

По критерию Сэвиджа рассматривается в виде платёжной матрицы для принятия решений матрица рисков. Игрок А в качестве оптимальной стратегии выбирает максиминную стратегию, стратегию при которой достигается минимальный из гарантированных рисков.

Рассмотрим подробнее использование критерия Сэвиджа для принятия оптимальной стратегии.

Определим риски игрока А в случае максимизации выигрыша как разность наибольшего выигрыша его при выборе природой стратегии и выигрышем при данной стратегии : = . Для задачи минимизации проигрыша риск определяется как разность проигрыша при данной стратегии игрока и его минимальным проигрышем при выборе природы стратегии : = .

Строим матрицу рисков = 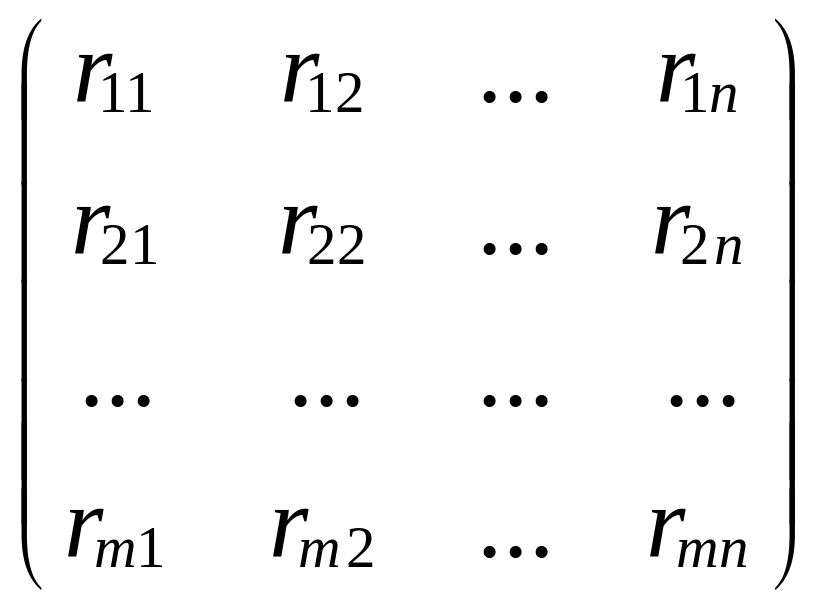. В этой матрице определяем гарантированные риски игрока А , в качестве которых берём наибольший из рисков, который может получить игрок А, выбрав данную стратегию: = . Смысл гарантированного риска состоит в том, что большего этого риска игрок А уже не получит, т. е. это наименьшее значение риска игрока А, который он получит, вне зависимости от выбора природы. В качестве оптимальной стратегии игрок А выбирает стратегию , при которой гарантированный риск наименьший: = .

Рассмотрим пример выбора оптимальной стратегии на основе критерия Сэвиджа, когда целью игры с природой является максимизация выигрыша игрока А.

Пример 4. Задана платёжная матрица = . По критерию Сэвиджа определить оптимальную стратегию игрока А, при которой он получит максимальный выигрыш.

Решение. Сначала построим матрицу рисков. Для этого в таблице выигрышей игрока А определим максимальные значения выигрышей для каждой стратегии природы (табл. 4).

Таблица 4

Расчёт максимальных выигрышей игрока А для стратегий природы

	В1	В2	В3	В4
А1	17	20	13	23
А2	22	14	19	12
А3	12	24	16	14
А4	21	10	20	11
А5	15	18	17	21
Максимальный выигрыш	22	24	20	23

Составим матрицу рисков, определяя её элементы по формуле: = .

= = . По матрице рисков определим гарантированные риски игрока А для каждой его стратегии по формуле: = (табл. 5). Также определим наименьший из гарантированных рисков.

Таблица 5

Расчёт оптимальной стратегии по минимальному гарантированному риску

	В1	В2	В3	В4	Гарантированный риск
А1	5	4	7	0	7
А2	0	10	1	11	11
А3	10	0	4	9	10
А4	1	14	0	12	14
А5	7	6	3	2	7
Минимальный гарантированный риск					7

Оптимальными стратегиями будут стратегии А₁ и А₅. Наименьший гарантированный риск 7. Ответ: = ; =7. Отметим, что для стратегии А₁ наибольший риск будет при стратегии природы В₃. Выигрыш игрока А для этой пары стратегий составит =13. Для стратегии А₅ наибольший риск получится при стратегии природы В₁. Для этой пары стратегий выигрыш составит =15. Поэтому предпочтительнее в такой ситуации игроку А выбирать стратегию А₅.

При поиске минимального проигрыша игрока А оптимальной будет стратегия А₄ с наименьшим ожидаемым проигрышем 14,2.

Пример 5. Задана платёжная матрица = . По критерию Сэвиджа определить оптимальную стратегию игрока А, при которой он получит минимальный проигрыш.

Решение. Для построения матрицы рисков в случае поиска минимального проигрыша в таблице проигрышей игрока А находим минимальные значения проигрышей для стратегии природы (табл. 8).

Таблица 8

Расчёт минимальных проигрышей игрока А для стратегий природы

	В1	В2	В3	В4
А1	17	20	13	23
А2	22	14	19	12
А3	12	24	16	14
А4	21	10	20	11
А5	15	18	17	21
Минимальный проигрыш	12	10	13	11

Теперь матрицу рисков определяем по формуле: = .

= = .

По матрице рисков определим также гарантированные риски игрока А и наименьший из гарантированных рисков (табл. 9).

Таблица 9

Расчёт оптимальной стратегии по минимальному гарантированному риску

	В1	В2	В3	В4	Гарантированный риск
А1	5	10	0	12	12
А2	10	4	6	1	10
А3	0	14	3	3	14
А4	9	0	7	0	9
А5	3	8	4	10	10
Минимальный гарантированный риск					9

Оптимальная стратегия А₄, наименьший гарантированный риск равен 9. Ответ: = ; =9.

Для стратегии А₄ наибольший риск будет при стратегии природы В₁. Проигрыш игрока А для этой пары стратегий составит =21.