Методическое пособие

Игры с природой

1. Особенности использования матричных игр в условиях неопределённости

Широкое применение теории матричных игр нашло в решении экономических задач, когда решения принимаются в условиях, имеющих случайную природу, а так же близких к случайному характеру условий или условиях, которые можно рассматривать как случайные. Если принимается условия, имеющие случайную природу, то полагается, что матричную игру можно повторять большое число раз в одних и тех же условиях, выбор стратегий можно осуществлять на основе условий статистической устойчивости условий матричной игры. В случае, когда условия матричной игры близкие к случайным, то предварительно нужно определиться с точностью и степенью доверия значений выигрышей и проигрышей игроков. Когда условия можно рассматривать как случайные, то нужно сформулировать границы, в которых предположение случайности будет приниматься. Неопределённость в игре может быть как полной, так и частичной, основанной на предварительной информации о возможных последствиях принимаемых решений и вероятности принятия стратегий некоторых игроков.

Также использование матричной игры в условиях неопределённости используется для игр, в которых число стратегий игроков большое. В этом случае тяжело использовать методы решения теории матричных игр при решении экономических задач из-за проблем связанных с большим количеством вычислений, а также с точностью полученных решений.

При неопределённости условий в теории матричных игр допускаются в игру игроки, которые принимают решения неосознанно, случайным образом. В таких играх полагается, что для игроков, играющих осознано, заданы выигрыши или проигрыши игроков, а для игроков, играющих неосознанно, выигрыши и проигрыши не рассматриваются.

Мы будем рассматривать только те игры природы, которые являются парными, в которых один игрок играет осознанно (игрок А), а второй игрок неосознанно (игрок В). Так как игрок В принимает решения неосознанно, случайным образом, то в качестве него рассматривается природа, а сама игра называется игрой с природой. В дальнейшем под игрой с природой мы будем понимать парную матричную игру, в которой игрок А выбирает свои стратегии осознано, а игрок В – случайным образом. И в такой игре игроком В будет природа. Для игрока А определяются выигрыши или проигрыши, которые задаются платёжной матрицей, а интерес природы не рассматривается. Выигрыш или проигрыш определяют значения наперёд заданного показателя эффективности для игрока А.

Чтобы подробно рассмотреть применение критериев выбора оптимальных стратегий, положим, что в игре с природой платёжной матрицей будет матрица = .

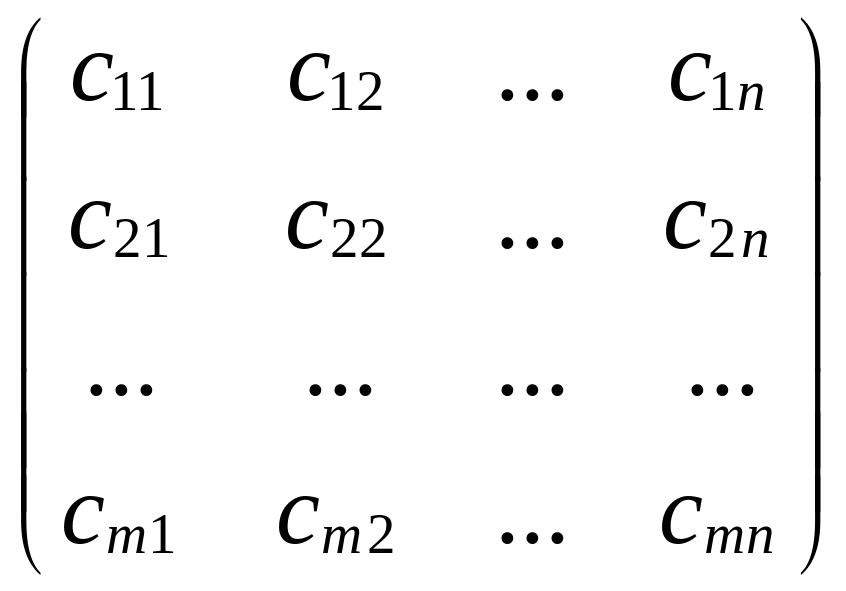2. Выбор оптимальной стратегии по критерию Лапласа

В качестве одного из критериев выбора оптимальной стратегии может рассматриваться среднее значение выигрыша для стратегий игрока А. Этот критерий называется критерием Лапласа. Использование критерия Лапласа может рассматриваться в случае, когда неизвестны вероятности выбора природой своих стратегий, и в случаях, когда такие вероятности известны. В первом случае предполагается, что природа выбирает свои стратегии с одинаковыми вероятностями. В качестве критерия тогда используется среднее арифметическое значение выигрыша для стратегии. Во втором случае показателем для использования критерия рассматривается математическое ожидание выигрыша для стратегий игрока А.

Критерий Лапласа используется для оценки выигрыша игрока в условиях неопределённости условий, при которых принимаются решения.

Рассмотрим каждый из возможных случаев использования критерия Лапласа в играх с природой отдельно.