Реакция струи

Реакцией струи называется сила, возникающая при истечении жидкости из насадка. Эта сила обусловлена изменением количества движения жидкости в насадке при движении от большого сечения к меньшему.

Пусть количество движения секундной массы жидкости в большем сечении насадка , а в меньшем .

Для определения величины и направления силы F воспользуемся законом изменения количества движения, согласно которому:

Учитывая, что < , и членом можно пренебречь, получим:

Учитывая, что m=ρQ, а , где - площадь выходного сечения насадка, получим:

Умножая числитель и знаменатель дроби на 2 и делая подстановки и γН=р, получим формулу для определения реакции струи в окончательном виде:

Знак минус указывает, что сила реакции направлена в сторону, противоположную движению струи.

Сила реакции струи для ручных стволов при напоре до 50 м достигает 500 Н; для лафетных стволов, работающих и при больших напорах, сила реакции увеличивается в несколько раз.

Пенные струи.

Кроме водяных струй при тушении пожаров используют и пенные струи.

Для пенных струй наблюдаются те же изменения формы, что и для водяных струй. При относительно небольших начальных скоростях струя сохраняет компактность по всей своей длине. С возрастанием скорости на струе образуются волны, но она еще некоторое время представляет сплошной поток, затем струя раздробляется на отдельные участки длиной по нескольку десятков сантиметров, постепенно их размеры уменьшаются, и уже летят отдельные хлопья пены.

Коэффициент сопротивления трению в воздухе можно определить по эмпирической формуле:

Распыленные струи и способы их получения.

Распыленная водяная струя представляет собой массу отдельно летящих капель. Для ее получения применяются специальные насадки, которые называют распылителями (диффузорные или конически расходящиеся).

Распыленная водяная струя характеризуется размером капель, их распределением по сечению струи, углом конусности струи, дальнобойностью, величиной напора перед насадком и расходом.

Капли жидкости при движении находятся под действием сил сопротивления воздуха, сил тяжести и капиллярных сил. Последние вследствие кривизны поверхности создают внутри капель избыточное давление, величину которого можно определить по формуле Лапласа:

где σ – коэффициент поверхностного натяжения воды; r – радиус капли.

При падении капли под действием силы тяжести с некоторой скоростью V в разных точках ее поверхности создаются различные давления. Вследствие разности давлений внутри капли возникает движение жидкости, капля меняет свою форму и разрушается на более мелкие части. Разрушение происходит до тех пор, пока не установится равновесие между капиллярными силами и динамическим действием воздуха на поверхность капли.

Диаметр капель и другие параметры, характеризующие струю, зависят, в основном, от способа получения распыленных струй. Практически наибольшее распространение нашли три способа получения распыленных струй: центробежный, пневматический и механический.

При центробежном способе поток жидкости поступает в камеру распылителя тангенциально и, вращаясь, перемещается на торцевой стенке форсунки.

При истечении жидкости из отверстия частицы жидкости разлетаются по прямолинейным линиям, касательным к цилиндрическим поверхностям, соосным с выходным соплом форсунки.

Теория движения идеальной жидкости в центробежном распылителе была разработана Г. Н. Абрамовичем, согласно которой тангенциальная составляющая скорости жидкости при выходе из отверстия равна:

Расход жидкости из форсунки определяется по формуле:

где µ - коэффициент расхода.

Практически чаще всего используются центробежные распылители с коэффициентом расхода µ = 0,24 – 0,65.

Конструкция форсунки, ее размеры и давления перед форсункой оказывают большое влияние на величину капель, форму факела и плотность распределения капель по сечению струи.

Средний размер капель можно определить по приближенной формуле И. Н. Новикова:

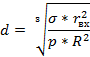
где p – давление жидкости перед форсункой.

В пожарном деле такие распылители применяются в ручных стволах и генераторах высокократной пены, в спринклерных и дренчерных системах.

При пневматическом способе распыление струи достигается подачей воздуха или пара в выходные сечения водяной струи. Воздух или пар подается либо под давлением, либо подсасывается (эжектируется), используя энергию самой струи. В пожарном деле такие распылители используются, в основном, для получения пенных и газоводяных струй.

При механическом способе дробление струи происходит вследствие удара ее о преграду. Из-за своей простоты этот способ нашел особенно широкое применение в пожарном деле. В качестве распылителя используют винтовой распылитель ударного действия, который представляет собой полый винт с переменным шагом и изменяющимся наклоном плоскостей. Каждый виток спирали срезает с водяной струи пленку, которая, ударяясь и срываясь с плоскости, разрывается на отдельные капли. При напоре 60 – 80 м распылитель обеспечивает получение капель размером 100 - 200 мкм.

Для получения распыленных струй применяют шаровые и щелевые распылители. Широкое применение находят также комбинированные распылители, в которых сочетаются сразу несколько способов распыливания воды.

Тема 9.2. Установившееся истечение жидкости из малого отверстия в «тонкой» стенке. Коэффициенты сжатия, скорости, расхода малого отверстия. Виды насадков. Истечение жидкости из внешнего цилиндрического насадка. Назначение насадков. Коэффициенты скорости и расхода насадков. Истечение жидкости из конических насадков. Истечение жидкости из отверстий и насадков при переменном напоре (2 час.).

Истечение жидкости из какого-либо резервуара может про­исходить через отверстия и насадки различных размеров и форм, короткие трубы как при постоянном, так и переменном напорах.

Струя из отверстия может истекать в атмосферу или под уро­вень жидкости, когда вытекающая струя будет распространяться в каком-то другом резервуаре или сосуде, в которых находится жидкость.

При истечении в атмосферу отверстие будет незатоплен- ным так же, как и струя, вытекающая из него. Когда истечение происходит под уровень жидкости, отверстие является затоп­ленным.

Отверстие в резервуаре называется малым, если во всех I очках отверстия давление можно считать практически постоян­ным. Поэтому скорости в разных точках живого сечения струи иудут одинаковыми.

Обычно к малым отверстиям относятся такие, диаметр которых d <

Отверстием в тонкой стенке называется отверстие, если юлщина стенки резервуара δ не влияет на условия истечения сгруи. При истечении жидкости потери напора в этом случае практически аналогичны местным потерям в результате внезап­ного сужения потока. К отверстиям в тонкой стенке относят слу­чаи, когда δ < 0,5d.

Струя жидкости при истечении из отверстия на расстоянии l₀ от входа сжимается и на этом расстоянии возникает сжатое сече­ние с-с с площадью живого сечения ω_с. Как показали опыты, расстояние до сжатого сечения l₀ ~ 0,5d. Сжатие струи происходит в результате сил инерции, действующих на частицы жидкости, движущиеся к самому отверстию по искривленным траекториям. В сечении с—с можно считать, что течение практически параллельно-струйчатое, т. е. линии тока жидкости параллельны друг другу и в нем заканчивается сжатие струн. Эпюра скоростей в этом сечении весьма близка к прямоугольной форме. За сжатым сечением струя падает под действие силы тяжести.

Коэффициент сжатия струи ε определяется по формуле

На сжатие струи влияют границы стенок, которые могут на­ходиться достаточно близко к отверстию. Опытами установлено, когда расстояние от кромок отверстия а > (3,5÷4)d и b > (3,5÷4)d

то боковые стенки и дно резервуара не влияют на степень сжатия струи. Такое сжатие получило название совершенного сжатия.

При истечении воды из малых отверстий, как было установлено опытами, в случае совершенного сжатия ε = 0,6 ÷ 0,64 при Re > 25 000. Несовершенное сжатие происходит при несоблюдении условия совершенного сжатия и сжатие струи уменьшается, а коэффициент сжатия увеличивается по сравнению с совершен­ным сжатием.

Большие отверстия — отверстия, в которых давления в пре­делах живого сечения существенно различаются. В связи с этим скорости в разных точках различны.

Насадками называют короткие патрубки, присоединенные к стенке резервуара, когда их длина l = 3 ÷ 8d (d — диаметр отвер­стия).

Для определения скорости и расхода жидкости, вытекающей из отверстия, используем уравнение Бернулли. Принимаем сече­ние 1-1 по свободной поверхности жидкости в резервуаре, второе сечение 2-2 проведем через сжатое сечение струи с-с. Плоскость сравнения 0-0 проводим через центр сжатого сечения параллель­но свободной поверхности (см. рис. 6.1). Истечение жидкости осуществляется в атмосферу.

Напишем уравнении Бернулли для сечений 1 – 1 и 2 – 2

где Р_оаб - абсолютное давление на свободной поверхности жидкости в резервуаре; V₁ V_c — средние скорости в соответствующих сечени­ях; z_c = 0; h_r — потери напора на участке от сечений 1—1 и 2—2.

Согласно формуле Вейсбаха

где ζ – коэффициент местных сопротивлений отверстия

Принимаем (P₀ – избыточное давление в сечении 1 – 1).

Следовательно,

Скорость V₁ – в резервуаре можно пренебречь, считая что площадь его поперечного сечения Ω многократно больше сечения отверстия, Ω >> ω_c. назовем приведенным напором.

Тогда

Откуда скорость в сжатом сечении

Введем следующее обозначение

где φ называется коэффициентом скорости истечения.

Окончательно формула скорости истечения будет иметь сле­дующий вид:

Для частного случая, когда Р₀ = Р_а, т.е. резервуар сообщается с атмосферой

В результате скорость

Для идеальной жидкости потери напора h_r = 0 и ζ = 0, а ко­эффициент скорости φ = 1.

Теоретическая скорость истечения в этом случае

Теоретическая скорость истечения в этом случае

Формула Торричелли, полученная им в 1643 г. на основании опытов при определении скоростей истече­ния в случае разных напоров Н.

Физический смысл коэффициента φ заключается в том, что он выражает отношение действительной скорости V_c к теоретиче­ской.

Зная скорость истечения, можно найти расход Q. При усло­вии, что Р₀ = Р_а

Назовем произведение двух коэффициентов ε, φ коэффици­ентом расхода отверстия μ

Тогда выражение для расхода при истечении через отверстие

Коэффициент расхода учитывает как степень сжатия, так и потери напора h_r, характеризующиеся коэффициентом местных сопротивлений С,.

Коэффициент μ определяется опытным путем и его значение изменяется в диапазоне 0,59 ÷ 0,64. Как правило, для предвари­тельных расчетов принимается μ₀ = 0,62.

Следует отметить, что при истечении через малые отверстия непрямоугольного сечения происходит деформация поперечного сечения струи. Форма деформированного сечения отличается от формы сечения отверстия, из которого происходит истечение. Такое явление носит название инверсии струи, которая связана с поверхностным натяжением жидкости и инерцией. Например при истечении из круглого отверстия поперечное сечение имеет форму эллипса, а для квадратного сечения струя приобретает крестообразную форму.

Зависимость коэффициента истечения из малых отверстий в тонкой стенке от числа Рейнольдса

Формула расхода аналогична формуле расхода из затопленного отверстия незатопленного отверстия. Различие формул заключается в том, что напор истечения Н выражает разность уровней жидкости и резервуарах Н₁-Н₂.

Истечение из затопленного отверстия

Установлено при проведении многочисленных опытов, что значения μ, φ для затопленного и незатопленного отверстий практически одинаковы. Поэтому в случае определения расхода пни скорости через затопленное отверстие коэффициенты при­нимаются такими же, как и для незатопленного отверстия. На ос­новании опытов разных авторов А. Альтшулем был создан гра­фик коэффициентов φ, ε, μ в зависимости от числа Рейнольдса для малых круглых отверстий. Для квадратичной об­ласти сопротивления при турбулентном режиме, т. е. при боль­ших числах , принимаются в ε= 0,63÷0,64; ζ= 0,06; φ=0,97; μ=0,62.

При определении дальности вылета струи при истечении жидкости и нахождении коэффициента скорости требуется знать траекторию струи. Для расчета располагаем в сжатом сечении струи начало координатных осей x и z. Частица жидкости массой Δт в сечении с-с имеет скорость V_c

Путь, пройденный частицей при равномерном прямолиней­ном движении, за время t

На частицу жидкости действует сила тяжести при ее падении. Расстояние падения за t

Пренебрегаем сопротивлением воздуха при движении материальной частицы жидкости. Уравнение траектории движения получим, подставив в выражение через t

Зная высоту падения z0, можно найти дальность вылета струи

Для начальной скорости получим следующую зависимость:

Коэффициент скорости по

Подставляя скорость согласно выражению в формул φ, получаем

таким образом, зная координаты струи х, z, можно вычислить значение коэффициента скорости φ.

Истечение жидкости через насадки

Насадки делятся на три основных типа: цилиндрические, ко­нические и коноидальные.

Цилиндрические насадки могут быть внешними или внут­ренними

На входе в насадки имеются достаточно острые кромки. Внешняя насадка присоединяется к наружной стороне резервуара к отверстию того же диаметра под прямым углом. Длина патруб­ка составляет порядка l = (2÷6)d. В результате обтекания острых кромок на входе в насадку происходит сжатие струи внутри на­садки, так же при истечении из малого отверстия. За сжатым се­чением площадью ω следует расширение струи до поперечного сечения самой насадки. Непосредственно в зоне сжатого сечения возникает вихреобразование в виде кольцевой водоворотной области. Скорость струи в сжатом сечении существенно больше скорости на входе в насадку, в результате этого в этой области давление становится меньше атмосферного, т. е. создается вакуумметрическое давление.

Максимальное вакуумметрическое давление Р_вак будет иметь место непосредственно в сжатом сечении. На границе водоворот- пой области ближе к выходу из насадки Р_вак = 0.

Запишем уравнение Бернулли относительно плоскости сравнения 0-0, проходящей по оси насадки. Сечение 1-1 при­нимаем по свободной поверхности жидкости в резервуаре, а сечение 3-3 на выходе из насадки. Давление на поверхности жидкости в резервуаре Р_а, а истечение жидкости осуществля­ется в атмосферу

Скоростью V₁ резервуаре пренебрегаем. Принимаем , .

Гидравлические потери на участке от 1 – 1 до 3 – 3 с учетом потерь по длине

В результате, после соответствующих подстановок, получим

где - суммарный коэффициент сопротивления на участке от 1 – 1 до 3 – 3.

Потери напора, возникающие при движении жидкости через насадки, можно разделить как

где - потери напора от свободной поверхности (сечение 1-1) до сжатого сечения с-с (сечение 2-2)

h_rвр— потери напора между сечениями 2—2 (сжатое сечение) и полным живым сечением на выходе из насадки (сечение 3—3). Считаем их как потери напора при внезапном расширении

Коэффициент местных сопротивлений при внезапном расширении

где ε – коэффициент сжатия; ; h_l – потери напора по длине насадки

Тогда потери напора в насадке

Скорость потока жидкости на выходе из насадки согласно после преобразований

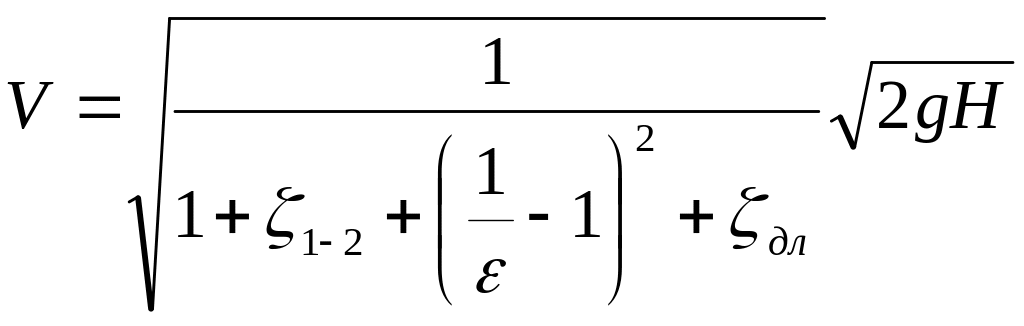
Обозначим коэффициент скорости насадки

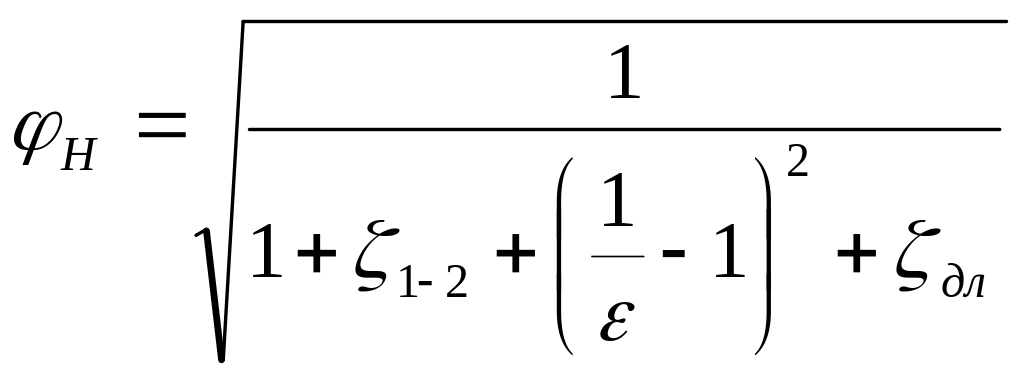
Формула скорости истечения из насадки окончательно представляется в известном ранее виде

Расход жидкости, проходящий через насадку

Так как насадка не имеет сжатия на выходе из него, то ε = 1, и для цилиндрической насадки коэффициент расхода насадки μ_н равен коэффициенту скорости φ_н

В результате проведения опытов установлено, что при длине насадки / = (2÷4)d можно не учитывать сопротивление по длине насадки, ζ_дл = 0.

При достаточно больших значениях числа Re сумма коэффи­циентов ζ_1-2 (коэффициент на сужение потока) и ζ_вр (расширение потока) в среднем, как показали численные подсчеты, равна

В результате скорость на выходе

Для цилиндрической насадки коэффициент скорости

В случае когда длина насадки l > 4d, следует учитывать потери напора по длине. Суммарный коэффициент сопротивлений

Коэффициент скорости

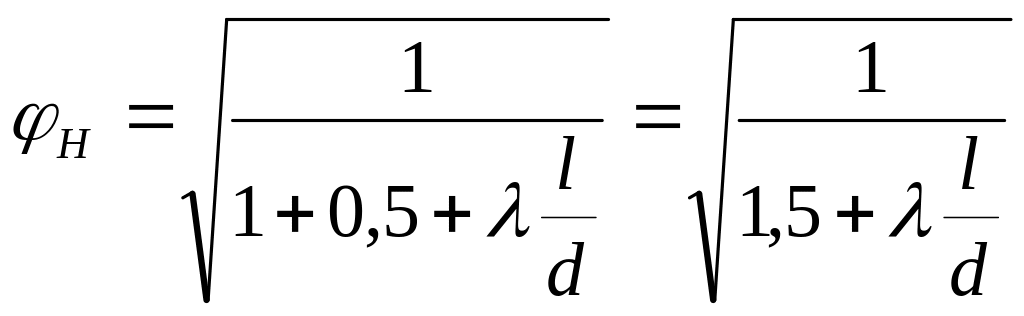
Так как φ_н = μ_н , то коэффициент расхода при l > 4d

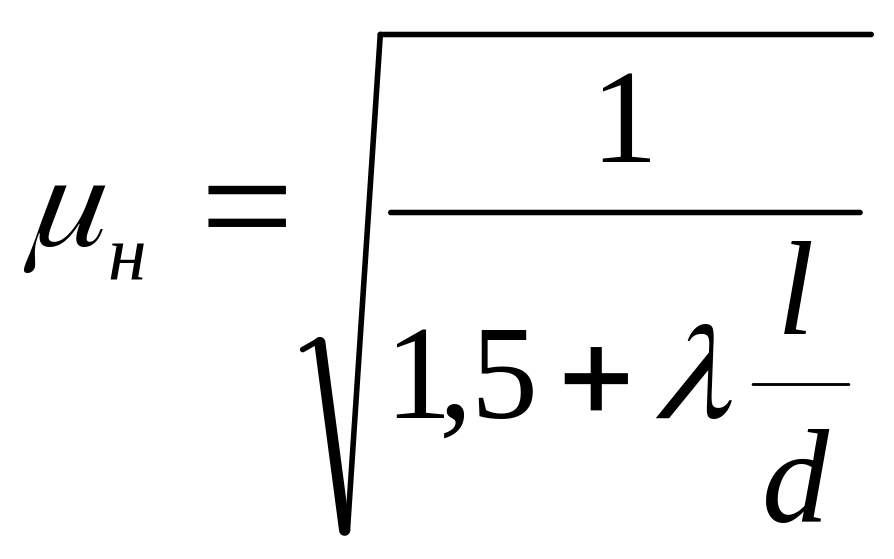
В результате увеличения скорости V_c в сжатом сечении воз­растает вакуумметрическое давление. При значительной разности атмосферного давления и вакуумметрического давления воздух может поступать в насадки через выходное сечение. В результате поток будет полностью отрываться от стенок насадки и будет происходить срыв вакуума. Насадка будет работать как при исте­чении из отверстия. Расход, проходящий через насадку, умень­шится и будет соответствовать расходу как из отверстия в тонкой стенке.

Для внешней цилиндрической на­садки коэффициент скорости φ_н ≈ 0,82. Коэффициент сжатия струи в насадке принимаем ε ≈ 0,64. Согласно вышеизложенному определим вакуумметрический напор с уче­том напора Н

Опытами было установлено, что срыв вакуума происходит, когда максимальный вакуумметрический напор м и на­чинается подсасывание воздуха через выходное отверстие насад­ки, а истечение жидкости осуществляется аналогично отверстию в тонкой стенке.

Предельное значение напора H, при котором истечение из насадки при l ≥ (3 ÷ 4)d без срыва вакуума, будет составлять

м.

Таким образом, истечение струи из внешней цилиндрической насадки полным сечением будет происходить при H_вак ≤ 8 м и предельным напором Н_пр ≤ 10,5 м при длине насадка l ≥ (3÷4)d.

Цилиндрическая насадка, находящаяся внутри резервуара, называется внутренней насадкой. На входе в такую насадку поток (струя) претерпевает большее сжатие, чем это име­ет место во внешней насадке. Причиной этого является обтекание потоком входного отверстия насадки с относительно малой тол­щиной по кромке δ. Сопротивления на входе, связанные с дефор­мацией потока, зависят от относительной толщины передней кромки насадки -

Установлено, если l ≤ 3d, то истечение происходит аналогич­но истечению из малого отверстия, т. е. струя, отрываясь от кро­мок, не касается стенок насадки. При Re > 10⁴ получены следую­щие значения коэффициентов. Коэффициент скорости φ_н = 0,98; коэффициент расхода μ_н= 0,5; коэффициент сжатия ε = 0,51. Зна­чения коэффициентов μ, ε значительно меньше, чем для отвер­стия в тонкой стенке.

В случае увеличения длины насадки l > 3d внутренняя насад­ка работает, как правило, полным сечением, при Re > 10⁴ имеем μ_н= φ_н= 0,71; ε = 1.

Конические насадки. К коническим насадкам относятся схо­дящиеся и расходящиеся насадки. Сходящаяся насадка имеет форму усеченного конуса, образующие которого направлены к выходному отверстию. В таких насадках деформация потока дос­таточно мала, водоворотная вихревая область незначительна и поте­ри напора существенно меньше, чем у цилиндрической насадки.

Опытами установлено, что коэффициент расхода для малых круглых отверстий конических насадок достигает максимальных значений μ_н = 0,94÷0,95 при угле конусности β= 12-14°, а коэф­фициент сжатия на выходе ε ≈ 0,99. Увеличение угла β > 14° при­водит к уменьшению μ_н и увеличению сжатия струи на выходе. Для квадратных и прямоугольных форм сечения насадок угол конусности принимается β ≈ 26°, при этом коэффициент расхода μ_н = 0,92÷0,93.

Применение сужающих насадок позволяет получить ком­пактную струю с достаточно большой скоростью истечения. На­садки такого типа применяются в различных струйных аппаратах, гидромониторах, пожарных наконечниках и т. д.

У расходящихся насадок происходит расширение сечения под углом конусности β. В такой насадке наблюдается достаточ­но большой отрыв потока от входных кромок, в результате водо­воротная область увеличивается и, следовательно, площадь сжа­того сечения уменьшается.

Вакуумметрический напор в сжатом сечении становится не­сколько больше, чем у внешней цилиндрической насадки с уве­личением угла конусности β.

Конические насадки

Угол конусности рекомендуется устанавливать β = 10÷12°.

Опытами установлено, что при угле β ≈ 8° и l = 9d значения μ_н = φ_н≈0,45.

Расход, проходящий в насадку, определяется по следующей формуле:

где ω₀ – площадь выходного отверстия

При сравнении внешней цилиндрической и расходящейся на­садок при одинаковых входных отверстиях расход последнего будет существенно большим.

Расходящиеся насадки используются в пожарной технике для распыления с помощью пенных огнетушителей, при увлажнении почв, в водоструйных насосах, гидроэлеваторах, в городских и пар­ковых фонтанах для создания струи разных видов и форм и т. п.

Коноидальная насадка представляет собой улучшенный тип сходящейся насадки, у которой форма входного отверстия имеет плавное очертание. Плавное входное отверстие не вызывает отрыва потока от стенок, устраняет прак­тически сжатие струи внутри насадки, в результате этого потери напора сводятся к минимуму. Значения коэффициен­тов и μ_н и φ_н зависят от формы скругления, шероховатости внут­ренней поверхности насадки. Обычно μ_н = φ_н принимаются в расчетах от 0,95÷0,98.

Насадки с плавным входом

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение

высшего профессионального образования

«Дальневосточный федеральный университет»

(ДВФУ)

ИНЖЕНЕРНАЯ ШКОЛА

МАТЕРИАЛЫ для ПРАКТИЧЕСКИХ ЗАНЯТИЙ

по дисциплине «Гидравлика»

Направление подготовки 20.05.01. «Пожарная безопасность»

Образовательная программа «Профилактика и тушение природных пожаров»

Форма подготовки: очная

г. Владивосток

2015

Практические занятия

(14 часов, в том числе 8 часов с использованием методов активного обучения)

Занятие 1. Физические свойства жидкостей и газов. (4 час.)

Задача 1.1. Определить плотность жидкости, полученной смешиванием 12 л бензина и 18 масла турбинного.

Задача 1.2. Определить избыточное давление на дне океана, глубина которого Н=10 км, приняв плотность морской воды ρ = 1030 кг/м³ и считая ее несжимаемой. Определить плотность воды на той же глубине с учетом сжимаемости и приняв модуль объемной упругости Е = 2 • 10³ МПа [3]

Задача 1.3. Определить плотность жидкости, если вес объема W = 15 л равен G = 160 Н.

Задача 1.4. Автоклав объемом W = 50 л наполнен водой и закрыт герметически. Коэффициент температурного расширения жидкости β_t, ее модуль упругости Е. Определить повышение давления в автоклаве при увеличении температуры жидкости на величину Т. Объемной деформацией автоклава пренебречь [6].

Задача 1.5. Канистра, заполненная бензином и не содержащая воздуха, нагрелась на солнце до температуры 50 °С. На сколько повысилось бы давление бензина внутри канистры, если бы она была абсолютно жесткой? Начальная и температура бензина 20 °С. Модуль объемной упругости бензина принять равным Е = 1300 МПа, коэффициент температурного расширения β_t = 8 • 10^-4 1/град [3].

Задача 1.6. В отопительной системе небольшого дома содержится объем воды W= 0,5 м³. Сколько воды дополнительно войдет в расширительный сосуд системы при ее нагревании от 20 до 90 °С [8]?

Задача 1.7. Определить изменение положения уровня жидкости в вертикальном цилиндрическом резервуаре, заполненным при 0 °С маслом и на высоту Н =2,7 м, при повышении температуры жидкости до 50 °С. Жидкость – масло индустриальное И-20. Деформацией стенок резервуара пренебречь.

Задача 1.8. Давление воды в заполненном толстостенном плотно закрытом сосуде равно 0,2 МПа. Как изменится давление при повышении температуры воды от 10 до 40 °С. Деформацией стенок сосуда пренебречь.

Задача 1.9. В отопительный котел поступает объем воды W = 45 м³ при температуре 60 °С. Какой объем воды W, будет выходить из котла при нагреве воды до температуры 90 °С?

Задача 1.10. Определить скорость υ равномерного скольжения прямоугольной пластины размерами (а b с) (а = 450 мм, b = 300 мм, c = 20 мм) по наклонной плоскости под углом α = 12°, если между пластиной и плоскостью находится слой масла турбинного толщиной δ = 1,2мм. Температура масла t = 45 °С, плотность материала пластины ρ_пл = 600 кг/м³ (рис. 1.1) [6].

Рис. 1.1. Схема к задаче 1.10

Задача 1.11. Определить силу трения Т и касательное напряжение τ, возникающее на внутренней поверхности трубы диаметром d = 25 мм и длиной l = 2 м при температуре воды t = 15 °С и разности скоростей между двумя соседними слоями толщиной мм, равной ди = 0,003 м/с.

Задача 1.12. Кольцевая щель между двумя цилиндрами (D =210 мм, d = 202 мм) залита трансформаторным маслом при температуре 20 °С (рис. 1.2). Внутренний цилиндр равномерно вращается с частотой п = 200 мин^-1. Определить динамическую и кинематическую вязкость масла, если момент, приложенный к внутреннему цилиндру, М = 0,065 Н • м, а высота столба жидкости в щели между цилиндрами h = 100 мм. Трением основания цилиндра о жидкость пренебречь. Определить мощность, теряемую на преодоление силы трения, возникающей на боковой поверхности цилиндра [3].

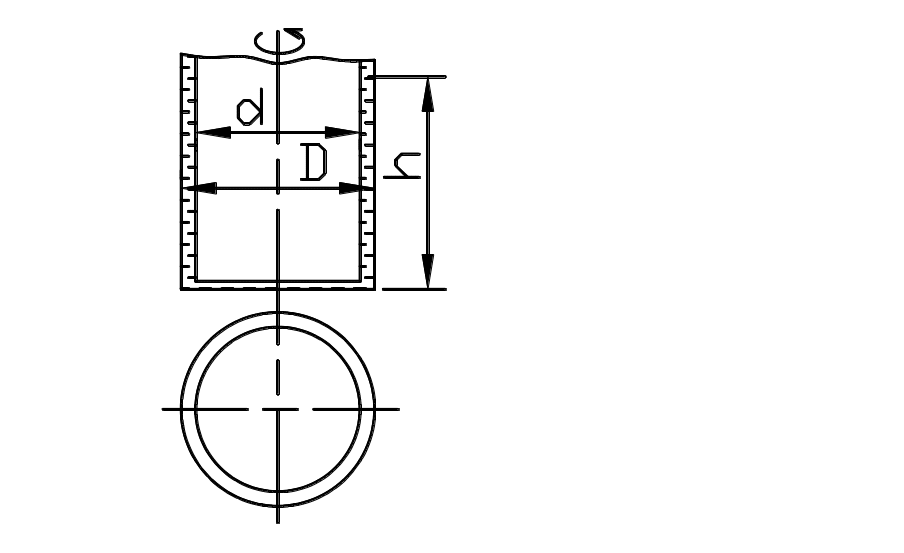
Занятие 2. Сила давления жидкости на плоские стенки и криволинейные поверхности. (4 час.)

Задача 2.1. Определить силу давления и построить эпюру давления воды на плоскую прямоугольную стенку шириной , наклоненную к горизонту под углом . Глубина потока слева в верхнем бьефе (верхнем участке водотока) Н = 8 м и справа от стенки (в нижнем бьефе) (рис. 3.5) [7].

Рис. 3.5. Схема к задаче 3.1

Задача 2.2. Определить силу давления воды и построить эпюру давления на плоскую треугольную стенку, наклоненную к горизонту под углом . Глубина потока слева и справа от стенки и ее ширина поверху показаны на рис. (рис. 3.6) [7].

Рис. 3.6. Схема к задаче 3.2

Задача 2.3. Горизонтальная металлическая цистерна круглого сечения диаметром D = 2 м и длиной полностью заполнена минеральным маслом. Давление на поверхности масла равно атмосферному. Следует определить силу давления масла на внутреннюю криволинейную поверхность цистерны (рис. 3.7) [11].

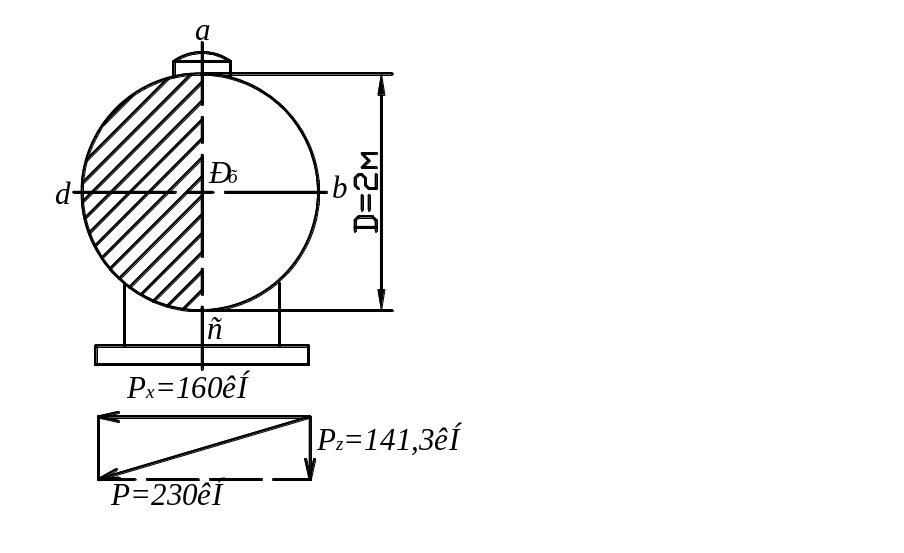
Рис. 3.7. Схема к задаче 3.3

Задача 2.4. Круглое отверстие в дне резервуара с водой (рис. 3.8) диаметром D = 40 см перекрывается клапаном-полусферой радиуса R = 20 см.

Рис. 3.8. Схема к задаче 3.4

Вычислить:

а) силу T, необходимую для поднятия клапана при напоре , если вес клапана , а давление на свободной поверхности равно атмосферному;

б) при каком значении Н клапан откроется автоматически, если [5].

Задача 2.5. Квадратное отверстие ( ) в вертикальной стенке резервуара с бензином ( = 750 кг/м³) закрыто крышкой (рис. 3.9). Найти силу давления на крышку и точку ее приложения, если центр отверстия находится на глубине H = 2,0 м, вакуум на поверхности жидкости р_вак = 60 кПа [13].

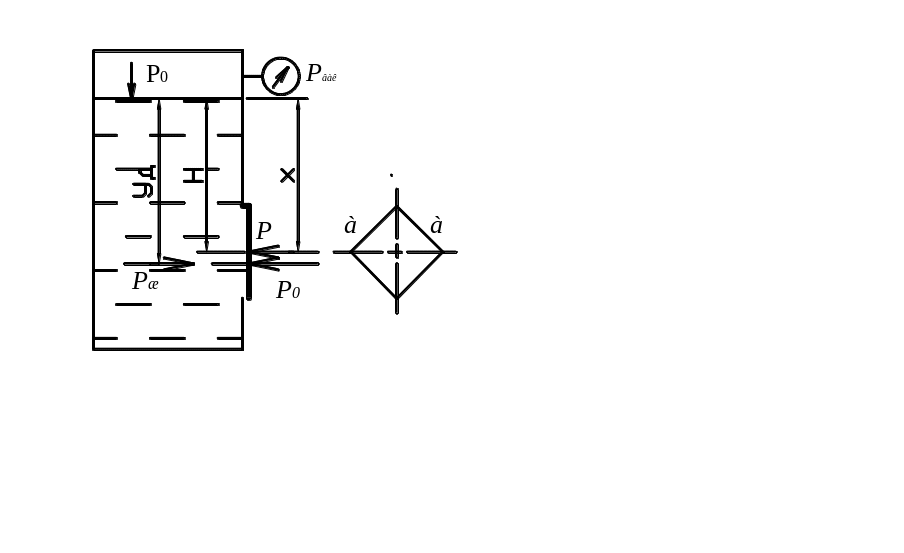
Рис. 3.9. Схема к задаче 3.5

Занятие 3.Уравнение неразрывности. Уравнение Д.Бернулли (4 час.)

Задача 3.1. В баке А вода подогревается до температуры 50 °С и самотеком по трубопроводу длиной l = 15 м попадает в производственный цех. Напор в баке А равен Н = 5 м. Каким должен быть диаметр трубопровода, чтобы обеспечивалась подача жидкости в количестве Q = 4 л/с при манометрическом давлении в конце трубопровода не ниже р_м = 70 кПа? Труба стальная сварная новая. Построить пьезометрическую и напорную линии (рис. 5.3) [27].

Рис. 5.3. Схема к задаче 5.1

Задача 3.2. Бензин сливается из цистерны по трубе диаметром d = 50 мм, на которой установлен кран с коэффициентом сопротивления Определить расход бензина при H₁=1,5 м и H₂=1,3 м, если в верхней части цистерны имеет место вакуум h_вак = 73,5 мм рт. ст. Потерями на трение в трубе пренебречь (рис 5.4) [26].

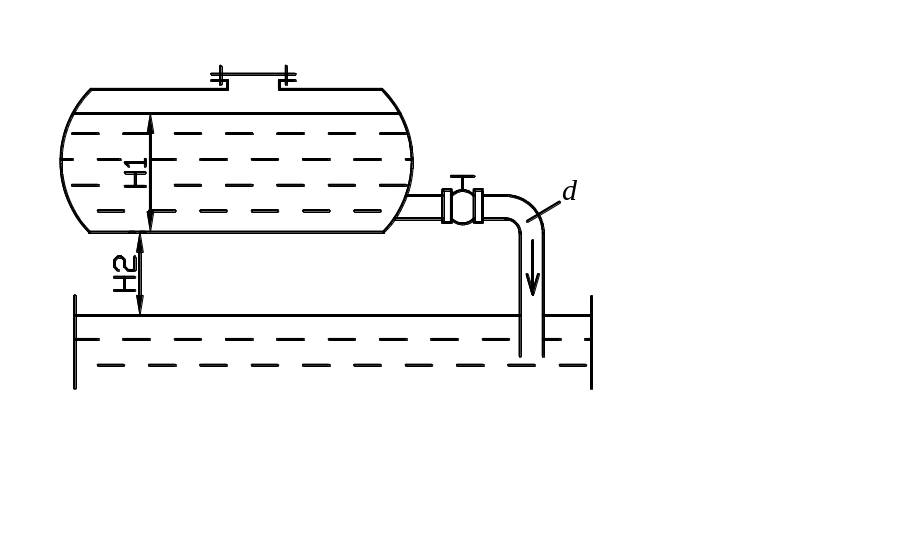
Рис. 5.4. Схема к задаче 5.2

Задача 3.3. Насос нагнетает жидкость в напорный бак, где установились постоянный уровень на высоте H = 2 м и постоянное давление ρ₂ = 0,2 МПа. Манометр, установленный на выходе из насоса на трубе диаметром d = 75 мм, показывает ρ₁ = 0,25 МПа. Определить расход жидкости Q, если диаметр искривленной трубы, подводящей жидкость к баку, равен d₂ = 50 мм; коэффициент сопротивления этой трубы принят равным = 0,5. Плотность жидкости = 800 кг/м³ (рис. 5.5) [26].

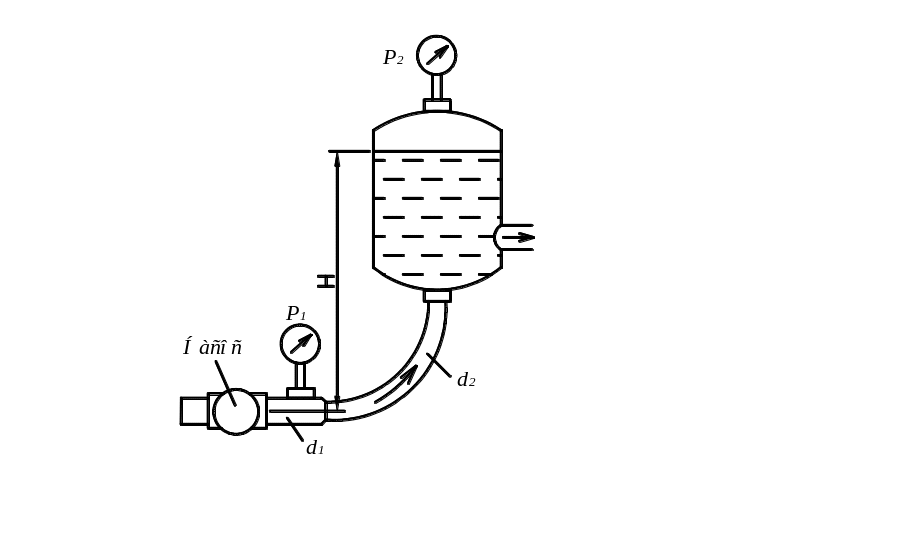
Рис. 5.5. Схема к задаче 5.3

Задача 3.4. Определить скорость на всех участках трубопровода переменного сечения, присоединенного к резервуару, расход, построить пьезометрическую и напорную линии. Решить задачу без учета сопротивлений.

Расстояние по вертикали от уровня воды в резервуаре до центра конечного сечения трубопровода H = 10 м, манометрическое давление на поверхности воды в резервуаре р_м = 0,6 ати, вода из трубопровода вытекает в атмосферу. Диаметры трубопровода равны: d₁ = 125 мм; d₂ = 63 mm; d₃ = 100 мм; d₄ = d₅ = 75 мм (рис. 5.6) [7].

Рис. 5.6. Схема к задаче 5.4

Задача 3.5. По горизонтальной трубе диаметром d₁ = 100 мм, имеющей сужение d₂ = 40 мм, движется вода (расход Q = 6 л/с). Определить абсолютное давление в узком сечении, если уровень воды в открытом пьезометре перед сужением h₁ = 1,5 м. При каком расходе воды Q ртуть в трубке, присоединенной к трубопроводу в узком сечении, поднимется на высоту h = 10 см, если при этом h₁ = 1,2 м? Потерями напора пренебречь (рис. 5.5) [13].

Рис. 5.7. Схема к задаче 5.5

Занятие 4. Режимы движения жидкости (4 час.)

Задача 4.1. Индустриальное масло ИС-30, температура которого 20 °С, поступает от насоса в гидроцилиндр по трубопроводу d = 22 мм. Определить режим течения масла, а также температуру, при которой ламинарный режим сменяется турбулентным, если подача насоса Q = 105 л/мин [13].

Задача 4.2. Определить режим движения глицерина в трубе диаметром d = 100 мм, если расход Q = 540 л/мин.

Задача 4.3. Применяемые в водоснабжении и канализации трубы имеют минимальный диаметр d₁ = 12 мм, максимальный диаметр d₂ = 3500 мм. Расчетные скорости движения воды в них составляют υ = 0,5...4 м/с. Определить минимальное и максимальное значения числа Рейнольдса и режим течения воды в этих трубопроводах [25].

Задача 4.4. Определить критическую скорость, отвечающую переходу от ламинарного режима к турбулентному в трубе диаметром d = 0,03 мм при движении воды, воздуха и глицерина при температуре 25 °С [25].

Задача 4.5. В трубке диаметром d = 0,05 м движется вода с расходом Q = 0,005 м³/с. Определить, изменится ли режим движения воды при возрастании ее температуры от 5 до 20 °С [29].

Занятие 5. Расчет потерь напора и давления на преодоление сил трения (4 час.)

Задача 5.1. Построить напорную и пьезометрическую линии для горизонтального трубопровода переменного сечения, присоединенного к резервуару. Вход потока из резервуара в трубопровод прямой, кромки трубопровода во входном сечении с острыми краями. Трубопровод новый, из стальных цельнотянутых труб (высота выступов шероховатости Δ = 0,05 мм). Диаметры и длины труб d₁ = 100 мм, l₁ = 150 м, d₂ = 50 мм, l₂ = 50 м. В конце трубопровода установлена задвижка, открытие которой частичное S/d = 4/8, со степенью расширения потока n 0,5. Расстояние по вертикали от уровня воды в резервуаре до оси трубопровода Н = 10 м. Давление на поверхности воды в резервуаре атмосферное, вода вытекает из трубопровода в атмосферу. Температура воды в трубопроводе t = 10 °C (рис. 5.1) [29].

Рис 5.1.

Задача 5.2. Центробежный насос (рис. 5.2), перекачивающий воду при температуре 20 ^оС, развивает подачу Q = 1,7 л/с. Определить допустимую высоту всасывания h_в, если длина всасывающего трубопровода l = 13,2, диаметр d = 50 мм, а показание вакуумметра не превышало бы p₁ = 68 кПа. Труба стальная бесшовная после нескольких лет эксплуатации. Построить пьезометрическую и напорную линии [27].

Рис. 5.2.

Занятие 6. Расчет потерь напора и давления на преодоление местных гидравлических сопротивлений(4 час.)

Задача 6.1. Из большого закрытого резервуара А (рис. 6.1.), в котором поддерживается постоянный уровень воды, а давление на поверхности воды равно р₁ = 32,6 кПа по трубопроводу, состоящему из двух последовательно соединенных труб, вода при температуре 20 °С течет в открытый резервуар Б. Разность уровней воды в резервуарах равна Н = 6,8 м. Длина труб l₁ = 9,3 м и l₂ = 8,3 м, диаметры d₁ = 50 мм и d₂ = 40 мм. Трубы стальные сварные умеренно заржавевшие. Определить расход Q жидкости, протекающей по трубопроводу. В расчетах принять, что местные потери напора составляют 20 % от потерь по длине [27].

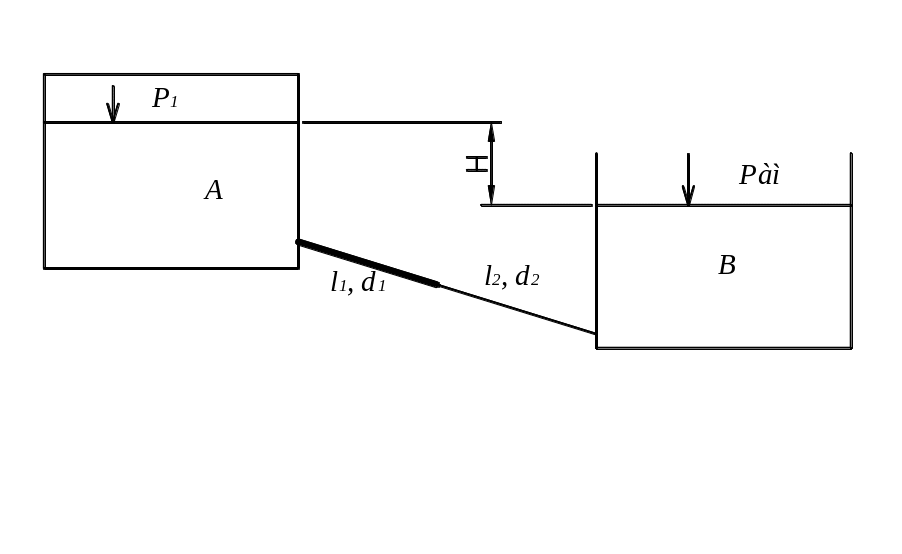
Рис. 6.1.

Задача 6.2. Определить коэффициент сопротивления вентиля, установленного в конце трубопровода диаметром d = 50 мм, если показание манометра перед вентилем р_ман = 3,7 кПа, а расход воды Q = 2,5 л/с [13].

Занятие 7. Гидравлический расчет простых трубопроводов.(4 час.)

Задача 7.1. По сифонному трубопроводу длиной l = 14 м вода при температуре 20 °С сбрасывается из отстойника А в отводящий канал Б. Какой должен быть диаметр d трубопровода, чтобы обеспечить сбрасывание жидкости в количестве Q = 2,6 л/с при напоре H = 4,8 м? Трубопровод снабжен приемным клапаном с сеткой (ξ_к = 7), а плавные повороты имеют углы 45° и радиус закругления R=2r. Построить пьезометрическую и напорную линии. Труба стальная сварная новая (рис. 7.1) [27].

Рис. 7.1.

Задача 7.2. Центробежный насос транспортирует бензин из резервуара А в резервуар В. Уровень бензина в резервуаре А H - 20 м. Определить высоту всасывания насоса, высоту нагнетания и давление, измеряемое в выходном сечении насоса. Исходные данные: расход бензина Q = 6,13 10^-3 м³/с, диаметр трубопровода d=0,05 м; коэффициенты потери напора на местные сопротивления: входа ζ_вых = 0,5; крана ζ_кр = 0,17; задвижки ζ = 2; выхода ζ_вых =1; l₁ = 6,5 м; l₂ = 116 м (рис 7.1) [6].

Рис 7.2.

Занятие 8. Расчет величины повышения давления при гидравлическом ударе в трубах(4 час.)

Задача 8.1 Произвести проверку на прочность стальной трубы диаметром d = 200 мм, в котором возможен прямой гидравлический удар. Толщина стенок трубы δ = 4, допускаемое напряжение на растяжение [σ]= 140 МПа, скорость движениея воды υ₀ = 5 м/с, давление до удара ρ₀ = 0,25 МПа.

Задача 8.2 К гидрораспределителю, время срабатывания которого Τ_з = 0,03 с, подводится расход масла (ρ = 900 кг/м³, E_ж = 1,35 × 10³ МПа) Q = 1 л/с по латунному трубопроводу длинной l = 7,5 м и диаметром D = 16 мм. Перед гидрораспределителем установлен шариковый предохранительный клапан диаметром d = 12 мм, жесткость пружинный которого c₁ 50 Н/мм (см. задачу 8.1). Определить величину предварительного поджатия пружины x₀, при котором клапан срабатывает при гидравлическом ударе, если толщина стенки трубопровода δ = 1 мм, модуль упругости латуни Е = 1,13 × 10¹¹ Па, начальное давление ρ₀ = 0,5 МПа.

Занятие 9. Расчет отверстий и насадков при постоянном и переменном напоре (4 час)

Задача 9.1. Из резервуара А, приток воды в который Q = 0,5 л/с, через малое отверстие диаметром d₁ = 15 мм вода перетекает в резервуар В, а из него через отверстие диаметром d₂ = 20 мм в атмосферу. Определить: а) напор Н₂ и разность уровней в резервуарах; б) при каком диаметре d₂ напор Н₂ = 0,5Н₁ (рис. 8.3) [5]?

Рис. 8.3. Схема к задаче 8.1

Задача 9.2 . Определить диаметр d отверстия в стенке резервуара для пропуска расхода Q = 5,20 л/с, если центр отверстия расположен на глубине h = 185 см от поверхности воды в резервуаре и на расстоянии е = 20 см от дна. Кромки отверстия острые [5].

Задача 9.3. Квадратное отверстие в стенке резервуара примыкает одной стороной а = 3,6 см к дну. Определить, при какой глубине h воды в резервуаре расход через отверстие будет Q = 4,18 л/с (рис. 8.4) [11].

Рис 8.4. Схема к задаче 8.3

Задача 9.4. Через цилиндрический насадок, расположенный в стенке, расходуется вода в количестве Q = 5,6 л/с. Диаметр насадка d = 3,8 см, длина l = 15 см. Определить напор Н над центром насадка, скорость v_c и давление р_е в насадке (рис. 8.5) [11].

Рис. 8.5. Схема к задаче 8.4

Задача 9.5. В бак, разделенный перегородками на три отсека, подается вода в количестве Q = 2,2 л/с. Температура жидкости 20 °С. В первой перегородке бака имеется коноидальный насадок, диаметр которого равен d = 40 мм, а длина l = 3d; во второй перегородке бака – цилиндрический насадок с таким же диаметром d и длиной l = 3d. Жидкость из третьего отсека через отверстие диаметром d поступает наружу, в атмосферу. Определить H₁, H₂ и Н₃ уровней жидкости (рис. 9.5) [27].

Рис. 9.5.

Задача 9.6. По трубопроводу (l = 300м, d = 100 мм, трубы сварные умеренно заржавевшие, Σξ = 18) вода при t = 10⁰ C поддается к пожарному брандспойту (конической трубке с цилиндрическим наконечником – соплом) с расходом Q = 20 дм³/с ( рис 9.6.). Превышение обреза сопла над осью трубопровода h = 3 м.

Определить необходимый диаметр сопла d_c и избыточное давление в начальном, сечении трубопровода p_м исходя из условия, что струя воды должна достигать высоты H = 15 м. Сопративление воздуха снижает ее на 20 %.

Рис 9.6.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение

высшего профессионального образования

«Дальневосточный федеральный университет»

(ДВФУ)

ИНЖЕНЕРНАЯ ШКОЛА

МАТЕРИАЛЫ для ОРГАНИЗАЦИИ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ

по дисциплине «Гидравлика»

Направление подготовки 20.05.01. «Пожарная безопасность»

Образовательная программа «Профилактика и тушение природных пожаров»

Форма подготовки: очная

г. Владивосток

2015

Гидравлика (72 час)

Работа по темам: дисциплину законспектировать и защитить

1. Свойства гидростатического давления: сформулировать и доказать. 2 час)

2. Относительный покой жидкости во вращающемся сосуде: используя дифференциальные уравнения Эйлера, вывести уравнение свободной поверхности жидкости. (2 час)

3. Относительный покой жидкости в случае прямолинейного движения сосуда с ускорением: используя дифференциальные уравнения равновесия жидкости Эйлера, получить уравнение свободной поверхности жидкости и закон распределения давления по глубине. (2 час)

4. Методы исследования законов движения жидкости: метод Эйлера, метод Лагранжа, Комбинированный метод. (2 час)

5. Уравнение Д. Бернулли для потока идеальной жидкости: интегрируя уравнение Д. Бернулли для элементарной струйки идеальной жидкости по живому сечению потока, получить уравнение для целого потока. (3 час)

6. Истечение жидкости из затопленного отверстия: при постоянном напоре дать определение затопленного и незатопленного отверстия, используя уравнение Д. Бернулли для двух сечений потока реальной жидкости, вывести формулы для расчета скорости истечения жидкости из затопленного отверстия и расхода. (3 час)

7. Истечение жидкости из отверстия при переменном напоре: используя уравнение для определения расхода жидкости, вытекающей из малого отверстия при постоянном расходе, получить зависимость для определения времени истечения объема жидкости из резервуара через отверстия при переменном напоре и сравнить со временем истечения такого же объема жидкости при постоянном напоре. (2 час)

8. Сила воздействия струи на преграду: вывести расчетную зависимость для определения величины силы давления жидкости на вертикальную стенку. (3 час)

9. Составить классификацию неньютоновских жидкостей в виде структурной схемы, привести примеры неньютоновских жидкостей и дать им краткую характеристику. (2 час)

10. Решение задач, оформление и защита задач (24 час)

11. Подготовка к экзамену. (27 час)

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение

высшего профессионального образования

«Дальневосточный федеральный университет»

(ДВФУ)

ИНЖЕНЕРНАЯ ШКОЛА

ГЛОССАРИЙ

по дисциплине «Гидравлика»

Направление подготовки 20.05.01. «Пожарная безопасность»

Образовательная программа «Профилактика и тушение природных пожаров»

Форма подготовки: очная

г. Владивосток

2015

ГЛОССАРИЙ

Вакуум {p_вак} – 1) состояние жидкости (или газообразной среды когда абсолютное гидромеханическое давление pА в ней меньше атмосферного pA<pа; 2) недостаток абсолютного давления (гидромеханического) до атмосферного (в той или другой точке или области жидкости)

p_вак=p_a-p_A.

Высота шероховатости стенок русла {Δ} – отдельные выступы на стенках русла, высота которых весьма мала по сравнению с поперечными размерами потока.

Высота пьезометрическая, отвечающая избыточному

(манометрическому) давлению в точке (избыточная пьезометрическая высота) {p_изб} – высота столба жидкости (заданного удаленного веса при атмосферном давлении на его свободную поверхность, создающего у своей подошвы давление, равное избыточному гидромеханическому давлению p_изб в рассматриваемой точке.

Вязкость жидкости – свойство жидкости, заключающееся в том, что при ее движении по поверхностям скольжения отдельных слоев ( или частиц) жидкости друг по другу возникают силы трения твой или другой величины (действующие вдоль поверхностей скольжения).

Гидродинамика – раздел механики жидкости (гидромеханики), в котором изучается движение жидкости, обусловленное действием приложенных к ней внешних сил.

Гидравлические сопротивления – силы трения, появляющиеся в жидкости при ее движении и вызывающие потери напора.

Гидравлический радиус {R} – параметр живого сечения потока, приближенно учитывающий влияние формы, а так же размеров этого сечения на среднюю скорость υ; величина этого параметра равна отношению площади живого сечения ω к длине смоченного периметра χ.

.

Гидравлический удар (явление гидравлического удара) – повышение или понижение гидромеханического давления в напорном трубопроводе вызванное изменением во времени в каком-либо сечении трубопровода скорости движения жидкости (например, путем открытия или закрытия задвижки).

Гидравлический уклон {ј_е} – 1) падение полного напора, приходящееся на единицу длины, отмеренную вдоль линии тока или вдоль потока.

Гидростатический закон распределения давления в жидкости – закон в соответствии, с которым гидромеханическое давление p для рассматриваемой области жидкости или рассматриваемой поверхности, намеченной внутри жидкости (например, для живого сечения потока), удовлетворяет условию

(для всех точек области или поверхности),

где z- отметка любой точки, принадлежащей рассматриваемой области (или поверхности); γ/p – пьезометрическая высота для этой же точки.

Гладкие русла (трубы) – русла, стенки которых имеют столь малые выступы шероховатости, что они не влияют при определенных числах Re на величину потерь напора по длине (при турбулентном движении).

Движение установившееся или стационарное – движение (течение) жидкости, при котором каждая неподвижная точка пространства, занятого движущейся жидкостью, характеризуется определенной скоростью течения, неизменной во времени по величине и по направлению.

Динамический коэффициент вязкости {μ} – 1) отношение продольного касательного напряжения внутреннего трения при прямолинейном движении жидкости к градиенту скорости по нормали .

Давление (в точке) гидростатическое {p} – величина этого давления равна пределу отношения элементарной силы гидростатического давления δP к величине, соответствующей элементарной площадке действия δS, при стремлении δS к нулю (при стягивании контура элементарной площадки в точку).

Давление (в точке) весовое гидростатическое {p_в} – гидростатическое давление, обусловленное только заглублением h рассматриваемой точки под свободной поверхностью жидкости и равное

,

где γ – объемный вес жидкости.

Давление (в точке) избыточное или иначе манометрическое, или иначе сверхатмосферное (гидростатическое, гидродинамическое или гидромеханическое) {p_изб} – давление в точке (гидростатическое, или гидродинамическое, или гидромеханическое, уменьшенное на величину атмосферного давления p_a.

_,

где p_A – абсолютное давление в точке.

Движение безнапорное – движение (течение) жидкости ( в русле), при котором поток имеет свободную поверхность.

Движение напорное – движение (течение), при котором поток жидкости со всех боковых сторон окружен твердыми стенками (не имеет свободной поверхности).

Движение неустановившееся (или нестационарное) – движение (течение) жидкости, при котором в каждой неподвижной точке пространства, занятого движущейся жидкостью, скорость движения ее частиц изменяется с течением времени по величине и (или) по направлению.

Живое сечение – поверхность, проведенная нормально к линиям тока и находящаяся внутри потока.

Жидкость аномальная – физическое тело, отличающееся от жидкости только тем, что оно в состоянии покоя может воспринимать некоторые относительно небольшие касательные напряжения.

Жидкость Бингама – воображаемая модель аномальной жидкости , отличающаяся от ньютоновской жидкости тем, что при градиенте скорости по нормали , равно нулю, величина продольных касательных напряжений внутреннего трения τ для жидкости Бингама (при прямолинейном ее движении) не равна нулю. В связи с этим величина τ для жидкости Бингама выражается зависимостью

,

где μ – динамический коэффициент вязкости.

Жидкость идеальная – воображаемая модель реальной жидкости, представляющая собой непрерывное жидкое тело, которое характеризуется абсолютной неизменяемостью объема (при изменении давления или температуры) и полным отсутствием вязкости.

Жидкость – физическое тело, обладающее: а) в отличие от твердого тела текучестью и б) в отличие от газа весьма малой изменяемостью своего объема (при изменении давления или температуры).

Жидкость неньютоновская – воображаемая модель жидкости, представляющая собой непрерывное тело, для которого продольные касательные напряжения внутреннего трения при прямолинейном движении жидкости прямо пропорциональны градиенту скорости по нормали в степени m, отличной от единицы:

,

где μ – динамический коэффициент вязкости.

Жидкость ньютоновская – воображаемая модель жидкости, представляющая собой непрерывное жидкое тело, для которого продольные касательные напряжения внутреннего трения τ при прямолинейном движении жидкости прямо пропорциональны первой степени градиента скорости по нормали :

,

где μ - динамический коэффициент вязкости.

Кинематика жидкости – часть раздела, называемого динамикой жидкости (гидродинамикой), в которой изучается движение жидкости без рассмотрения сил, определяющих это движение.

Кинематический коэффициент вязкости {v} – отношение динамического коэффициента вязкости к плотности жидкости ϱ

Конфузор – напорная труба, сужающаяся по течению.

Коэффициент гидравлического трения или коэффициент Дарси {λ} – безразмерный коэффициент пропорциональности в формуле Вейсбаха – Дарси, зависящий в самом общем случае только от относительной шероховатости стенок русла и от числа Рейнольдса.

Корректив кинетической энергии или коэффициент Кориолиса {α} – безразмерная величина, равная отношению кинетической энергии массы жидкости, протекающей за некоторый отрезок времени через данное плоское живое сечение, к условной кинетической энергии той же массы жидкости, подсчитанной в предложении, что во всех точках рассматриваемого живого сечения величины скорости одинаковы и равны средней скорости υ; величина

.

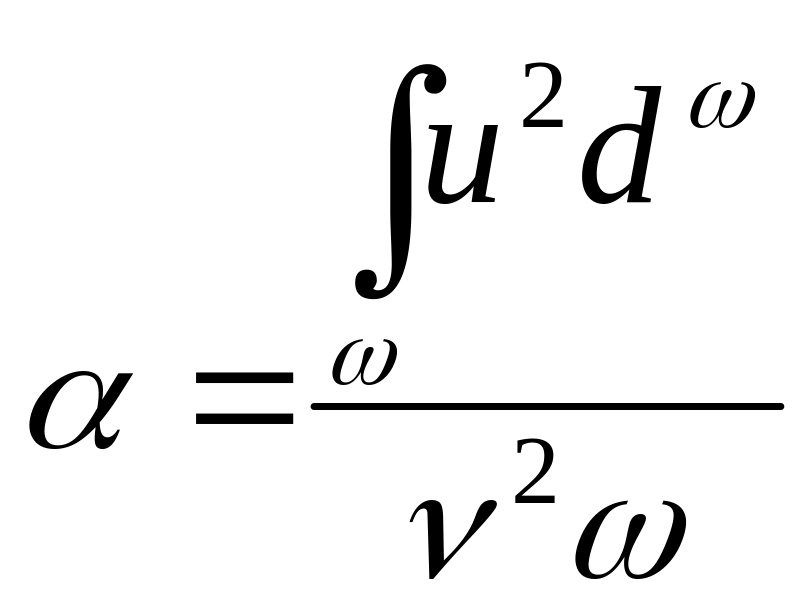Коэффициент расхода отверстия или насадка {μ} – безразмерный коэффициент, входящий в формулу для расхода, получающегося в случае истечения жидкости из отверстия в тонкой стенке или из насадка:

.

Кавитация – возникновение при снижении гидродинамического давления p пузырьков пара (или паровоздушных пузырьков) в толще движущейся жидкости (или у стенки русла) и захлопывание (в отличие от случая кипения этих пузырьков внутри жидкости (без выхода их из нее) в зоне, где гидродинамическое давление p повышается.

Ламинарный или вязкий подслой – слой ламинарно движущейся жидкости (весьма тонкий по сравнению с пограничным пристанным слоем), возникающий у стенок русла при турбулентном движении.

Ламинарный режим движения – движение (течение) жидкости, при котором ( в отличие от случая турбулентного движения частицы жидкости перемещаются по траекториям, направленным вдоль общего течения, без поперечного перемешивания, причем пульсации скорости и давления отсутствуют.

Местная потеря напора {h_м} – величина местного снижения полного напора потока, где он претерпевает местную резкую деформацию.

Насадок (или насадка) – весьма короткая напорная труба, при гидравлическом расчете которой можно пренебрегать потерями напора по длине.

Полный напор {H_e} – полная удельная энергия потока жидкости; полный напор равен сумме напоров потенциального и скоростного (кинетического).

Потеря напора по длине {h_l} – снижение полного напора на определенной длине потока, обусловленное работой сил трения.

Статика жидкости или гидростатика – раздел механики жидкости (гидромеханики), в котором изучается только равновесие жидкости (в частности, относительный ее покой).

Сила гидростатического давления (суммарное гидростатическое давление), действующая на поверхность твердого тела (или на поверхность, намеченную внутри жидкости) {P} – геометрическая сумма элементарных сил гидростатического давления, приложенных со стороны покоящейся жидкости ко всем элементарным площадкам, составляющим рассматриваемую поверхность.

Сила выталкивающая или архимедова {P_z} – направленная вертикально вверх сила гидростатического давления, действующая на поверхность неподвижного тела, погруженного в покоящуюся жидкость (полностью или частично).

Скоростной напор - удельная кинетическая энергия.

.

Силы массовые – внешние силы, действующие на все частицы жидкости, образующие рассматриваемый ее объем; величина их пропорциональна массе выделенного объема жидкости.

Техническая механика жидкости или техническая гидромеханика, или гидравлика – самостоятельная, сложившаяся техническая (прикладная) наука, представляющая собой механику жидкости, в которой широко используют различные допущения и упрощающие предложения, а так экспериментальные данные, причем, оперируя, как правило, теми или другими осредненными величинами, стремятся к оценке только главных характеристик явлений; в результате получают возможность решать при помощи относительно простых приближенных методов сравнительно сложные практические задачи механики жидкости.

Турбулентный режим движения - движение (течение) жидкости, при котором (в отличие от ламинарного движения) при котором частицы жидкости перемещаются по случайным неопределенно искривленным траекториям.