Тема 7.2. Основные особенности и закономерности ламинарного и турбулентного режимов движения жидкости. (2 час.).

Ламинарное движение является упорядоченным слоистым течением без перемешивания частиц жидкости в потоке. При ла­минарном движении векторы скорости частиц будут параллельны оси потока, поперечные скорости, перпендикулярные оси дви­жения, отсутствуют. Так как движение имеет слоистый характер, то между слоями, которые движутся относительно друг друга, будут возникать силы вязкостного трения и, следовательно, касательные напряжения. Движение жидкости подчиняется закону ввнутреннего трения Ньютона.

Скорость по оси потока при r = 0 — максимальная скорость u_max- найдем максимальную скорость

Расход

Средняя скорость V в поперечном сечении трубы

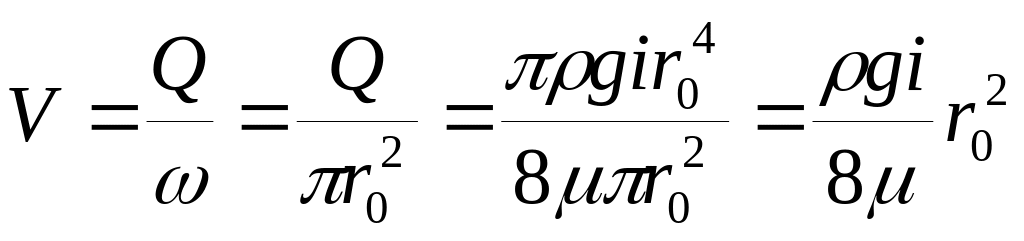
Сравниваем среднюю скорость V с максимальной скоростью в трубе u_max

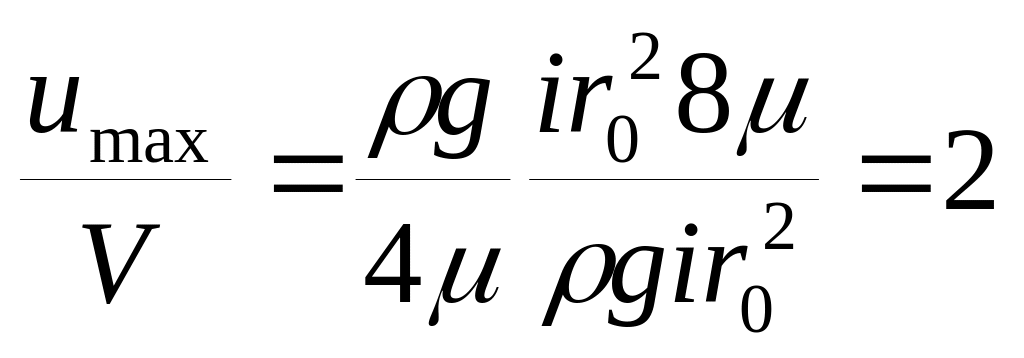
Средняя скорость в трубе при ламинарном движении в 2 раза меньше максимальной скорости

Потери напора по длине определим из формулы

или

Данная зависимость называется формулой Пуазейля - Гагена при определении потерь напора на трение по длине трубы для ламинарного режима движения.

где λ — коэффициент гидравлического трения для ламинарного режима движения жидкости.

Турбулентное движение жидкости наиболее часто встречает­ся как в трубах, так и в различных открытых руслах. В связи со сложностью турбулентного движения механизм турбулентности потока до настоящего времени все еще недостаточно полно изучен.

Турбулентному движению характерно неупорядоченное пе­ремещение частиц жидкости. Происходит движение частиц в продольном, вертикальном и поперечном направлениях, в результате этого наблюдается интенсивное перемешивание их в потоке. Частицы жидкости описывают весьма сложные траекто­рии движения. При соприкосновении турбулентного потока с шероховатой поверхностью русла частицы приходят во враща­тельное движение, т. е. возникают местные вихри различного размера.

Скорости в определенной точке турбулентного потока жид­кости можно измерить, например, с помощью лазерного прибора (ЛДИС). В результате измерений зафиксируется беспорядочная пульсация скоростей по направлениям х, у, z.

На рис. изображен график пульсации продольной мгно­венной скорости их с течением времени при условии установив­шегося движения потока жидкости. Продольные скорости их не­прерывно изменяются, колебания их происходят около некоторой постоянной скорости. Выделим на графике два достаточно боль­ших отрезка времени t₁ и t₂ и определим за время t₁ и t₂ среднюю по времени скорость их.

Осредненная (средняя по времени) скорость может быть най­дена как

График пульсации продольной мгновенной скорости и_х

Касательные напряжения, возникающие в турбулентном режиме, по своей физической природе существенно отличаются от касательных напряжений в ламинарном потоке. В результате интенсивного перемешивания частиц происходит массообмен частицами в поперечном направлении между отдельными слоями, что приводит к обмену количеством движения.

В турбулентном потоке имеют место вязкостные напряже­ния, связанные с силами внутреннего трения в результате сцеп­ления частиц в потоке, а также со стенками русла. Полные каса­тельные напряжения в результате турбулентного перемешивания τ_Т и вязкостного трения τ_В равны

Турбулентные касательные напряжения равны

В турбулентном потоке скорость движения частиц жидкости непосредственно у стенки трубы равна нулю. За счет вязкости жидкости на стенке трубы образуется тонкий заторможенный слой, который называется пограничным слоем, скорость на гра­нице которого составляет порядка 98 % скорости самого потока.Пограничный слой состоит из вязкого подслоя и переходного слоя, находящегося между турбулентным ядром и подслоем.

Внутри пограничного слоя может существовать как турбулентное, так и ламинарное движение в зависимости от числа Рей­нольдса

где u — скорость на внешней границе пограничного слоя.

В турбулентном ядре в результате интенсивного перемешивания и пульсации скоростей частиц жидкости распределение скоростей по живому сечению потока более ровное по сравнению с ламинарным режимом движения.

Как показали опыты, отношение средней скорости V и максимальной по центру трубы u_max находится в пределах = 0,75÷0,92.

В результате теоретических экспериментальных исследований по распределению скоростей в круглых трубах была предложена следующая зависимость для построении эпюры скоростей

где u - скорость в точке, располагающейся на расстоянии r от оси трубы; r₀ — радиус трубы; m — коэффициент, зависящий от числа Re_d.

Экспериментальные исследования показали, что шероховатость внутренней поверхности труб влияет на распреде­ление скоростей в живом сечении потока жидкости и на потери напора по длине.

Трубы изготовляются из различных материалов (сталь, чу­гун, бетон, стекло, полимеры и т. д.). Способ изготовления и вид материала влияют на шероховатость трубы. Шероховатость оп­ределяется высотой выступов и неровностей на поверхности сте­нок труб. С течением времени на внутренней поверхности труб появляется ржавчина, коррозия, отложение солей и осадков, что также будет влиять на шероховатость.

Характеристикой, выражающей шероховатость, служит средняя высота выступов и неровностей. Такая средняя высота, выраженная в единицах длины, называется абсолютной шерохо­ватостью и обозначается буквой к. Фактически шероховатость поверхности неоднородна по длине труб. На распределение ско­ростей и потери напора влияет также диаметр трубы при одина­ковой абсолютной шероховатости. Поэтому для определения влияния шероховатости и диаметра d введено понятие относительной шероховатости трубы - . Как показали опыты с трубами, на потери напора влияет не только средняя высота выступов к, но и форма, густота и характер их расположения. В связи с вышеперечисленными обстоятельствами было введено представ­ление об эквивалентной шероховатости к,. Эквивалентной ше­роховатостью называется высота выступов песчинок одинаково­го размера, при которой коэффициент гидравлического трения λ соответствует действительной естественной шероховатости трубы. Относительная эквивалентная шероховатость - .

На основании вышеизложенного следует, что при турбулент­ном движении потери напора по длине могут зависеть как от чис­ла Рейнольдса Re, так и от относительной эквивалентной шеро­ховатости -

Коэффициент гидравлического трения можно выразить функционалом

В зависимости от толщины вязкостного подслоя и погранич­ного слоя условно трубы можно разделить на гидравлически гладкие и шероховатые. В случае, когда вязкостный подслой δ_В больше шероховатости к, т. е. все впадины и выступы погружены в подслой δ_В > к, то такая поверхность стенки называется гидрав­лически гладкой.

Потери напора не будут зависеть от шероховатости и λ=f(Re).

При условии δ_В< к выступы выходят за пределы вязкостного подслоя и поверхности стенок являются шероховатыми.

При турбулентном движении коэффициент λ, определяется по эмпирическим формулам.

Шероховатость поверхности труб влияет на сопротивление движению, и такое сопротивление явля­ется квадратичным сопротивлением.

Для турбулентного режима движения было предложено большое число формул для нахождения λ. Предлагаемые фор­мулы были чисто эмпирическими, основывающимися на резуль­татах экспериментов, а также полученными в результате анали­за размерности и теории подобия при исследовании турбулент­ного режима. В формулах при определении коэффициента обычно использовалась эквивалентная шероховатость к_э. В таблице приведены значения к_э для труб, изготовленных из различных материалов.

Для всех областей турбулентного движения для определения λизвестны универсальные формулы Колбрука и А. Альтшуля.

Формула Колбрука

Формула Альтшуля

В области гладкого сопротивления (гидравлически гладкие трубы) δ_В > к_э и λ = f(Re), числа Рейнольдса лежат в следующих пределах:

Для гладких труб применяется формула Блазиуса

При определение λ гладких труб используется также формула П. Конакова

В области переходного сопротивления , числа Рейнольдса находятся в пределах

Формулы для определения коэффициента гидравлического трения

.

Тема 7.3. Местные гидравлические сопротивления. Виды местных сопротивлений. Теорема Борда. Экспериментальное определение коэффициентов местных сопротивлений. Взаимное влияние местных сопротивлений. Кавитация в местных сопротивлениях. (2 час.).

К местным гидравлическим сопротивлениям относят различ­ные устройства и элементы, устанавливаемые на трубопроводах, в которых происходит нарушение нормального движения потока в результате его деформации с изменением направления и вели­чины средней скорости и возникновением вихреобразования. В результате деформации турбулентного потока происходит интен­сивное перемешивание частиц и обмен количеством движения между частицами жидкости.

К элементам и устройствам относятся фасонная и трубопро­водная арматура: отводы (колена), переходники, тройники, кре­стовины, диафрагмы, сетки, запорные регулирующие вентили (краны), задвижки, затворы, предохранительные и регулирующие клапаны, всасывающие наконечники, устанавливаемые на входе в трубу насосов и т. д.

В результате обтекания преграды, находящейся в трубе, потоком жидкости происходит отрыв части потока от стенки трубы с возникновением вихревой зоны, которую называют водоворотной областью. Между водоворот­ной областью и основным потоком благодаря поперечным пульсационным скоростям происходит интенсивный обмен частицами жидкости.

Местными потерями напора называют затраты удельной механической энергии, обусловленные работой сил трения и вихреобразованием, в результате преодоления потоком жидкости местного сопротивления. На поддержание вихрей в определенной

Деформация турбулентного потока при обтекании преграды:

1 — труба; 2 — вертикальная преграда; 3 — водоворотная область; 4 — по­верхность раздела

Вейсбах предложил местные потери напора определять в зависимости от скоростного напора по формуле

где ζ — безразмерный коэффициент, называемый коэффициен­том местного сопротивления; V — средняя скорость в живом се­чении, как правило, непосредственно за местным сопротивлением.

Коэффициент ζ, показывает количество скоростных напоров, затрачиваемых на преодоление какого-либо местного сопротив­ления. В местном сопротивлении потери механической энергии при движении потока через него превращаются в тепловую энер­гию.

В случае внезапного расширения потока жидкости местные потери напора и коэффициент сопротивления можно определить теоретически.

Рассмотрим случай, когда трубопровод малого поперечного сечения диаметром d резко переходит в большое сечение диамет­ром d₂. Поток жидкости расходом Q движется по горизонтально­му трубопроводу, ось потока х и ось трубопровода совпадают. Выделим часть потока между сечениями 1 - 1 и 2 – 2.

Поток жидкости, выходящий из малого сечения, поступает в виде транзитной струи в большее сечение трубопровода. В месте внезапного расширения происходит отрыв потока от стенки. В месте отрыва возникает вихревая, водоворотная область, имею­щая кольцевую форму. Водоворотная область не участвует в поступательном движении потока. Между водоворотной обла­стью и струей возникает поверхность раздела. Поверхность раз­дела неустойчива, на ней происходит интенсивное перемешива­ние частиц в результате пульсации и возникновение вихрей.

В результате вихреобразования на границе поверхности раз­дела происходит интенсивный обмен частицами жидкости с тран­зитной струей. Струя на длине водоворотной области приобрета­ет вращательно-поступательное движение, т. е. появляется ок­ружная составляющая скорости. За водоворотной областью вращательное движение прекращается.

Полученная формула называется формулой Борда.

Введем в формулу Борда скорость V₁ через V₂ и вынесем за скобки V₂, получим

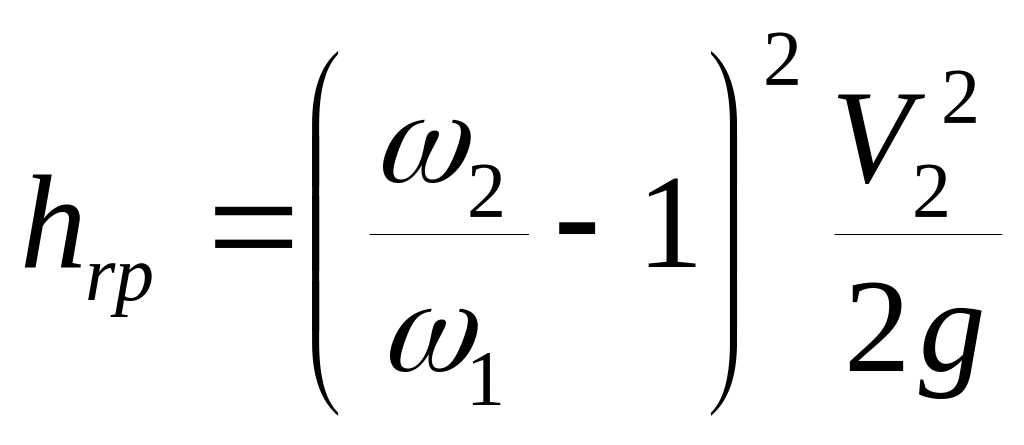
Обозначим

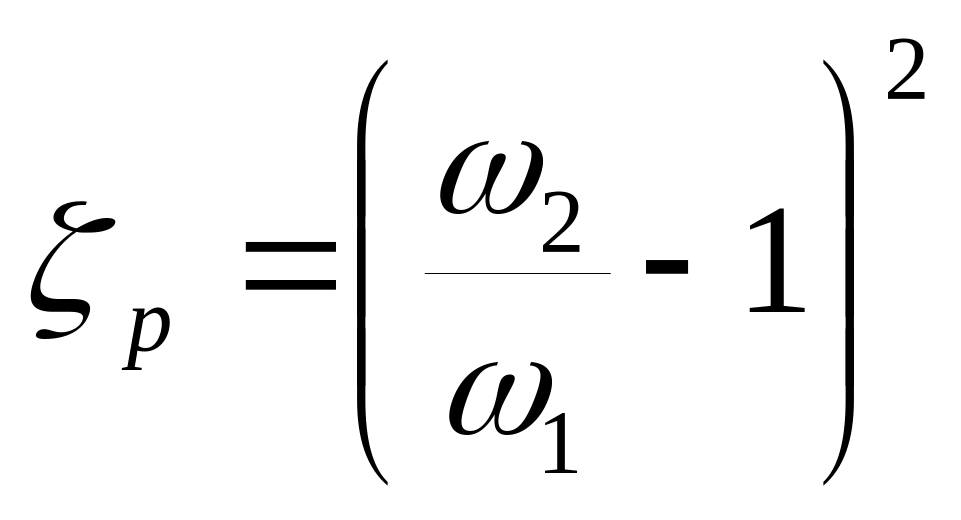
Тогда

где ζ - коэффициент местного сопротивления при внезапном расширении потока жидкости.