3.10. Прогнозирование по парной регрессионной модели

Под прогнозированием по парной регрессионной модели понимается нахождение неизвестных значений зависимой переменной для тех значений независимой переменной , которых нет в исходных наблюдениях. Различают точечное и интервальное прогнозирование. В первом случае оценка – некоторое число, во втором – интервал, в котором находится истинное значение зависимой переменной с заданной вероятностью.

Прогностические способности модели определяются величиной индекса детерминации. О достаточном качестве прогноза можно говорить, как правило, лишь при значении коэффициента (индекса) детерминации, большем 0,75.

Точечный прогноз результирующего признака y определяется путем подстановки в уравнение регрессии значения x_p независимого фактора: . В случае линейной модели .

Точечный прогноз явно не реален, поэтому он всегда дополняется расчетом доверительного интервала прогноза. В случае интервального прогноза по парной линейной модели предварительно рассчитывается стандартная ошибка прогноза:

, (3.5)

где .

Затем строится доверительный интервал прогноза

,

т.е. определяются нижняя и верхняя границы интервала прогноза.

Из формулы (3.5) следует, что ширина доверительного интервала прогноза зависит от стандартной ошибки регрессии (т.е. от качества модели), а также от значения x_p независимого фактора , как это видно на рисунке 3.7: при она минимальна, а по мере удаления от она увеличивается.

Отсюда следует, что интервальный прогноз реалистичен в пределах диапазона исходных данных. Экстраполяция кривой регрессии, т.е. ее использование вне пределов наблюдаемого диапазона значений объясняющей переменной, может привести к значительным погрешностям. Поэтому, в частности, долгосрочное прогнозирование по трендовым моделям, где в качестве независимой переменной выступает время, как правило, не оправдывает себя.

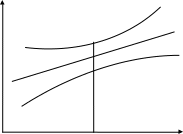
Рис. 3.7. Доверительная полоса линии регрессии

3.11. Обзор некоторых вопросов и проблем парной регрессии

Базовые понятия теории вероятностей и математической статистики в объеме, необходимом для анализа парных регрессионных моделей, представлены в [3-5].

Все оценки основных показателей парной регрессии приведены нами без доказательств. Строгие выводы их можно найти в [2-4].

Базовые нелинейные модели, используемые в парном эконометрическом моделировании, а также примеры их практического использования описываются в [3]. Здесь же охарактеризованы основные критерии «хорошей модели», которые следует учитывать при построении работоспособной модели и сравнении ее с другими моделями.

Считается, что при построении парной регрессионной модели число наблюдений должно в 7-8 раз превышать число рассчитываемых параметров при переменной x. Это означает, что искать линейную регрессию, имея менее 7 наблюдений, вообще не имеет смысла. Если же вид функции усложняется, то соответственно требуется увеличение числа наблюдений, ибо каждый параметр при x должен рассчитываться хотя бы по 7 наблюдениям. Если, например, мы выбираем параболическую модель , то требуется объем информации, предполагающий уже не менее 14 наблюдений.

Кроме оценки общего качества и статистической значимости, верификация парной линейной регрессионной модели предусматривает проверку модельных предположений (условий 1-5 классической нормальной линейной модели). Некоторые аспекты такой проверки рассматриваются в главе 5. Подробно проблемы тестирования и устранения негативных явлений в парных моделях (гетероскедастичности, автокорреляции и др.) излагаются в [2,3].

Мы рассматриваем оценку тесноты связи между переменными и как один из элементов верификации модели, хотя в ряде случаев ее полезно провести на этапе спецификации. Это связано с тем, что если линейный коэффициент корреляции оказывается недостаточно высоким (линейная связь слабая, умеренная или даже заметная), то уже на ранней стадии эконометрического моделирования следует задуматься о целесообразности выбора парной модели.

Вскрывая взаимосвязи изучаемых процессов, эконометрические модели не решают вопроса о причине этих взаимосвязей. Может оказаться, что совместные изменения переменных вовсе не означают наличия причинных связей между ними. И если это так, то одна из главных целей эконометрики, состоящая в выработке рекомендаций для принятия эффективного решения, не будет достигнута, так как будет неизвестно, на какой фактор надо воздействовать.

Именно потребность в причинном объяснении корреляции и привела американского генетика С.Райта к созданию метода путевого анализа. Путевой анализ основан на изучении всей структуры причинных связей между переменными и заключается в разложении коэффициента парной корреляции на четыре компоненты:

- компоненту прямого влияния (причина u, вызывающая y, задается действием переменной х);

- компоненту косвенного влияния (причина u воздействует на промежуточное звено х и тем самым вызывает у);

- непричинную компоненту, объясняемую наличием общих причин, воздействующих на х и на у;

- непричинную компоненту, зависящую от неанализируемой в модели корреляции.

Методика путевого анализа описана в [2].

О значимости коэффициентов линейной регрессии можно судить не только на основании критерия Стьюдента, но также и по значениям показателя Р-значение из таблицы «Дисперсионный анализ», рассчитанной в режиме работы инструмента "Регрессия" в MS Еxcel. Коэффициенты признаются значимыми, если Р-значение меньше заданного уровня значимости α=0,05. Это же касается и оценки значимости коэффициента детерминации.