
- •1.Предмет и его задачи.Класс-ция процессов.
- •3.Теоретические основы ПиАхт. Моделирование проц. И аппаратов.
- •4.Основные физ. Св-ва жидкостей и их смесей
- •5. Гидростатика. Ду равновесия ж-ти Эйлера.
- •6.Основное ур-е гидростатики.
- •8.Гидродинамика. Осн. Хар-ки движения жидкостей. Гидравлич-й радиус и эквивал-й диаметр.
- •9. Субстанцион-я производная.Режимы движения ж-тей. Опыты Рейнольдса.
- •10.Распред-е скоростей в цилиндрич-м канале при устан-мся ламин-м режиме.
- •11.Расход ж-ти при устан-ся ламинарном потоке в цилиндрич-м канале.
- •12.Основные хар-ки тулбулентного потока.
- •13. Вывод ур-я неразрывности потока.
- •14. Ду движения идеальной ж-ти Эйлера
- •15.Ду движения реальной ж-ти Новье-Стокса.
- •2. Общие принципы расчета хим. Аппаратуры.
5. Гидростатика. Ду равновесия ж-ти Эйлера.
В
гидростатике изучается равновесие
жидкостей, находящихся в состоянии
относительного покоя. При этом частицы
не перемещаются друг относительно друга
и относительно стенок емкости (сосуда),
в котором она находится. При этом силы
внутреннего трения отсутствуют
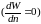 ,
а жидкость считается идеальной. Однако
в этом случае на частицу всегда действует
сила тяжести и давления, а в случае
перемещения емкости с жидкостью
необходимо учесть силу инерции переносного
движения жидкости.
,
а жидкость считается идеальной. Однако
в этом случае на частицу всегда действует
сила тяжести и давления, а в случае
перемещения емкости с жидкостью
необходимо учесть силу инерции переносного
движения жидкости.

Элементарная
сила тяжести направлена вниз параллельно
оси z.
Величина ее проекции на ось z
определяется как:
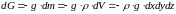 .Проекции
силы тяжести на оси x
и y
равны 0. Давление в жидкости является
функцией трех координат p=
f(x,
y,
z).
Сила гидростатического давления
действует на нижнюю грань параллелепипеда
по нормали, а ее проекция на ось z
равна
.Проекции
силы тяжести на оси x
и y
равны 0. Давление в жидкости является
функцией трех координат p=
f(x,
y,
z).
Сила гидростатического давления
действует на нижнюю грань параллелепипеда
по нормали, а ее проекция на ось z
равна
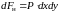 .Если
скорость изменения этого давления (т.е.
производная) в точке равна
.Если
скорость изменения этого давления (т.е.
производная) в точке равна
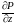 ,
то изменение давления по ребру dz
есть дифференциал
,
то изменение давления по ребру dz
есть дифференциал
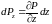 .
Тогда гидростатическое давление на
верхнюю грань равно
.
Тогда гидростатическое давление на
верхнюю грань равно
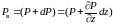 и проекция силы давления на ось z
и проекция силы давления на ось z
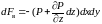 .Проекция
равнодействующей силы давления на ось
z
.Проекция
равнодействующей силы давления на ось
z
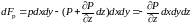
Сумма
проекций силы тяжести и силы давления
на ось z
равна 0, т.е.
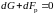
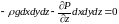 .Так
как объем параллелепипеда
.Так
как объем параллелепипеда
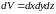 не равен нулю, то
не равен нулю, то
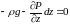 .Проекции
сил тяжести на оси x
и y
равны нулю. Поэтому для оси x
по аналогии получим
.Проекции
сил тяжести на оси x
и y
равны нулю. Поэтому для оси x
по аналогии получим
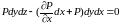 или
или
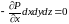 ;
;
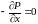
Аналогично
для оси y
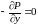
Итак
получили систему уравнений,
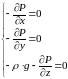 ,
которая называется системой дифференциальных
уравнений Эйлера. При интегрировании
данной системы получается основное
уравнение гидростатики.
,
которая называется системой дифференциальных
уравнений Эйлера. При интегрировании
данной системы получается основное
уравнение гидростатики.
6.Основное ур-е гидростатики.
Так
как в системе уравнений Эйлера частные
производные
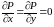 ,
то частная производная
может быть заменена на полную производную
,
то частная производная
может быть заменена на полную производную
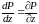 .
.
Тогда
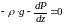 .
.
Разделяя
переменные, получим
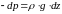 ,
интегрируя
,
интегрируя
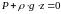 или
или
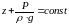

Для двух произвольных горизонтальных плоскостей 1 и 2 уравнение запишем:
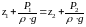 – это
основное уравнение гидростатики.
Для рисунка
– это
основное уравнение гидростатики.
Для рисунка
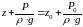 или
или
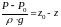
Член
z
называется нивелирной высотой или
геодезическим напором. Ее размерность
[м]. Величину
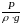 называют напором давления или
пьезометрическим напором.
называют напором давления или
пьезометрическим напором.
Согласно основному уравнению гидростатики, для любой точки покоящейся жидкости сумма нивелирной высоты и пьезометрического напора есть величина постоянная. Нивелирная высота также называется геометрическим (высотным) напором.
Основное
уравнение можно записать и в форме
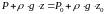
или
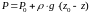 .
Это – закон Паскаля, согласно которому
давление, создаваемое в любой точке
покоящейся несжимаемой жидкости,
передается одинаково всем точкам ее
объема.
.
Это – закон Паскаля, согласно которому
давление, создаваемое в любой точке
покоящейся несжимаемой жидкости,
передается одинаково всем точкам ее
объема.
Действительно, при любом изменении давления P0 в точке z0 давление P во всякой другой точке жидкости изменится на столько же.
Следствие:
сила давления P
на горизонтальное дно сосуда не зависит
от формы сосуда, а определяется лишь
плотностью жидкости и ее уровнем над
дном H:
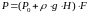
Для
вертикальной стенки P
изменяется по высоте, а сила
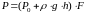 ,
где h
– расстояние от верхнего уровня жидкости
до центра тяжести площади F.
,
где h
– расстояние от верхнего уровня жидкости
до центра тяжести площади F.
Точка приложения равнодействующей P называется центром давления. Эта точка расположена ниже центра тяжести.
Самостоятельно про сообщающиеся сосуды и гидравлические машины.
7.Ур-е Паскаля. Практические приложения з-нов гидростатики.
Основное уравнение можно записать и в форме или . Это – закон Паскаля, согласно которому давление, создаваемое в любой точке покоящейся несжимаемой жидкости, передается одинаково всем точкам ее объема. Действительно, при любом изменении давления P0 в точке z0 давление P во всякой другой точке жидкости изменится на столько же. Следствие: сила давления P на горизонтальное дно сосуда не зависит от формы сосуда, а определяется лишь плотностью жидкости и ее уровнем над дном H: Для вертикальной стенки P изменяется по высоте, а сила , где h – расстояние от верхнего уровня жидкости до центра тяжести площади F.
Точка приложения равнодействующей P называется центром давления. Эта точка расположена ниже центра тяжести.
Самостоятельно про сообщающиеся сосуды и гидравлические машины.
Ур-е Паскаля также применяется для рсчета сообщ-ся сосудов,в частности гидравлического пресса.
