1. Предмет физики. Физическая модель. Классическая механика. Кинематика. Система отсчёта. Методы задания материальной точки.Связь координатного и векторного методов. Описание движения в классической механике.

Фи́зика (от греч. φύσις — природа) — область естествознания, наука, изучающая наиболее общие и фундаментальные закономерности, определяющие строение и развитие мира (материального мира, Вселенной).

Это наука о природе в самом общем смысле. Она изучает вещество (материю) и энергию и фундаментальные взаимодействия природы, управляющие движением тел, а также строение Вселенной вообще (космология).

Физической моделью процесса или явления называется его математическая модель, составленная из идеальных физических объектов. Изучением физических моделей, самих по себе, занимается теоретическая физика.

Простейшей физической моделью в классической механике является материальная точка. Несколько более сложные модели: идеальный газ, идеальная жидкость.

В лекции: Моделью называется совокупность черт и характеристик явлений, необходимых для его описания. Материальной точкой(частицей) наз-ся тело, размером которого можно пренебречь. Абсолютно твёрдым телом наз-ся тело, деформацией которого можно пренебречь.

Класси́ческая меха́ника — вид механики (раздела физики, изучающего законы изменения положений тел в пространстве со временем и причины, его вызывающие), основанный на законах Ньютона и принципе относительности Галилея. В ней изучаются законы движения макроскопических тел, скорости которых малы по сравнению со скоростью света в вакууме. Поэтому её часто называют «ньютоновой механикой».

Классическая механика подразделяется на:

• статику (которая рассматривает равновесие тел);

• кинематику (которая изучает геометрическое свойство движения тел без рассмотрения его причин);

• динамику (которая рассматривает движение тел с учётом вызывающих его причин).

Система отсчёта — это совокупность тела отсчёта, связанной с ним системы координат и системы отсчёта времени, по отношению к которым рассматривается движение (или равновесие) каких-либо материальных точек или тел

Методы задания материальной точки.

Рис. 1

1. Естественный способ. Этим способом пользуются, если из­вестна траектория движения точки. Траекторией называется совокуп­ность точек пространства, через которые проходит движущаяся мате­риальная частица. Это линия, которую она вычерчивает в пространстве. При есте­ст­венном способе необходимо задать (рис. 1):

а) траекторию движения (отно­си­тель­но какой-либо системы коор­динат);

б) произвольную точку на ней нуль, от которого отсчитывают расстояние S до движущейся частицы вдоль траектории;

в) положительное направление от­счета S (при смещении точки М в противоположном направлении S  отрицательно);

г) начало отсчета времени t;

д) функцию S(t), которая называется законом движения**) точки.

2. Координатный способ. Это наиболее универсальный и ис­черпывающий способ описания движения. Он предполагает задание:

а) системы координат (не обязательно декартовой) q1, q2, q3;

б) начало отсчета времени t;

в) закона движения точки, т.е. функций q1(t), q2(t), q3(t).

 Говоря о координатах точки, мы всегда будем иметь в виду (если не оговорено противное) ее декартовы координаты.

3. Векторный способ. Положение точки в пространстве может быть определено также и радиус-вектором, проведенным из некоторо­го начала в данную точку (рис. 2). В этом случае для описания дви­жения необходимо задать:

а) начало отсчета радиус-вектора r;

б) начало отсчета времени t;

в) закон движения точки r(t).

Поскольку задание одной векторной величины r эквивалентно заданию трех ее проекций x, y, z на оси координат, от век­торного способа легко перейти к коорди­натному. Если ввести единичные векторы i, j, k ( i = j = k = 1), направленные соответственно вдоль осей x, y и z (рис. 2), то, очевидно, закон движения может быть представлен в виде*)

r(t) = x(t)i +y(t)j+z(t)k.                                                                     

Преимущество векторной формы записи перед координатной в компактности (вместо трех величин оперируют с одной) и часто в большей наглядности.

Связь между координатным и векторным способами: ,

( – орты – единичные вектора, сонаправленные с какой-либо осью)

модуль , направляющие косинусы:  и т.д.

2. Криволинейное движение. Средняя и мгновенная скорость. Равнопеременное движение.

Криволинейное движение – это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу). Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д. В общем случае скорость при криволинейном движении изменяется по величине и по направлению.

Криволинейное движение материальной точки считается равномерным движением, если модуль скорости постоянен (например, равномерное движение по окружности), и равноускоренным, если модуль и направление скорости изменяется (например, движение тела, брошенного под углом к горизонту).

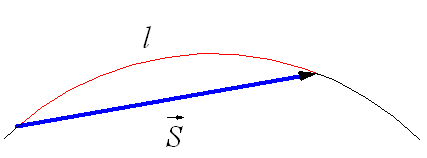Траектория и вектор перемещения при криволинейном движении.

При движении по криволинейной траектории вектор перемещения  направлен по хорде (рис. 1.19), а l – длина траектории. Мгновенная скорость движения тела (то есть скорость тела в данной точке траектории) направлена по касательной в той точке траектории, где в данный момент находится движущееся тело (рис. 1.20).

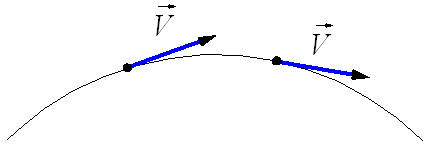.Мгновенная скорость при криволинейном движении.

Криволинейное движение – это всегда ускоренное движение. То естьускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости. Изменение величины скорости за единицу времени – это тангенциальное ускорение:

или Где v_τ, v₀ – величины скоростей в момент времени t₀ + Δt и t₀соответственно.

Тангенциальное ускорение в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему.

Нормальное ускорение - это изменение скорости по направлению за единицу времени:

Нормальное ускорение направлено по радиусу кривизны траектории (к оси вращения). Нормальное ускорение перпендикулярно направлению скорости.

Центростремительное ускорение – это нормальное ускорение при равномерном движении по окружности.

Полное ускорение при равнопеременном криволинейном движении тела равно:

Движение тела по криволинейной траектории можно приближённо представить как движение по дугам некоторых окружностей

Средняя и мгновенная скорость

Физическая величина, которая характеризует быстроту изменения координаты – скорость ( ).

Средняя скорость движения – это физическая величина, равная отношению вектора перемещения точки к интервалу времени, за который это перемещение произошло.

.

Средняя скорость – это величина, численно равная перемещению в единицу времени..

Направление вектора средней скорость всегда совпадает с направлением вектора перемещения:

Если точка движется прямолинейно в одном направлении , то S = | | = |x – x₀|.

Следовательно, модуль средней скорости по пути равен:

В международной системе единиц (СИ) скорость измеряется в метрах в секунду:

В системе единиц СГС (название по первым буквам трех основных единиц: сантиметр, грамм, секунда) скорость измеряется в сантиметрах в секунду:

Мгновенной скоростью  _мгн называется скорость в данный момент времени.

Мгновенная скорость определяется как предел отношения вектора перемещения к интервалу времени, за который это перемещение происходит, при стремлении интервала времени к нулю:

.

С точки зрения математики формула представляет собой определение первой производной по времени от радиус-вектора:

 (или  ).

Вектор скорости, как и любой вектор, можно задавать тремя компонентами по осям координат:

, (4)

т.е. компоненты вектора скорости выражаются производными по времени от соответствующих координат точки.

Примечание. Если известен вид функций, выражающих зависимость координат от времени, то компоненты скорости получим, дифференцируя эти функции по времени. Наоборот, если известно, как компоненты скорости точки зависят от времени, то при помощи обратной операции – интегрирования – мы найдем вид функций, выражающих зависимость координат от времени (см. примечание в § 7).

Вектор мгновенной скорости направлен по касательной к траектории (рис. 12). Исходя этого, можно дать следующее определение траектории:

Траектория – это линия, касательная к каждой точке которой совпадает с направлением вектора скорости в этих точках.

По характеру изменения скорости механические движения классифицируются на равномерные и неравномерные.

При равномерном движении модуль скорости в любой момент времени – величина постоянная:

| _cp| = | _мгн| = const   | | = const

При неравномерном (переменном) движении модуль скорости изменя-ется:

– Переменное движение, при котором модуль скорости увеличивается, (v > v₀) – это ускоренное движение.

– Переменное движение, при котором модуль скорости уменьшается (v < v₀) – это замедленное движение.

Равнопеременное движение