Нахождение расстояние от точки до плоскости.
Расстояние
от точки до прямой – это длина
перпендикуляра, опущенного из точки
к
данной плоскости:
Формула очень похожа на формулу «плоской» геометрии расстояния от точки до прямой.
Расстояние
от точки
до
плоскости 
выражается
формулой
.
Пример
Найти
расстояние от точки 
до
плоскости 
Решение:
анализировать тут нечего, главное, не
допустить ошибку в вычислениях:
Ответ: 
Билет #35 Канонические уравнения прямой
Если
известна некоторая точка пространства 
,
принадлежащая прямой, и направляющий
вектор 
данной
прямой, то канонические уравнения
этой прямой выражаются формулами:
Приведённая
запись предполагает, что координаты
направляющего вектора 
не
равны нулю.
Пример
Составить
канонические уравнения прямой по
точке 
и
направляющему вектору 
Решение:
Канонические уравнения прямой составим
по формуле:
Ответ: 
Что
следует отметить в этом очень простом
примере? Полученные уравнения НЕ НАДО
сокращать на единицу: 
.
Сократить, точнее, можно, но это непривычно
режет глаз и создаёт неудобства в ходе
решения задач.
На всякий случай смотрим на знаменатели уравнений и сверяемся – правильно ли там записаны координаты направляющего вектора Данный совет очень важен, поскольку позволяет полностью исключить ошибку по невнимательности. Никто не застрахован, а вдруг неправильно переписали?
Далее
подставляем координаты точки
в
найденные уравнения:
Получены верные равенства, значит, координаты точки удовлетворяют нашим уравнениям, и сама точка действительно принадлежит данной прямой.
Проверка очень легко выполняется устно.
В
ряде задач требуется найти какую-нибудь
другую точку 
,
принадлежащую данной прямой.
Берём
полученные уравнения
и
мысленно «отщипываем», например, левый
кусочек: 
.
Теперь этот кусочек приравниваем к
любому числу ,
например, к единице: 
.
Так как
,
то и два других «куска» тоже должны быть
равны единице. По сути, нужно решить
систему:
Проверим,
удовлетворяет ли найденная
точка 
уравнениям
:
Получены верные равенства, значит, точка действительно лежит на данной прямой.
Как составить уравнения пространственной прямой по двум точкам?
Если
известны две точки пространства 
,
то уравнения прямой, проходящей через
данные точки, выражаются формулами:
Унылый
частный случай предыдущего параграфа.
И в самом деле, вектор 
является
направляющим вектором прямой.
По возможности, рекомендую не пользоваться данными формулами. Хорошо-то оно, всё хорошо, но только до тех пор, пока знаменатели без нулей. Не буду объяснять все тонкости, но рекомендую придерживаться следующего алгоритма решения:
Пример
Составить
уравнения прямой, проходящей через
точки 
.
Решение:
Найдём направляющий вектор прямой:
Уравнения
прямой составим по точке 
(можно
было выбрать точку 
)
и направляющему вектору 
:
Ответ: 
Прямая, заданная пересечением двух плоскостей
Если
плоскости 
пересекаются,
то
система линейных уравнений
задаёт
прямую в пространстве.
То есть прямая задана уравнениями двух плоскостей. Типовая и распространенная задача состоит в том, чтобы переписать уравнения прямой в каноническом виде:
Пример
Записать
канонические уравнения прямой 
Решение: Чтобы составить канонические уравнения прямой, необходимо знать точку и направляющий вектор. А у нас даны уравнения двух плоскостей….
1)
Сначала найдём какую-либо точку,
принадлежащую данной прямой. Как это
сделать? В системе уравнений нужно
обнулить какую-нибудь координату.
Пусть 
,
тогда получаем систему двух линейных
уравнений с двумя неизвестными: 
.
Почленно складываем уравнения и находим
решение системы:
Таким
образом, точка 
принадлежит
данной прямой. Обратите внимание на
следующий технический момент: желательно
найти точку с целыми координатами.
Если бы в системе мы обнулили «икс» или
«зет», то не факт, что получилась бы
«хорошая» точка без дробных координат.
Такой анализ и подбор точки следует
проводить мысленно или на черновике.
Выполним
проверку: подставим координаты точки
в
исходную систему уравнений: 
.
Получены верные равенства, значит,
действительно 
.
2)
Как найти направляющий вектор прямой?
Его нахождение наглядно демонстрирует
следующий схематический чертёж:
Направляющий
вектор нашей прямой ортогонален
нормальным векторам плоскостей. А
если 
,
то вектор «пэ» найдём как векторное
произведение векторов
нормали: 
.
Из
уравнений плоскостей 
снимаем
их векторы нормали:
И
находим направляющий вектор прямой:
3)
Составим канонические уравнения прямой
по точке
и
направляющему вектору
:
Ответ: 
БИЛЕТ
#36
БИЛЕТ #37
БИЛЕТ #38
БИЛЕТ
#39
БИЛЕТ
#40
БИЛЕТ #41
Квадратичные формы: определения, примеры, матрица квадратичной формы и ее свойства
Определение 1. Квадратичной формой f от n неизвестных x1, x2,…xn называется сумма, каждый член которой является или квадратом одного из этих неизвестных, или произведение двух разных неизвестных. Квадратичная форма называется действительной или комплексной в зависимости от того, являются ли ее коэффициенты действительными или же могут быть любыми комплексными числами.
Определение 2. Пусть e1, ..., en — базис в L. И пусть для вектора x из L задано разложение x = x1·e1+x2·e2+ ...+ xn· en.
Тогда для квадратичной формы k(x) справедливо представление:
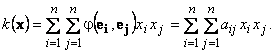
Здесь φ(ei , ej ) — значение полярной для k(x) билинейной формы φ(x , y).
Матрица A = {aij} называется матрицей квадратичной формы. Определённая таким образом матрица квадратичной формы является симметричной матрицей.
Определение
3.
Квадратичной
формой двух переменных называется
однородный многочлен второй степени
относительно этих переменных:
.
Квадратичная форма трех переменных:
Матрица
вида 
называется
матрицей квадратичной формы.
Квадратичная
форма имеет канонический вид 
тогда
и только тогда, когда её матрица имеет
диагональный вид 
.
. 
.
Свойства квадратичной формы:
1)Матрица квадратичной формы симметрическая
2)Симметрическая матрица с вещественными элементами имеет вещественные собственные числа.
3)Собственные векторы, соответствующие различным вещественным собственным числам, ортогональны.
В
ортонормированном базисе из собственных
векторов квадратичная форма имеет
канонический вид:
,
где 
и 
-
собственные числа матрицы квадратичной
формы
.
При этом формулы преобразования координат
имеют вид: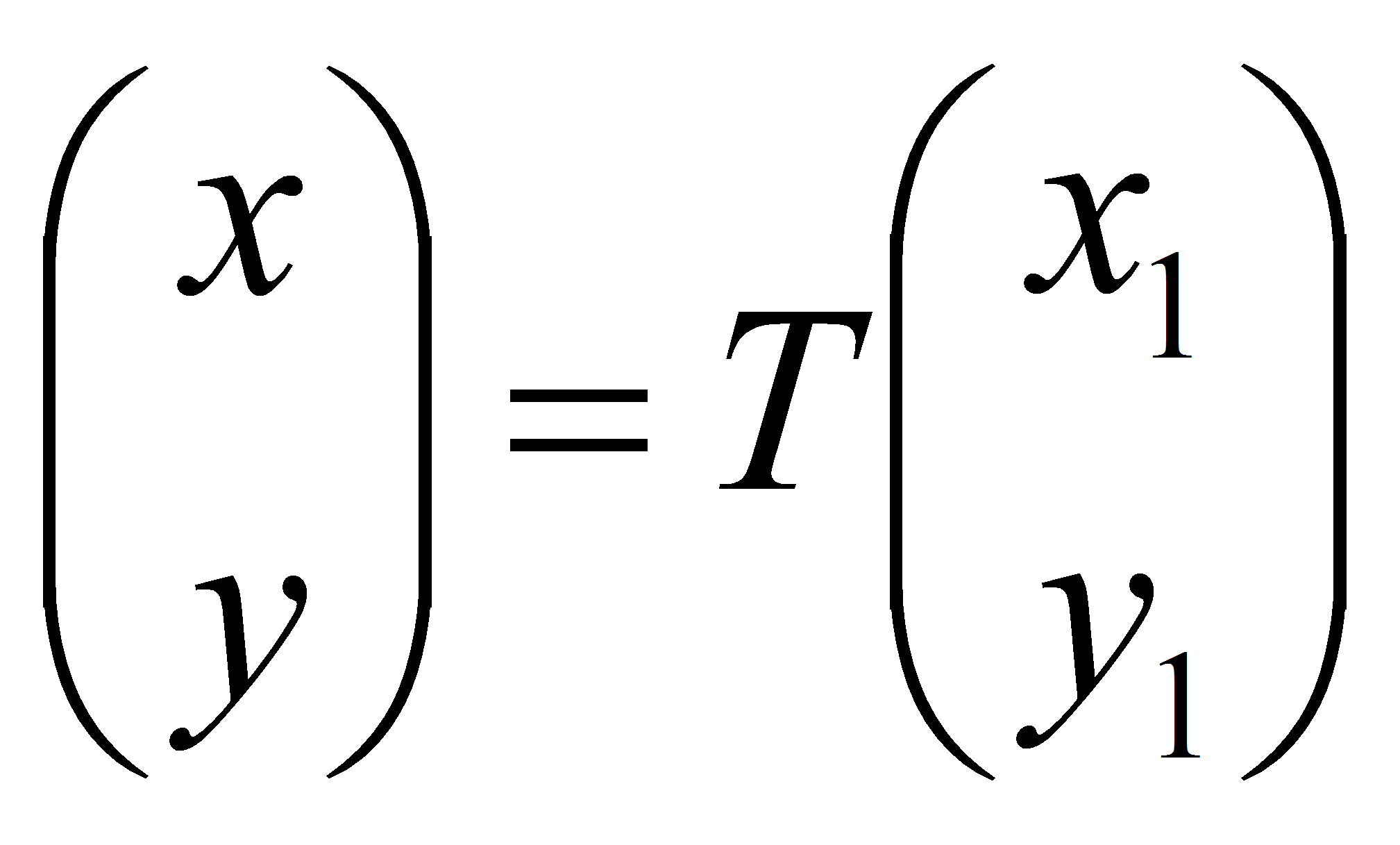 
,
где первый и второй столбец матрицы
перехода T являются
координатами соответственно первого
и второго собственных векторов матрицы А,
причем определитель матрицы T>0.
Матрицу
называют
матрицей квадратичной формы в данном
базисе. В случае, если характеристика
поля
не
равна 2, можно считать, что матрица
квадратичной формы симметрична, то
есть
.Для любой квадратичной формы существует единственная симметричная билинейная форма , такая, что
.
Билинейную форму 
называют полярной к 
,
она может быть вычислена по формуле
Матрица квадратичной формы в произвольном базисе совпадает с матрицей полярной ей билинейной формы в том же базисе.
Если матрица квадратичной формы имеет полный ранг, то квадратичную форму называют невырожденной, иначе — вырожденной.
Квадратичная форма называется положительно (отрицательно) определённой, если для любого
выполнено
неравенство 
.
Положительно определённые и отрицательно
определённые формы называются
знакоопределёнными.Квадратичная форма
называется знакопеременной,
если она принимает как положительные,
так и отрицательные значения.Квадратичная форма называется положительно (отрицательно) полуопределенной, если
для
любого 
.
БИЛЕТ #42 Приведение квадратичной формы к каноническому и нормальному видам. Метод Лагранжа.
Теорема: Всякая квадратичная форма с помощью линейного невырожденного преобразования (преобразования координат) может быть приведена к каноническому виду.
Доказательство: Пусть (а) – квадратичная форма, заданная на пространстве Ln . Пусть в Ln задан базис е и пусть в этом базисе (а) = хТ А х . Матрица А –симметрическая, поэтому по теореме 60 существует такая ортогональная матрица Т, что матрица А1 = Т–1АТ будет диагональной, причём на диагонали стоят собственные значения матрицы А (они все – действительные числа). Так как ортогональная матрица невырожденная, то существует такой базис е1, что Т будет матрицей перехода от базиса е к базису е1. Так как для ортогональной матрицы Т –1 = Т Т, то А1 – матрица данной формы в базисе е1. Итак, в базисе е1 данная форма имеет канонический вид.
БИЛЕТ #43
Закон инерции. Понятие о приведении квадратичной формы к главным осям.
Канонический вид квадратичной формы не является однозначно определенным, так как одна и та же квадратичная форма может быть приведена к каноническому виду многими способами. Однако полученные различными способами канонические формы обладают рядом общих свойств. Одно из этих свойств формулируется в виде теоремы.
Закон инерции. Пусть k(x) — квадратичная форма, заданная в пространстве арифметических векторов Rn.
В пространстве Rn существует канонический базис квадратичной формы, базис, в котором матрица квадратичной формы является диагональной.
В этом базисе квадратичная форма имеет канонический вид
k(x) = λ1x12 + λ2x22 + ... + λnxn2.
Числа λ1, λ2, ... , λn — канонические коэффициенты квадратичной формы.
Закон инерции квадратичных форм гласит: число положительных, отрицательных и нулевых канонических коэффициентов квадратичной формы не зависит от преобразования, с помощью которого квадратичная форма приводится к каноническому виду.
Число положительных канонических коэффициентов квадратичной формы называется положительным индексом инерции квадратичной формы. Число отрицательных канонических коэффициентов квадратичной формы называется отрицательным индексом инерции квадратичной формы. Разность между положительным и отрицательным индексом квадратичной формы называется сигнатурой квадратичной формы. Число ненулевых канонических коэффициентов называется рангом квадратичной формы.
Пример: Пусть k(x) = x12 + x22— квадратичная форма в пространствеR2.
Пусть e1= (1, 0), e2= (0, 1) — базис в R2. Матрица A квадратичной формы диагональна:
Это означает, что базис e1= (1, 0), e2= (0, 1) — канонический базис квадратичной формы.
Квадратичная форма k(x) = x12 + x22 имеет канонический вид, числа 1, 1 — канонические коэффициенты квадратичной формы, положительный индекс инерции квадратичной формы равен 2, инерции квадратичной формы равен 0, сигнатура квадратичной формы равна 2 − 0 = 2, ранг квадратичной формы равен 2.
Понятие о приведении квадратичной формы к главным осям
БИЛЕТ #44 Положительно и отрицательно определенные квадратичные формы. Критерий Сильвестра.
1. Невырожденная квадратичная форма является положительно определенной тогда и только тогда, когда:
либо все главные (угловые) миноры матрицы квадратичной формы положительны (критерий Сильвестра);
либо все собственные значения матрицы квадратичной формы положительны.
Пример:
И
сследовать
на знакоопределенность квадратичную
форму
Получаем матрицу квадратичной формы А:
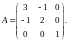
Далее решаем по критерию Сильвестра:
квадратичная форма является положительно определенной.
2. Невырожденная квадратичная форма является отрицательно определенной тогда и только тогда, когда
либо все главные миноры матрицы квадратичной формы четного порядка положительны, а нечетного - отрицательны (критерий Сильвестра);
либо все собственные значения матрицы квадратичной формы отрицательны.
Пример:
И
сследовать
на знакоопределенность квадратичную
форму:
П
олучаем
матрицу квадратичной формы А:
Д
алее
по критерию Сильвестра:
Квадратичная форма является отрицательно определенной
Для того, чтобы определить знакоопределенность матрицы, нужно воспользоваться критерием Сильвестра, то есть составить и решить характеристическое уравнение матрицы:
Характеристическим уравнением матрицы
называется уравнение
БИЛЕТ #45 Кривые второго порядка. Канонические уравнения. Парабола: форма и свойства. Фокус, директриса.
Кривая второго порядка — геометрическое место точек плоскости, прямоугольные координаты которых удовлетворяют уравнению вида
в котором, по крайней
мере, один из коэффициентов 
отличен
от нуля.
Кривыми второго порядка называют эллипс, параболу и гиперболу.
Вид кривой |
Каноническое уравнение |
Инварианты |
Невырожденные кривые (Δ ≠ 0) |
||
Эллипс |
|
|
Гипербола |
|
|
Парабола |
|
|
|
||
Канонические уравнения кривых второго порядка
окружность
радиуса 
,
начало координат – центр симметрии
(рис. 11);
эллипс,
осевая симметрия (рис. 11);
Рис. 11. Эллипс и окружность
гипербола,
пересекает ось 
(рис.
12), осевая симметрия;
гипербола,
пересекает ось 
(рис.
12), осевая симметрия;
Рис. 12. Сопряженные гиперболы
парабола, 
параметр,
вершина в начале координат, ветви
направлены вверх, ось
ось
симметрии (рис. 13);
парабола,
параметр,
вершина в начале координат, ветви
направлены вниз, ось
ось
симметрии (рис. 13);
парабола,
параметр,
вершина в начале координат, ветви
направлены вправо, ось
ось
симметрии (рис. 13) ;
парабола,
параметр,
вершина в начале координат, ветви
направлены влево, ось
ось
симметрии (рис. 13) .
Рис. 13. Параболы
Парабола. Параболой называется геометрическое место точек, каждая из которых одинаково удалена от заданной фиксированной точки и от заданной фиксированной прямой. Точка, о которой идет речь в определении, называется фокусом параболы, а прямая - ее директрисой.
Простейшее уравнение параболы
y2 = 2px. (*)
Входящая в это уравнение величина p называется параметром параболы. Параметр параболы равен расстоянию от директрисы параболы до ее фокуса.
Координаты
фокуса F параболы
(*) 
.
(фокус параболы лежит на ее оси симметрии)
Уравнение директрисы параболы (*)
Эксцентриситет параболы e = 1.
y2 =
2px (p >
0)
БИЛЕТ
#46
БИЛЕТ #47
БИЛЕТ
#48
БИЛЕТ #49
БИЛЕТ #50
