Ответы на вопросы к подготовке по Линейной алгебре 2014-2015.

1. Системы линейных уравнений: определения, классификация, примеры.

2. Однородные и неоднородные системы уравнений. Свойства множеств их решений. Примеры.

3. Решение систем линейных уравнений в случаях, когда матрица коэффициентов треугольная или ступенчатая.

4. Эквивалентные (равносильные) системы. Элементарные преобразования строк расширенной матрицы системы.

5. Алгоритм Гаусса решения систем линейных уравнений (общий случай).

6. Фундаментальная система решений: определение, применение.

7. Линейно зависимые системы векторов: определение, примеры, свойства. Критерий линейной зависимости.

8. Линейно независимые системы векторов: определение, примеры, свойства.

9. Координаты вектора: определение, примеры, свойства.

10. Линейные операции над матрицами, транспонирование матриц: определение, примеры, свойства.

11. Умножение матриц, транспонирование матриц: определение, примеры, свойства.

12. Обратная матрица: определение, свойства, способ отыскания. Решение матричных уравнений.

13. Формулы вычисления определителей второго и третьего порядка, важнейшие свойства.

14. Основные свойства определителя. Алгебраические дополнения. Общее определение.

15. Разложения определителей по строкам и столбцам. Способы вычисления определителей.

16. Применение определителей к системам линейных уравнений: теорема Крамера.

17. Условия существования обратной матрицы, формула для вычисления.

18. Ранг матрицы: определение, свойства, способы вычисления.

19. Миноры матрицы: применение к исследованию зависимости строк и столбцов: теорема о ранге матрицы. Условия вырожденности матриц.

20. Ранг матрицы: свойства, применение к системам линейных уравнений: теорема Кронекера – Капелли.

21. Модель бездефицитной торговли.

22. Собственные векторы и собственные значения матриц: определения, свойства, примеры.

23. Нахождение собственных векторов и собственных значений матриц.

24. Межотраслевой баланс. Уравнения Леонтьева.

25. Понятие продуктивности. Условия продуктивности матриц. Примеры.

26. Теорема Перрона – Фробениуса, ее использование для исследования продуктивности. Запас продуктивности.

27. Модель равновесных цен.

28. Понятие линейного пространства. Примеры линейных пространств.

29. Понятия базиса, размерности. Основные свойства базиса.

30. Векторы на прямой, на плоскости, в пространстве: операции и их свойства.

31. Геометрический смысл линейной зависимости. Базисы и системы координат.

32. Уравнение множества точек на плоскости и в пространстве: определение, примеры.

33. Геометрическая интерпретация систем линейных уравнений: плоскость в пространстве. Различные формы уравнений плоскости в пространстве.

34. Взаимное расположение плоскостей в пространстве. Расстояние от точки до плоскости.

35. Геометрическая интерпретация систем линейных уравнений: прямая в пространстве. Различные формы уравнений прямой в пространстве.

36. Взаимное расположение прямой и плоскости в пространстве.

37. Взаимное расположение прямых в пространстве.

38. Векторное произведение векторов: определение, свойства и применения.

39. Смешанное произведение векторов: определение, свойства и применения.

40. Линейные объекты в Rn: прямые, отрезки, гиперплоскости, полупространства.

41. Квадратичные формы: определения, примеры, матрица квадратичной формы и ее свойства.

42. Приведение квадратичной формы к каноническому и нормальному видам. Метод Лагранжа.

43. Закон инерции. Понятие о приведении квадратичной формы к главным осям.

44. Положительно и отрицательно определенные квадратичные формы. Критерий Сильвестра.

45. Кривые второго порядка. Канонические уравнения. Парабола: форма и свойства. Фокус, директриса.

46. Кривые второго порядка. Гипербола: форма и свойства. Фокусы, директрисы.

47. Кривые второго порядка. Эллипс: форма и свойства. Фокусы, директрисы.

48. Поверхности второго прядка. Канонические уравнения. Эллипсоиды.

49. Поверхности второго прядка. Гиперболоиды и конусы.

50. Поверхности второго прядка. Параболоиды и цилиндры.

БИЛЕТ #1 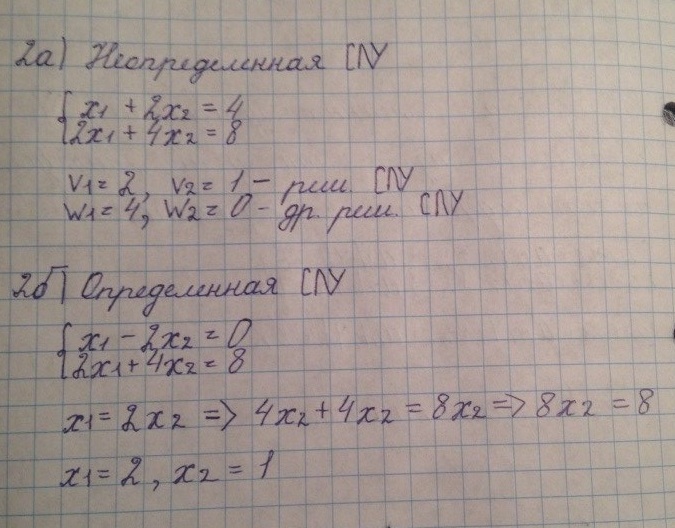БИЛЕТ #2 БИЛЕТ #3 БИЛЕТ #4 #5

БИЛЕТ #6 Определение. Любые линейно независимых решений линейного однородного дифференциального уравнения -ного порядка называется фундаментальной системой решений этого уравнения.

Применение. Термин ФСР используется для обозначения базиса в пространстве решений системы линейных однородных алгебраических уравнений. Через элементы ФСР оказывается возможным выразить , и при том единственным образом, элементы некоторого бесконечного множества.

Если ранг матрицы системы однородной СЛУ равен r , то такая СЛУ имеет n−r линейно независимых решений: φ 1 , φ 2 ,..., φ n−r .

Любая совокупность n−r линейно независимых решений однородной СЛУ называется фундаментальной системой (или совокупностью) решений данной СЛУ. Часто вместо словосочетания "фундаментальная система решений" используют аббревиатуру "ФСР". Если решения φ 1 , φ 2 ,..., φ n−r образуют ФСР, и X – матрица переменных данной СЛУ, то общее решение СЛУ можно представить в таком виде:

X=C 1 ⋅φ 1 +C 2 ⋅φ 2 +…+C n−r ⋅φ n−r ,

где C 1 , C 2 ,..., C n−r – произвольные постоянные.

БИЛЕТ #7 #8 БИЛЕТ #9

БИЛЕТ #10

Некоторые операции над матрицами, такие как сложение и вычитание, допускаются только для матриц одинакового размера.

Равные матрицы

Определение

Две матрицы называются равными, если они имеют одинаковые размеры и их соответствующие элементы равны:

Пример

 . Эти матрицы равны, т.к. равны их размеры:   и  , а также соответствующие элементы:  ; 

Пример

Задание. Пусть задана матрица   . Найти все элементы матрицы  , если известно, что она равна матрице 

Решение. Так как матрицы   и   равны, то равны и их соответствующие элементы, т.е.

Ответ. 

Произведение матрицы на число

Определение

Произведением матрицы на число называется матрица, полученная из исходной умножением каждого ее элемента на заданное число.

Пример

Задание. Пусть   . Найти матрицу  .

Решение. 

Ответ. 

Подробная теория про умножение марицы на число по ссылке.

Сумма матриц

Определение

Суммой матриц   и   одного размера называется матрица   такого же размера, получаемая из исходных путем сложения соответствующих элементов.

Пример

Задание. Найти  , если  , 

Решение. 

Ответ. 

Операции умножение матрицы на число и сумма матриц называются линейными.

Свойства линейных операций:

Везде далее матрицы  ,   и   - матрицы одного размера.

1. Ассоциативность 

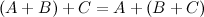
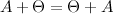2. , где 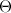  - нулевая матрица соответствующего размера.

3. 

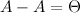
4. Коммутативность 

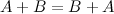
5. Дистрибутивность 

6. 

7. 

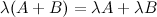
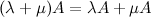
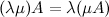
Произведение двух матриц

Определение

Произведением матрицы   на матрицу   называется матрица   такая, что элемент матрицы  , стоящий в  -ой строке и  -ом столбце, т.е. элемент  , равен сумме произведений элементов  -ой строки матрицы   на соответствующие элементы  -ого столбца матрицы  .

Пример

Задание. Найти  , если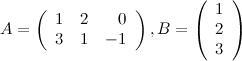 

Решение. Так как  , а  , то в результате получим матрицу размера  , т.е. матрицу вида   . Найдем элементы данной матрицы:

Таким образом, получаем, что:

Все вычисления можно было сделать в более компактном виде:

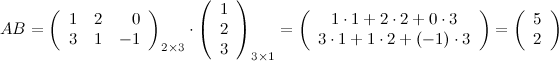
Ответ. 

Свойства произведения матриц:

1. Ассоциативность 

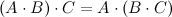
2. Ассоциативность по умножению 

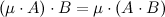
3. Дистрибутивность  , 

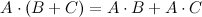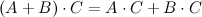
4. Умножение на единичную матрицу 

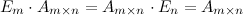
5. В общем случае умножение матриц не коммутативно, т.е. 

6. 

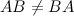
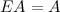
Транспонирование матриц

Определение

Транспонирование матрицы - это операция над матрицей, когда ее строки становятся столбцами с теми же номерами.

Пример

Задание. Найти транспонированную матрицу  , если 

Решение.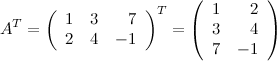 

Свойства транспонирования матриц:

1. 

2. 

3. 

4. 

БИЛЕТ #11 Транспонирование матриц

Матрица А^Т размером n*m называется транспонированной к матрице А размером n*m, если строки матрицы А^Т являются столбцами матрицы А с сохранением их порядка

A= A^T=

Cвойства

(A^T)^T=A

(А+В)^Т=А^Т+В^Т

( *A)^T= *A^T

(BV)^T=B^T*V^T

Умножение матриц

Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором. Произведением матрицы А размера m*n и матрицы В размера n*k называется матрица С размера m*k, каждый элемент с_ij, которой равен скалярному произведению вектора-строки на вектор-столбец.

C_ij=a_i*b_j

А= B=

A*B=

B*A=

Cвойства

A(BC)=(AB)C

A(B+C)=AB+AC

EA=A

0*A=0

k(AB)=(kA)B*(kB)A

AB BA

БИЛЕТ #12 Обратная матрица – такая матрица А^-1 при умножении на которую, исходная матрица А дает единичную Е

АА-1=Е

Обратная матрица есть только у квадратных матриц, чей определитель не равен 0

Свойства :

Det A^-1=1/detA

(AB)^-1=B^-1A^-1

(A^T)^-1=(A^-1)^T

(kA)^-1=k^-1*A^-1

E^-1=E

Способы нахождения:

1. методом Гаусса

Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A⁻¹.

2. Способом алгебраических преобразований и дополнений

Решение матричных уравнений

Уравнение вида AX=B cледует решать с помощью обратных матриц

Умножаем обе части уравнения на обратную матрицу

AX=C

A^-1AX=A^-1C

EX=A^-1C

X=A^-1C

Далее находим обратную матрицу и умножаем ее на матрицу С

БИЛЕТ #13 Формула вычисления определителя второго порядка:

=ad-bc

Формула вычисления определителя третьего порядка:

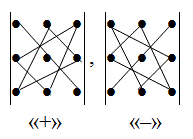
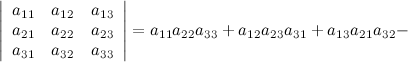
Свойства определителей:

1. Определитель не изменяется при транспонировании

2. При умножении элементов строки определителя на некоторое число весь определитель умножается на это число

3. Определитель, имеющий нулевую строку, равен 0. 

4. Определитель, имеющий две равные строки, равен 0.

5. Определитель, две строки которого пропорциональны, равен 0.

6. При перестановке двух любых столбцов (строк) определителя его знак меняется на противоположный, а абсолютная величина остается неизменной.

7. Определитель не изменится, если к любому его столбцу (строке) прибавить произвольную линейную комбинацию его столбцов (строк).

8. Определитель суммы двух квадратных матриц одного и того же порядка равен сумме всех различных определителей порядка n, которые могут получиться, если часть строк (столбцов) брать совпадающими с соответствующими строками (столбцами) матрицы А, а оставшуюся часть – совпадающими с соответствующими строками (столбцами) матрицы В.

Определитель произведения двух матриц равен произведению их определителей БИЛЕТ #14 Свойства определителя те же , что в №13

Алгебраические дополнения

Алгебраическим дополнением к элементу определителя -го порядка называется число , где к элементу определителя -го порядка называется определитель -го порядка, полученный из исходного вычеркиванием -той строки и -того столбца.

БИЛЕТ #15

Разложение определителя

По i-ой строке:

По j-ому столбцу:

По первой строке в матрице:

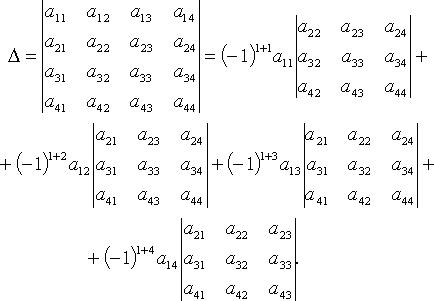
Способы вычисления определителей :

1. вычисление определителя двойного порядка

2. вычисление по правилу треугольника

3. путем алгебраических дополнений

4. путем разложения определителя по строке и столбцу

5. путем приведения определителя к треугольному виду

БИЛЕТ #16

Применение определителей к системам линейных уравнений: теорема Крамера. Теорема: Система n линейных уравнений с n неизвестными имеет единственное решение тогда и только тогда, когда определитель матрица А коэффициентов при неизвестных отличен от нуля, |A|=∆≠0; Значения неизвестных находятся по формулам Крамера: , где – определитель матрица, полученной из А заменой j-го столбца столбцом свободных членов.

Кратко алгоритм метода Крамера можно описать тремя шагами:

1)Находим определитель D исходной матрицы A.

2)В цикле от 1 до n заменяем i-ый столбец матрицы на столбец результатов B. Находим текущий определитель полученной матрицы.

3) находится делением на D: = / D. БИЛЕТ #17

Условия существования обратной матрицы, формула для вычисления. Матрица 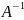называется обратной матрицей по отношению к матрице А, если А* = Е, где Е — единичная матрица n-го порядка. Обратная матрица может существовать только для квадратных матриц.

Теорема: Для невырожденной матрицы существует обратная матрица. ( Квадратная матрица называется невырожденной, если ее определитель отличен от нуля) Алгоритм нахождения обратной матрицы:

1. Определяют, квадратная ли матрица. Если нет, то обратной матрицы для нее не существует.

2. Вычисление определителя матрицы A. Если он не равен нулю, продолжаем решение, иначе - обратной матрицы не существует.

3. Нахождение транспонированной матрицы AT.

4. Определение алгебраических дополнений. Заменяют каждый элемент матрицы его алгебраическим дополнением.

5. Составление обратной матрицы из алгебраических дополнений: каждый элемент полученной матрицы делят на определитель исходной матрицы. Результирующая матрица является обратной для исходной матрицы.

6. Делают проверку: перемножают исходную и полученную матрицы. В результате должна получиться единичная матрица. Обратная матрица определяется по формуле:

Матрицу называют присоединенной для А. ( матрица из алгебраических дополнений)

БИЛЕТ #18

Ранг матрицы: определение, свойства, способы вычисления.

Число r называется рангом матрицы A, если:  1) в матрице A есть минор порядка r, отличный от нуля;  2) все миноры порядка (r+1) и выше, если они существуют, равны нулю.  Иначе, ранг матрицы – это наивысший порядок минора, отличного от нуля.  Из определения следует, что r – целое положительное число. Для нуль-матрицы считают ранг равным нулю. (Минором прямоугольной матрицы называется определитель, составленный из чисел, которые находятся на пересечении различных   строк и различных   столбцов матрицы. Число   называют порядком минора.)

Определение по методу Гаусса: Ранг матрицы – это число ненулевых строк в ее ступенчатом виде, то есть для нахождения ранга матрицы нужно с помощью преобразований привести матрицу к ступенчатому виду и сосчитать число ненулевых строк. Алгоритм нахождения ранга матрицы с помощью миноров: 1) необходимо начать перебор и вычисление миноров 2-го порядка. Если ВСЕ миноры 2-го порядка окажутся нулевыми, то ранг матрицы равен единице. Но это крайне маловероятно, рано или поздно (чаще всего рано), встретится ненулевой минор , и данный факт означает, что ранг матрицы не менее двух.

2)На следующем шаге последовательно перебираем и рассчитываем миноры 3-го порядка. Если ВСЕ эти миноры равны нулю, то ранг=2 . Если же встретился минор , то делаем вывод о том, что ранг матрицы не менее трёх и переходим к следующему шагу.

3)Перебор и вычисление миноров 4-го порядка. Если ВСЕ миноры 4-го порядка равны нулю, то ранг=3, если встретился минор , то ранг=4 .

Таким образом, ранг матрицы равен максимальному порядку ненулевого минора. Есть еще алгоритм окаймляющих миноров, но он мне не нравится. Так понятнее гораздо.

БИЛЕТ #19 Миноры матрицы: применение к исследованию зависимости строк и столбцов: теорема о ранге матрицы. Условия вырожденности матриц

Минор, определяющий ранг матрицы, называется Базисным минором. Строки и столбцы, формирующие БМ, называются базисными строками и столбцами.

Теорема о базисном миноре. Столбцы матрицы А, входящие в БМ, образуют линейно независимую систему. Любой столбец матрицы А линейно выражается через столбцы из БМ. Теорема о ранге матрицы. Ранг матрицы А равен максимальному числу линейно независимых столбцов (или равен рангу системы столбцов матрицы А). Система строк называется линейно зависимой, если существует их нетривиальная линейная комбинация, равная нулевой строке. Линейной комбинацией (ЛК) строк матрицы А называется выражение +…+ ЛК называется тривиальной, если все коэффициенты равны нулю одновременно.

Пример: Система строк   , линейно зависима, так как ЛК этих строк   равна нулевой строке. Вырожденной матрицей называется квадратная матрица А , если её определитель (Δ) равен нулю. В противном случае матрица А называется невырожденной. Эквивалентные условия: - Δ равен нулю - Строки или столбцы матрицы линейно зависимы. - Квадратная матрица A вырождена тогда и только тогда, когда существует ненулевой вектор x, такой, что Ax = 0. Иными словами, линейный оператор, соответствующий матрице в стандартном базисе, имеет ненулевое ядро.

БИЛЕТ #20 Ранг матрицы: свойства, применение к системам линейных уравнений: теорема Кронекера – Капелли. Теорема Кронекера-Капелли. СЛАУ совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.

Задание. При каких значениях   система 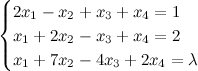  будет совместной?

Решение. Ранг матрицы равен количеству ненулевых строк после приведения этой матрицы к ступенчатому виду. Поэтому записываем расширенную матрицу системы   (слева от вертикальной черты находится матрица системы   ):

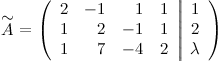
и с помощью элементарных преобразований приводим ее к ступенчатому виду. Для этого вначале от первой строки отнимаем две вторых строки, а от третьей вторую, в результате получаем:

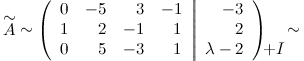
Третью строку складываем с первой:

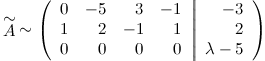
и меняем первую и вторую строки матрицы местами

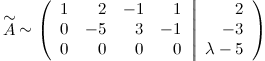
Матрица приведена к ступенчатому виду. Получаем, что  ,  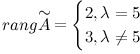 . Таким образом, при   система совместна, а при   - несовместна.

Свойства ранга матрицы: 1) Ранг матрицы, полученной трансплонированием, равен рагу исходной марицы 2) Ранг матрицы остается неизменным, если вычеркнуть или приписать нулевую стоку

БИЛЕТ #21 Модель бездефицитной торговли.

n стран образуют замкнутую экономическую систему

x_j ден. ед. – годовые затраты j-й страны на торговлю

x_ij ден. ед. – ее затраты на торговлю с i-ой страной

x_j = x_1j + x_2j + … + x_nj

x_ij/x_j = a_ij – доля ее затрат, приходящихся на закупку продукции i-ой страны: a_1j +a_2j +…+a_nj =1

a_ijx_j – выручка i-й страны в торговле с j-ой

y_i = a_i1x₁ + a_i2x₂ + … + a_inx_n – вся торговая выручка i-ой страны. 1≤ i ≤ n

Торговля i-ой страны бездефицитна, если y_i ≥ x_i

Бездефицитная торговля всех стран возможна, если существует y_i = x_i

БИЛЕТ #22 Собственные векторы и собственные значения матриц: определения, свойства, примеры.

Собственным вектором квадратной матрицы А порядка n называется ненулевой n-мерный

x₁

вектор-столбец x = x₂ такой, что Аx=λx, где λ – некоторое число. Число λ называется

…

x_n

собственным значением матрицы А. При этом говорят, что вектор x является собственным вектором матрицы А, принадлежащим собственному значению λ.

Пример:

1 2

А= 4 3

Соотношение выглядит следующим образом:

1 2 x₁ x₁

4 3 x₂ = λ x₂

Решаем характеристическое уравнение, корни которого будут собственными значениями матрицы:

1-λ 2

|А-λЕ|= 4 3-λ = λ²-4 λ-5=0

λ₁=5 и λ₂= -1 – собственные значения

К аждое полученное число подставляется в матричное равенство, после чего это равенство представляет собой СЛУ, решения которых будут собственные векторы, принадлежащие данному собственному числу.

(А- λ_1,2Е)X=0

1/2

Х₁= s 1 , s ≠0

-1

X₂= t 1 , t ≠0

Характеристическое уравнение может не иметь корней. Тогда у матрицы нет и собственных векторов.

БИЛЕТ #23

Нахождение собственных векторов и собственных значений матриц.

Алгоритм нахождения: вначале решается характеристическое уравнение, корни которого и будут собственными значениями матрицы; затем каждое полученное число подставляется в матричное равенство, после чего это равенство представляет собой СЛУ, решения которых будут собственные векторы, принадлежащие данному собственному числу.

БИЛЕТ #24

Межотраслевой баланс. Уравнения Леонтьева.

x_i = x_i1 + x_i2 + … + x_in + y_i – валовой продукт i-ой отрасли (1≤ i ≤ n) есть сумма промежуточного и конечного продуктов

x_ij – часть продукции i-ой отрасли, используемая на производственные нужды j-ой отрасли

Если ы определенном промежутке времени материальные издержки пропорциональны объему производства, то x_ij/x_j = a_ij = const – количество продукции i-ой отрасли, необходимое для производства единицы продукции j-ой отрасли.

А – матрица прямых затрат

x₁ y₁

X = … - вектор валового продукта; y = … - вектор конечного продукта

x_n y_n

x_i = a_i1x₁ + … + a_inx_n + y_i <=> X = Ax + y - уравнение Леонтьева (Л)

1≤ i ≤ n

БИЛЕТ #25

Понятие продуктивности. Условия продуктивности матриц. Примеры.

Матрица А называется продуктивной, если для любого y ≥0 существует x ≥0 – решение уравнения (Л)

( Л) <=> x – Аx = y <=> (E-A)x = y

Матрица А продуктивна <=> существует (E-A)^-1

(E-A)^-1≥0 => для любого y ≥0 x=(E-A)^-1y ≥0

= > беря по очереди y = e₁, e₂, … , e_n ≥0 получаем столбцы матрицы (E-A)^-1:

столбцы единичной матрицы

(E-A|E) ^Э2,Э2,Э3 (E|(E-A)^-1)

(E-A)^-1≥0

Теорема Перрона-Фробениуса:

1. Максимальное по модулю собственное значение матрицы А≥0: λ_А≥0

2. При собственном значении λ_А существует неотрицательный собственный вектор

3. Матрица продуктивна <=> λ_А<1

Запас продуктивности – α_А= λ_А^-1 -1

Пример:

0,3 1,2

А = 0,4 0,1

0.3- λ 1.2

|A- λE|= 0.4 0.1- λ = 0

λ₁=0.9 – число Фробениуса; λ₂= -05

α_А= 10/9 – 1 = 1/9 – запас продуктивности

БИЛЕТ #26

БИЛЕТ #27

БИЛЕТ #28

БИЛЕТ #29

БИЛЕТ #30

БИЛЕТ #31

Вместо параллельности и перпендикулярности используем соответственно слова коллинеарность и ортогональность.

Два вектора плоскости линейно зависимы тогда и только тогда, когда они коллинеарны, верно также обратное. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Коллинеарными называются как сонаправленные, так и противоположно направленные вектора.

Для того чтобы два вектора плоскости   были коллинеарны, необходимо и достаточно, чтобы их соответствующие координаты были пропорциональны  . По существу, это покоординатная детализация очевидного соотношения  .

Пример 1

а) Проверить, коллинеарны ли векторы  . б) Образуют ли базис векторы  ?

Решение:  а) Выясним, существует ли для векторов   коэффициент пропорциональности  , такой, чтобы выполнялись равенства  : , значит, данные векторы коллинеарны.

Обязательно расскажу о «пижонской» разновидности применения данного правила, которая вполне прокатывает на практике. Идея состоит в том, чтобы сразу составить пропорцию   и посмотреть, будет ли она верной:

Составим пропорцию из отношений соответствующих координат векторов:

Сокращаем: , таким образом, соответствующие координаты пропорциональны, следовательно,  

б) Два вектора плоскости образуют базис, если они не коллинеарны (линейно независимы). Исследуем на коллинеарность векторы  . Составим систему:

Из первого уравнения следует, что  , из второго уравнения следует, что  , значит, система несовместна (решений нет). Таким образом, соответствующие координаты векторов не пропорциональны.

Вывод: векторы линейно независимы и образуют базис.

Упрощённая версия решения выглядит так:

Составим пропорцию из соответствующих координат векторов  : , значит, данные векторы линейно независимы и образуют базис.

Обычно такой вариант не бракуют рецензенты, но возникает проблема в тех случаях, когда некоторые координаты равны нулю. Вот так:  . Или так:  . Или так:  . Как тут действовать через пропорцию? (действительно, на ноль же делить нельзя).

Для двух векторов плоскости эквиваленты следующие утверждения: 1) векторы линейно независимы; 2) векторы образуют базис; 3) векторы не коллинеарны; 4) векторы нельзя линейно выразить друг через друга; + 5) определитель, составленный из координат данных векторов, отличен от нуля.

Соответственно, эквивалентны следующие противоположные утверждения: 1) векторы линейно зависимы; 2) векторы не образуют базиса; 3) векторы коллинеарны; 4) векторы можно линейно выразить друг через друга; + 5) определитель, составленный из координат данных векторов, равен нулю.

Рассмотрим более подробно новый, пятый пункт: два вектора плоскости   коллинеарны тогда и только тогда, когда определитель, составленный из координат данных векторов, равен нулю: 

Решим Пример 1 вторым способом:

а) Вычислим определитель, составленный из координат векторов  : , значит, данные векторы коллинеарны.

б) Два вектора плоскости образуют базис, если они не коллинеарны (линейно независимы). Вычислим определитель, составленный из координат векторов  : , значит, векторы   линейно независимы и образуют базис.

Определим коллинеарность векторов пространства.

Правило очень похоже. Для того чтобы два вектора пространства   были коллинеарны, необходимо и достаточно, чтобы их соответствующие координаты были пропорциональны  .

Пример 5

Выяснить, будут ли коллинеарны следующие векторы пространства:

а)  ; б)  в) 

Решение: а) Проверим, существует ли коэффициент пропорциональности для соответствующих координат векторов:

Система не имеет решения, значит, векторы   не коллинеарны.

«Упрощёнка» оформляется проверкой пропорции  . В данном случае:  – соответствующие координаты не пропорциональны, значит, векторы   не коллинеарны.

БИЛЕТ #32

Уравнением линии (или кривой) на плоскости Oxy называется такое уравнение F(x;y)=0 с двумя переменными, которому удовлетворяют координаты x и y каждой точки линии и не удовлетворяют координаты любой точки, лежащей вне этой линии.

Примеры:

1. Уравнение окружности: (x — x_о)² + (y — y_о)² = r²

2. Уравнение прямой с угловым коэффициентом: y = k·x + b

Лежат ли точки K(-2;1) и L(1;1) на линии 2x+y+3?

Решение: Подставив в уравнение вместо x и y координаты точки K, получим 2(-2)+1+3=0. Следовательно, точка K лежит на данной линии. Точка L не лежит на данной линии, так как уравнение 2+1+3=0 не верно.

Уравнением данной поверхности в прямоугольной системе координат Oxyz называется такое уравнение F(x;y;z)=0 с тремя переменными , которому удовлетворяют координаты каждой точки, лежащей на поверхности и не удовлетворяют координаты точек, не лежащих на этой поверхности.

Уравнение сферы

Найдем уравнение сферы радиуса R с центром в точке O₁(x₀;y₀;z₀). Согласно определению сферы расстояние любой ее точки М(х; у; z) от центра O₁(x₀;y₀;z₀) равно радиусу R, т. е. O₁M= R. Но  , где  . Следовательно,

Это и есть искомое уравнение сферы. Ему удовлетворяют координаты лю­бой ее точки и не удовлетворяют координаты точек, не лежащих на данной сфере.

Если центр сферы Ο₁ совпадает с началом координат, то уравнение сферы принимает вид    .

Если же дано уравнение вида F(x;y;z) = 0 , то оно, вообще говоря, определяет в пространстве некоторую поверхность.

Выражение «вообще говоря» означает, что в отдельных случаях уравнение F(x; y; z)=0 может определять не поверхность, а точку, линию или вовсе не определять никакой геометрический образ. Говорят, «поверхность вырождается».

Так, уравнению   не удовлетворяют никакие дей­ствительные значения х, у, z. Уравнению   удовлетворяют лишь координаты точек, лежащих на оси Ох (из уравнения следует: у = 0, z = 0, а х — любое число).

Билет #33 Как составить уравнение плоскости по точке и двум неколлинеарным векторам?

Рассмотрим точку   и два неколлинеарных вектора  .Уравнение плоскости, которая проходит через точку   параллельно векторам  ,выражается формулой:

! Примечание: под выражением «вектор параллелен плоскости» подразумевается, что вектор можно отложить и в самой плоскости. Для наглядности я буду откладывать векторы прямо в плоскости.

Принципиально ситуация выглядит так: 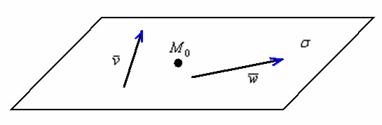Обратите внимание, что точка и два коллинеарных вектора не определят плоскость (векторы будут свободно «вертеться» вокруг точки).

Пример

Составить уравнение плоскости по точке   и векторам  .

Решение: Составим уравнение плоскости по точке и двум неколлинеарным векторам:

Находим определитель

Ответ: 

Как составить уравнение плоскости по трём точкам?

Любые ли три точки пространства задают плоскость? Нет. Во-первых, точки должны быть различными. А во-вторых, они не должны лежать на одной прямой (сразу все три).

Уравнение плоскости, проходящей через три различные точки  , которые не лежат на одной прямой, можно составить по формуле:

На самом деле это разновидность предыдущего способа, смотрим на картинку: 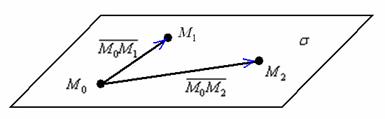Если известны три различные точки, не лежащие на одной прямой, то легко найти два неколлинеарных вектора, параллельных данной плоскости:

Пример

Составить уравнение плоскости по точкам  .

Решение: составим уравнение плоскости по трём точкам. Используем формулу:

Находим определитель

Ответ: 

Вектор нормали плоскости (нормальный вектор)

Вектор нормали плоскости – это вектор, который перпендикулярен данной плоскости. Очевидно, что у любой плоскости бесконечно много нормальных векторов. Но для решения задач нам будет хватать и одного. 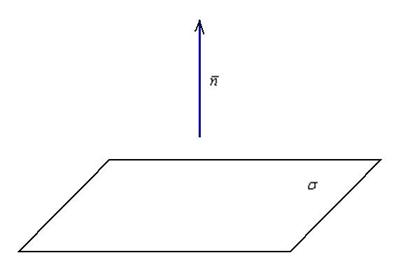Если плоскость задана общим уравнением  , то вектор    является вектором нормали данной плоскости. Просто до безобразия. Всё, что нужно сделать – это «снять» коэффициенты из уравнения плоскости.

Обещанного три экрана ждут, вернёмся к Примеру №1 и выполним его проверку. Напоминаю, что там требовалось построить уравнение плоскости по точке   и двум векторам  . В результате решения мы получили уравнение  . Проверяем:

Во-первых, подставим координаты точки   в полученное уравнение: Получено верное равенство, значит, точка   действительно лежит в данной плоскости.

Во-вторых, из уравнения плоскости снимаем вектор нормали:  . Поскольку векторы   параллельны плоскости, а вектор   перпендикулярен плоскости, то должны иметь место следующие факты:  . Перпендикулярность векторов легко проверить с помощью скалярного произведения:

Вывод: уравнение плоскости найдено правильно.

В ходе проверки я фактически процитировал следующее утверждение теории: вектор   параллелен плоскости   в том и только том случае, когда  .

Пример

Найти единичный нормальный вектор плоскости  .

Решение: Единичный вектор – это вектор, длина которого равна единице. Обозначим данный вектор через  . Совершенно понятно, что векторы   коллинеарны:

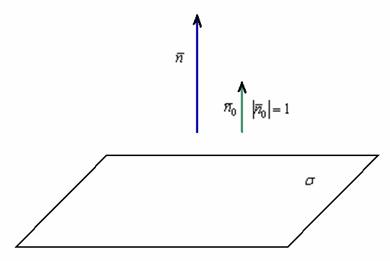
Сначала из уравнения плоскости снимем вектор нормали:  .

Как найти единичный вектор? Для того чтобы найти единичный вектор  , нужно каждую координату вектора   разделить на длину вектора  .

Перепишем вектор нормали в виде   и найдём его длину:

Согласно вышесказанному:

Ответ: