Билет 2

1)Типовая структурная схема 3-х-координатной сау

Возмущающее

воздействие

Суммирующий элемент

(t)

Энергетический канал

y(t)

u

x(t)

Регулятор

Управляемый объект

Рассогла-сование

Входное воздействие

Выходная функция

Управляющее воздействие

y₁(t)

Канал управления

Устройство обратной связи

Контролируемая функция (функция регулируемого параметра)

Элемент главной обратной связи, выполняющий функции масштабирования или преобразования

Виды возмущений

1. Внешние возмущения изменение напряжения питания, изменение нагрузки, трение в передаче между двигателем и объектом, неуравновешенность вращающихся масс и т.п.;

2. Внутренние возмущения изменение характеристик звеньев системы, изменение теплопроводности, дрейф нулей усилителей и т. д.

2. Методика анализа устойчивости сау.

1) определяем полюсы передаточной функции разомкнутой системы;

2) располагаем полюсы на комплексной плоскости;

3) строим АФХ разомкнутой системы;

4) применяем одну из следующих формулировок критерия устойчивости Найквиста.

П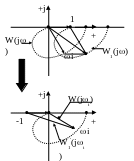 усть введем вспомогательную функцию заменим pj, тогда

Согласно принципа аргумента изменение аргумента D(j) и D_з(j) при 0<< равно Тогда то есть годограф W₁(j) не должен охватывать начало координат.

Для упрощения анализа и расчетов сместим начало радиуса-вектора из начала координат в точку (-1, j0), а вместо вспомогательной функции W₁(j) используем АФХ разомкнутой системы W(j).