5. Отчет должен содержать:

1. Схемы измерения.

2. Таблицы использованного оборудования и приборов с их паспортными данными.

3. Основные расчетные формулы.

4. Таблицы опытных и расчетных данных.

5. Графики и диаграммы.

6. Выводы по работе.

6. Вопросы.

   1. В какой цепи и при каких условиях возникает резонанс?

   2. Как различают резонанс напряжений и резонанс токов?

   3. Что такое волновое сопротивление и добротность контура Q?

   4. Как экспериментально можно определить Q и .

   5. Как влияет величина Q на резонансные свойства контура?

   6. Как определяют полосу пропускания контура?

Литература

1. Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. Т.1, ч.II, 6-1; 6-3. М., Энергия, 1966.

Лабораторная работа № 10. Исследование свободных процессов в электрических цепях

1. Цель работы.

Изучение влияния параметров цепи и числа накопителей энергии на вид переходного процесса. Исследование возможностей экспериментальной оценки основных характеристик свободных процессов.

2. Содержание работы.

Исследование переходного процесса в цепях с одним, двумя или тремя накопителями энергии. Определение постоянной времени цепи и декремента затухания по осциллограммам переходного процесса.

3. Основные теоретические положения.

   1. Переходным процессом называется процесс перехода от одного установившегося режима к другому. Переходный процесс возникает при всяком изменении топологии цепи или изменения внешнего воздействия (источника). Такое изменение в общем случае называется коммутацией цепи. За начало переходного процесса (момент коммутации) принимают момент времени , причем через обозначают, момент времени, непосредственно предшествующий коммутации (последний момент перед коммутацией), а через или просто момент времени, следующий непосредственно за коммутацией (первый момент после коммутации).

Переход реальной электрической цепи от одного установившегося режима к другому не может происходить мгновенно, скачком. Это объясняется тем, что каждому установившемуся состоянию соответствует определенное значение энергии, запасенной в электрическом и магнитном полях . Мгновенный переход от одного установившегося режима к другому потребовал бы скачкообразного изменения запасенной энергии, что возможно только при наличии источника энергии бесконечно большой мощности. В связи с тем, что любой реальный источник энергии может отдавать только конечную мощность, суммарная энергия, запасенная в цепи, может изменяться только плавно, не имея скачков. Отсюда следует, что и . Отсюда также можно получить соотношения и , и . Последние соотношения называются законами коммутации. Таким образом, переходные процессы могут возникать только в цепях, содержащих накопители энергии – индуктивности и емкости.

Если переходные процессы происходят только за счет внутренних запасов энергии электрического и магнитного полей, без участия внешних источников, то такие процессы называют свободными. Они описываются уравнением вида

, (1)

решение, которого при простых корнях имеет вид

. (2)

2. Свободные процессы при одном накопителе энергии. Рассмотрим цепь с емкостью

Уравнение цепи

(3)

и решение его

, (4)

где - начальное значение напряжения на емкости;

- показатель затухания процесса (корень соответствующего характеристического уравнения).

Величина называется постоянной времени цепи и обозначается буквой , и следовательно для цепи . Тогда из (4) видно, что при , напряжение изменяется в раз. График изменения напряжения на емкости, построенный по уравнению (4), называется экспонентой.

Постоянную времени можно найти из графика рис.2. Действительно

. (5)

Поделив первое на второе и логарифмируя полученное выражение получим:

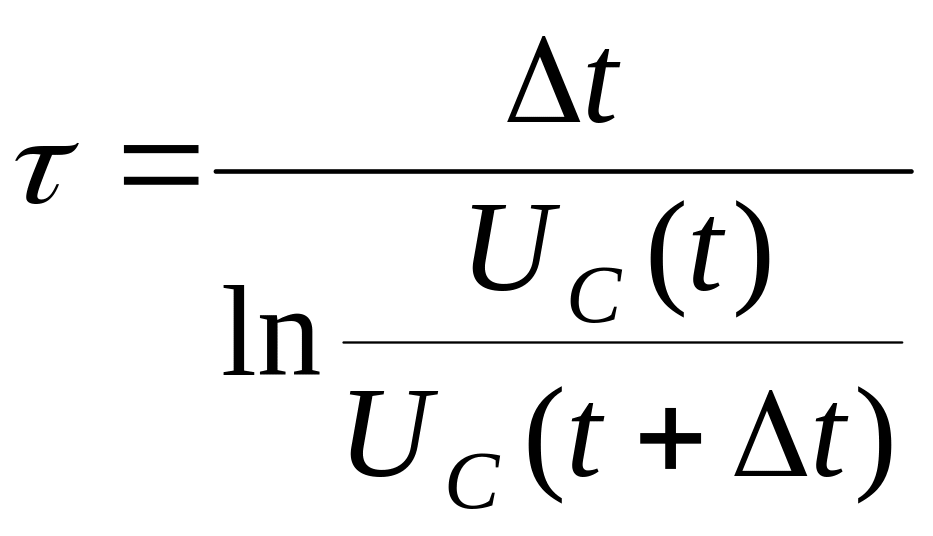. (6)

Для тока в цепи R, С имеем:

. (7)

Ток отрицателен по отношению к напряжению на емкости, что указывает на процесс разряда конденсатора.

Из (4) и (7) следует, что теоретически переходный процесс закончится при . Для большинства инженерных расчетов считают переходный процесс закончившимся, если значение тока или напряжения в переходном режиме отличается менее чем на 5% от установившегося значения. Из схемы рис.1 следует, что установившееся значение равно нулю (конденсатор полностью разряжен). Итак, мы должны считать переходный процесс закончившимся, если .

При имеем:

, (8)

откуда

,

т.е. при переходный процесс закончился. Для инженерных расчетов время переходного процесса принимают равным:

. (9)

Для цепи с индуктивностью

уравнение свободного процесса

(10)

и решение его

, (11)

где - начальное значение тока в индуктивности, - показатель затухания переходного процесса.

Величина называется постоянной времени цепи .

График тока в индуктивности будет иметь вид

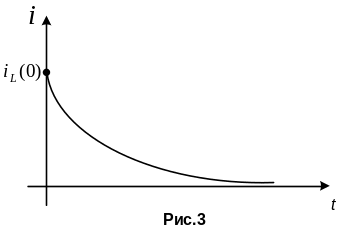
3. Свободные процессы при двух накопителях энергии.

Рассмотрим схему рис.4.

Уравнение, описывающее процессы в цепи рис.4 имеет вид:

(12)

или

, (13)

где - начальное значение напряжения на конденсаторе. Перепишем (13) в виде:

(14)

и отметим, что уравнение (14) второго порядка, а значит, решение содержит 2 слагаемых:

, (15)

где - постоянные интегрирования,

- корни характеристического уравнения.

Переписав (14) в виде:

(16)

и введя обозначения ; получим уравнение свободного процесса при двух накопителях энергии

, (17)

характеристическое уравнение: ,

корни которого имеют вид:

. (18)

3.3.1. Свободные процессы при условии , то есть

.

В этом случае имеем корни вещественные и разные

,

а решение для тока и напряжения при из (15) будет иметь вид:

. (19)

Такой процесс разряда конденсатора называется апериодическим, и свободный процесс также апериодическим.

где момент времени, при котором наступает максимум тока.

3.3.2. Свободные процессы при условии , т.е.

.

В этом случае корни будут комплексно сопряженными:

,

где

.

Решения для тока и напряжения при из (15) будет иметь вид:

,

. (20)

Такой процесс носит название колебательного.

Можно отметить особенности кривых и . Максимум тока и ноль напряжения на емкости сдвинуты относительно момента времени . Момент времени максимума тока и равен:

.

Момент времени нуля напряжения на емкости и равен

.

При чисто гармонических колебаниях и совпадают с .

Как следует из (20), амплитуда тока и напряжения с течением времени затухает. Быстроту затухания принято характеризовать отношением двух последующих амплитуд одного знака, который называется декрементом затухания (колебаний):

. (21)

Для оценки затухания применяются и логарифмический декремент затухания:

. (22)

Оценить переходный процесс можно и по значению корней характеристического уравнения:

.

Огибающая затухающих колебаний определяется кривой . Чем больше (вещественная часть корня), тем быстрее затухает колебательный процесс. При переходный процесс можно считать закончившимся. Мнимая часть корня определяет частоту или период свободных (затухающих) колебаний.

.

3.3.3. Свободные процессы при условии , т.е.

.

В этом случае корни будут вещественными и равными.

Решение для тока и напряжения запишется в виде:

. (23)

Свободный процесс остается апериодическим, но это критический (предельный) случай.

4. Свободные процессы при 3-х накопителях энергии.

В этом случае дифференциальное уравнение, описывающее процессы в цепи будет 3-го порядка и решение его примет вид:

. (24)

В зависимости от топологии цепи и величин параметров корни характеристического уравнения могут принимать различные значения.

Например, для схемы рис.7:

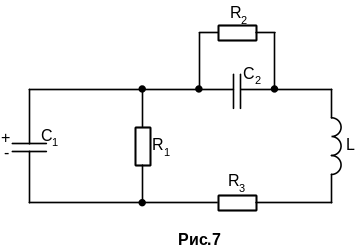
при условии и корни определяются выражениями: ; ,

где

.

И тогда график свободного процесса принимает сложный вид: на некоторую экспоненту накладывается колебательный процесс с затухающей амплитудой.