2.3 Риск-анализ в диапазоне времени

Для нахождения значений ущерба при заданном уровне риска необходимо решить следующее уравнение[79]:

где – пиковое значение риска,

– коэффициент , задающий уровень отсчета от

(2.45)

Для поиска решения уравнения, прологарифмируем его:

(2.46)

Для упрощения записи введем обозначение:

(2.47)

Получим уравнение:

(2.48)

или

(2.49)

(2.50)

Для нахождения корней уравнения нужно воспользоваться разложением в ряд Тейлора. Ряд Тейлора – разложение функции в бесконечную сумму степенных функций. Ряды Тейлора применяются при аппроксимации функции многочленами. Функция бесконечно дифференцируема в некоторой окрестности точки. Ряд Тейлора для этой функции будет иметь вид:

где – производная -ой степени,

– точка в окрестности, которой производится разложение.

Разложим натуральные логарифмы , и в ряд Тейлора в окрестности точки . При разложении ограничимся пятью первыми членами ряда, при этом погрешность будет незначительной. Очевидно, что при дальнейшем разложении получим уравнение пятой степени, которое, согласно теореме Руффини–Абеля, в общем случае не имеет аналитического решения в радикалах. Для упрощения записи определим необходимые производные для дальнейшего расчета.

Производные равны:

(2.52)

В свою очередь производные будут равны:

(2.53)

Для производные равны:

(2.54)

.

После эквивалентных преобразований уравнение примет вид:

(2.55)

Используя формулы сокращенного умножения

перезапишем последнее уравнение

в следующем виде

(2.56)

Для упрощения вычислений введем обозначения:

(2.57)

(2.58)

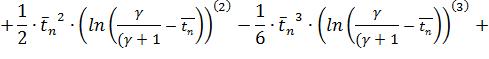
(2.59)

Используя полученные обозначения, перепишем уравнение:

(2.60)

В результате имеем уравнение четвертой степени, которое разрешимо в радикалах. Таким образом можно найти границы временного интервала при заданном уровне риска.

2.4 Оценка общего риска многокомпонентной системы на основе параметров рисков её атакуемых компонентов

После того, как осуществлена оценка рисков компонентов РАИС, был определен закон распределения и найдены параметры риска для каждого компонента, представляется возможным оценить риск системы в целом. При этом нужно исходить из того, что в РАИС ущербы, возникающие при гибели ее компонент слабо коррелированны между собой. Общий ожидаемый ущерб системы в таком случае можно найти как сумму ущербов в отдельных ее компонентах. Данное допущение справедливо как для детерминированных, так и для случайных величин. Следовательно, относительная независимость этих параметров дает возможность осуществления соответствующих вероятностных оценок.

Выражение для оценки риска в этом случае для реализации синхронной и асинхронной атаки соответственно принимает вид[68,70]:

где: – значение ущерба при «смерти»i-ой компоненты;

– плотность вероятности наступления ущерба в момент времени ;

– количество компонент системы, подвергшейся атаке.

В случае распределения времени «гибели» системы по логлогистическому закону имеем:

(2.63)

(2.64)

где: – параметры логлогистического распределения для i-ой компоненты.

Для полученных выражений остается открытым вопрос о том, какие значения следует принимать во внимание. Возможны два варианта: пиковая и средняя оценка.

При пиковой оценке используются координаты максимума риска и общее выражение будет выглядеть следующим образом:

где – значение максимума риска в i-ой компоненте системы;

– время «гибели» системы, при котором достигается пик риска в i-ой компоненте системы.

Для логлогистического распределения получаем:

(2.67)

(2.68)

При использовании усредненных оценок в компонентах общий риск системы можно рассчитать с помощью выражения:

Для логлогистического распределения имеет место следующее выражение:

(2.71)

(2.72)

Полученные выше выражения позволяют оценивать риск для случая совместного и несовместного воздействия сетевых атак.

В настоящей главе также получена аналитическая зависимость ущерба от времени для заданной функции полезности. Было найдено аналитическое выражение риска фатального отказа атакуемого компонента системы, отражающая не только возможность появления неблагоприятного события, но и последствия наступления данного события – ущерб и для эффективной оценки риска было осуществлено исследование его параметров и найдены их аналитические выражения.