МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
МЕЖДУНАРОДНЫЙ ИНСТИТУТ ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ
КАФЕДРА «ИНФОРМАНЦИОННЫЕ СИСТЕМЫ И ТЕХНОЛОГИИ»
Методические указания к контрольной работе
«Моделирование систем массового обслуживания в среде mathcad»
для специальностей
53 01 02 Автоматизированные системы обработки информации,
40 01 01 Программное обеспечение информационных технологий,
40 01 02 Информационные системы и технологии.
Минск 2009 г.
Настоящий материал предназначен для использования в качестве методических указаний при выполнении контрольных работ студентами, получающими образование на основе дистанционной формы обучения по дисциплине: «Математическое моделирование информационных процессов».
Материалы данного пособия могут быть использованы при проведении лабораторных занятий по курсу «Прикладная математика» для студентов специальности 40 01 01 «Программное обеспечение информационных технологий», 40 01 02 «Информационные системы и технологии», и по курсу «Компьютерные методы инженерного моделирования на основе CAS», для студентов специальности для специальности 40 01 02 «Информационные системы и технологии (по направлениям)» направление 40 01 02-01 «Информационные системы и технологии в проектировании и производстве»
Целью данной работы является приобретение студентами навыка работы в среде MATHCAD по созданию моделей систем массового обслуживания.
Составители:
к.т.н, доцент В.В. Напрасников, преподаватель Ю.В. Напрасникова, доцент В. И. Лакин, преподаватель Ю. И. Монич (Белорусский Национальный технический университет)
1. Простейшие потоки событий 4
2. Замкнутые системы массового обслуживания 6
3. Открытые системы массового обслуживания 7
4. Создание программных модулей и элементы программирования в среде MathCAD. 10
5. Средства системы MATHCAD для моделирования на основе обыкновенных дифференциальных уравнений 18
Задание 1. Стационарный режим, открытая СМО. 23
Пример решения в среде MathCAD. Открытая СМО с очередью 23
23
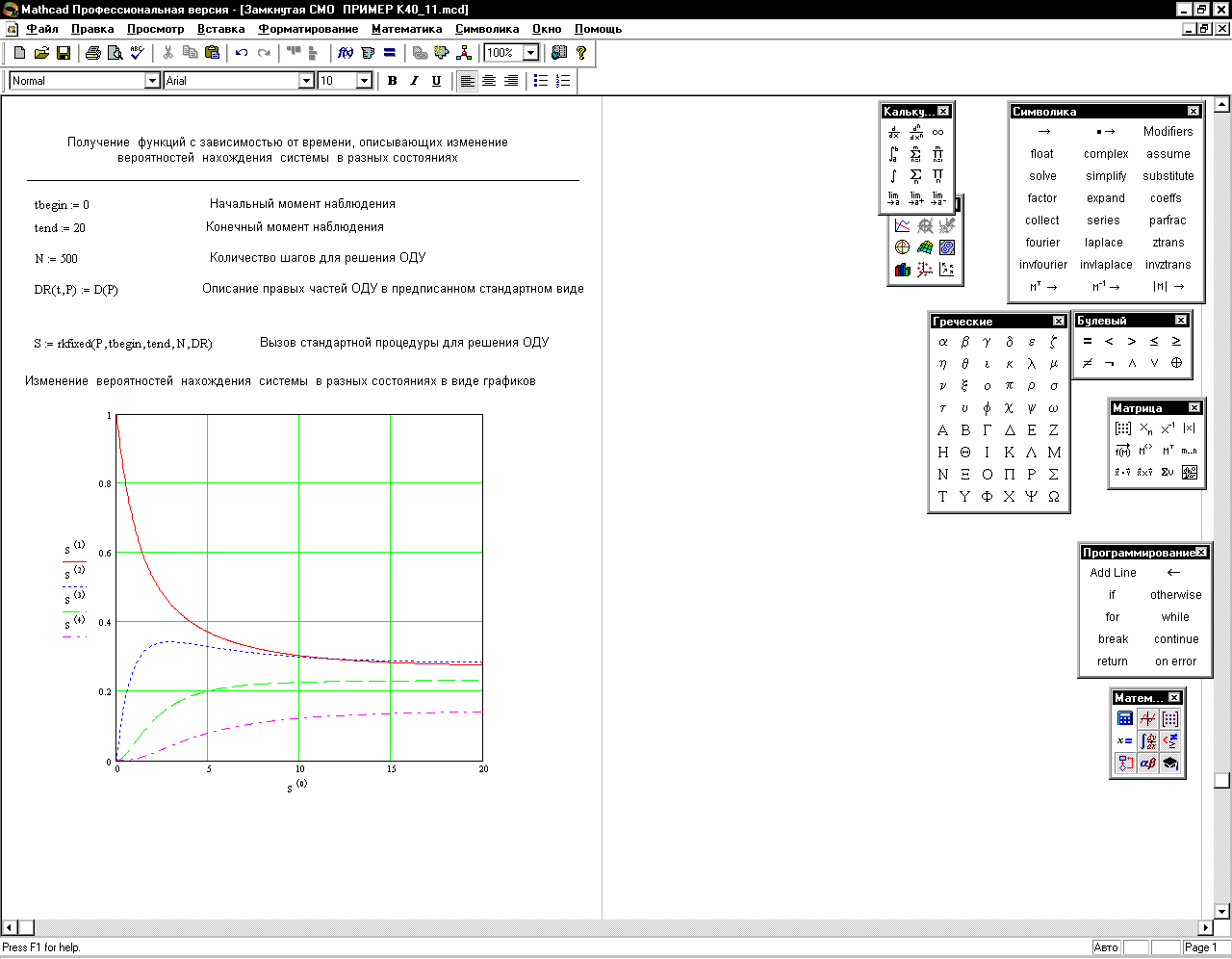
Задание 2. Нестационарный режим, замкнутая СМО с очередью 27
Пример решения в среде MathCAD. Нестационарный режим, замкнутая СМО с очередью 28
Литература. 31
1. Простейшие потоки событий
Потоком событий называется последовательность однородных событий, следующих одно за другим в случайные моменты времени. Такой поток можно изобразить как последовательность точек t1...tn на числовой оси, соответствующих случайным моментам появления событий (рис.1.):
Рис.1. Последовательность однородных событий
Поток событий называется стационарным, если вероятность попадания того или иного числа событий на участок времени зависит только от длины этого участка и не зависит от того, где именно на оси 0t расположен этот участок.
Поток событий называется потоком без последействия, если для любых непересекающихся участков времени число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой. Поток событий называется ординарным, если вероятности попадания на участок времени малой длины двух или более событий пренебрежимо малы по сравнению с вероятностью попадания на этот участок одного события.
Стационарность потока означает, что вероятностные характеристики этого потока не должны меняться в зависимости от времени. Например, такая характеристика, как интенсивность потока событий, равная математическому ожиданию числа событий в единицу времени, должна оставаться постоянной для стационарного потока.
На практике часто встречаются потоки событий, которые стационарны только на ограниченном участке времени. Например, поток вызовов, поступающих на телефонную станцию в дневное время, может считаться таковым. Тот же поток в течение целых суток уже не будет стационарным, поскольку ночью интенсивность вызовов гораздо меньше, чем днем.
Отсутствие последействия в потоке означает, что события появляются в последовательные моменты времени независимо друг от друга. Например, поток пассажиров, входящих на станцию метро, можно считать потоком без последействия потому, что причины, обусловившие приход отдельного пассажира именно в тот, а не другой момент, не связаны с аналогичными причинами для других пассажиров. Однако условие отсутствия последействия может быть нарушено за счет появления такой зависимости. Например, поток пассажиров, покидающих станцию метро, уже не может считаться потоком без последействия, так как моменты выхода пассажиров, прибывших одним и тем же поездом, зависимы между собой.
Ординарность потока означает, что события в потоке приходят поодиночке, а не парами, тройками и т. д. Например, поток клиентов, направляющихся в парикмахерскую, практически можно считать ординарным, чего нельзя сказать о потоке клиентов, идущих в ЗАГС для регистрации брака.
Простейший поток играет среди потоков событий особую роль, до некоторой степени аналогичную роли нормального закона среди других законов распределения. Согласно центральной предельной теореме, при суммировании большого числа независимых случайных величин, подчиненных практически любым законам распределения, получается случайная величина, приближенно распределенная по нормальному закону. Аналогично можно сказать, что при суммировании (взаимном наложении) большого числа ординарных, стационарных потоков с практически любым последействием получается поток, сколь угодно близкий к простейшему. Условия, которые должны для этого соблюдаться, аналогичны условиям центральной предельной теоремы, а именно: складываемые потоки должны оказывать на сумму приблизительно равномерно малое влияние.