19. Свойства целых чисел

Мы предполагаем, что   — система целых чисел. Из аксиом   следует, что при выполнении операций в системе N натуральных чисел и в системе Z целых чисел над натуральными числами можно не пользоваться разными знаками для обозначения операций сложения и умножения. Легко показать, что и вычитание натуральных чисел в обоих случаях, если выполнимо в N, приводит к одному результату. Поэтому мы пользуемся в дальнейшем одним знаком — для обозначения вычитания натуральных чисел, независимо от того, в каком множестве рассматривается это отношение.

Теорема 6.2.1. Всякое целое число есть разность натуральных

Доказательство. Обозначим через М подмножество Z всех таких целых чисел, которые представимы в виде разности натуральных чисел. Имеем:

Поэтому (упражнение 2.5.1)

есть разность натуральных чисел и, следовательно, принадлежит М. В силу аксиомы 

Теорема 6.2.2. Кольцо   коммутативно и с единицей.

Доказательство. Имеем:

Теорема 6.2.3. Каждое целое число — нуль, натуральное или противоположно натуральному.

Доказательство. Теорема 6.2.1.

Теорема 6.2.4. Кольцо целыхчисел можнолинейно и строго упорядочить и притом единственным способом.

Порядок в кольце целых чисел архимедов и продолжает порядок в полукольце натуральных чисел.

Доказательство. Обозначим через   множество N. Из теоремы 6.2.3 и алгебраичности операций на N следует» что   — положительная часть кольца  . Поэтому кольцо   можно линейно упорядочить. Пусть   — какая-нибудь положительная часть этого кольца. Имеем по теореме 5.4.4

Далее, если  , то  . Поэтому

В силу теоремы 5.4.12

Мы имеем дальше

Поэтому порядок в Z продолжает порядок в N. Заметим, наконец, что положительными в кольце целых чисел являются только натуральные числа — элементы   а отсюда следует (вопрос 4.6.7), что порядок в кольце целых чисел архимедов.

Вопросы: 6.2.1. Доказать, что кольцо целых чисел дискретно и даже

6.2.2. Доказать, что уравнение   неразрешимо в 

6.2.3. Доказать, что уравнение   имеет только нулевое (0,0) решение в 

6.2.4 (теорема о делении с остатком). Доказать, что для любого целого числа та и любого натурального числа b можно найти и только одну пару целых чисел   такую, что 

6.2.5. Доказать, что множества Z и N равномощны.

6.2.6. Перечислить аксиомы, которые используются в доказательстве теоремы 6.2.1.

6.2.7. Доказать, что аксиомы   можно вывести из остальных аксиом теории целых чисел.

6.2.8. Показать, что мультипликативную полугруппу целых чисел линейно и строго упорядочить нельзя.

6.2.9. Показать, что существует только один линейный и строгий порядок в аддитивной группе целых чисел, в котором 1 — положительный элемент.

6.2.10. Показать, что:

а) линейный порядок   кольце целых чисел   однозначно определяется следующими условиями:

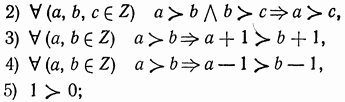
б) ни одно из четырех названных выше условий не является следствием остальных.

6.2.11. Пусть   — группа. Доказать, что

Целое кратное любого элемента а группы   определяется следующими соглашениями:

6.2.12. Пусть   — группа. Доказать, что:

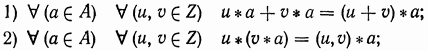
3) если группа А коммутативна, то

6.2.13. Пусть   — группа. Дать определение целой степени любого элемента группы А и сформулировать свойства целой степени, аналогичные указанным в вопросе 6.2.12.

6.2.14. Пусть   — архимедовски линейно и строго упорядоченное поле. Доказать, что для любого элемента а поля Р существует и только одно целое число а такое, что

Число а с указанным в вопросе 6.2.14 свойством называют целой частью элемента и обозначают символом 

18. Операции над целыми числами

Конец формы

В компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком: прямой код, обратный код, дополнительный код. Последние две формы применяются особенно широко, так как позволяют упростить конструкцию арифметико-логического устройства компьютера путем замены разнообразных арифметических операций операцией сложения.

Положительные числа в прямом, обратном и дополнительном коде изображаются одинаково – двоичными кодами с цифрой 0 в знаковом разряде.

Пример, число 12

Прямой код	0	0	0	0	1	1	0	0
Обратный код	0	0	0	0	1	1	0	0
Дополнительный код	0	0	0	0	1	1	0	0

Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение.

Прямой код. В знаковый разряд помещается цифра 1, а в разряды цифровой части числа – двоичный код его абсолютной величины.

Обратный код получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы –  нулями.

Дополнительный код получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду.

Пример, число -12

Прямой код	1	0	0	0	1	1	0	0
Обратный код	1	1	1	1	0	0	1	1
Дополнительный код	1	1	1	1	0	1	0	0

Обычно отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный или дополнительный двоичный код и в таком виде хранятся, перемещаются и участвуют в операциях. При выводе таких чисел из машины происходит обратное преобразование в отрицательные десятичные числа.

17. Отрицательные числа появились значительно позже натуральных чисел и обыкновенных дробей. Первые сведения об отрицательных числах встречаются у китайских математиков во II в. до н. э. Положительные числа тогда толковались как имущество, а отрицательные – как долг, недостача. Но ни египтяне, ни вавилоняне, ни древние греки отрицательных чисел не знали. Лишь в VII в. индийские математики начали широко использовать отрицательные числа, но относились к ним с некоторым недоверием. В Европе отрицательными числами начали пользоваться с XII–XIII вв. , но до XVI в. , как и в древности, они понимались как долги, большинство ученых считали их “ложными”, в отличие от положительных чисел – “истинных”. Признанию отрицательных чисел способствовали работы французского математика, физика и философа Ренё Декарта. Он предложил геометрическое истолкование положительных и отрицательных чисел – ввел координатную прямую. Складывать и вычитать отрицательные числа научились древнекитайские ученые еще до нашей эры. Индийские математики представляли себе положительные числа как, “имущества”, а отрицательные числа как “долги”. Вот как индийский математик Брахмагупта излагал правила сложения и вычитания: “Сумма двух имуществ есть имущество”, “сумма двух долгов есть долг”, “сумма имущества и долга равна их разности” и т. д.

16. Расширение понятия числа

I. Множество натуральных чисел – это множество чисел, которыми пользуются при счете предметов.

.

Всякому натуральному числу соответствует точка на числовой прямой.

Задание: Назовите самое маленькое натуральное число. Существует ли самое большое натуральное число?

II. Множество целых чисел – это множество, состоящее из натуральных чисел, им противоположных чисел и нуля.

.

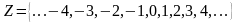Всякому целому числу соответствует точка на числовой прямой.

Задания:

Существуют ли самое маленькое и самое большое целое число?

Верно ли утверждение:

любое натуральное число является целым;

любое целое число является натуральным?

III. Множество рациональных чисел – это множество несократимых дробей вида

.

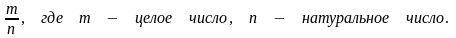
Всякому рациональному числу соответствует точка на числовой прямой.

Свойство рациональных чисел: Всякое рациональное число можно представить в виде бесконечной периодической десятичной дроби.

Обратно: всякая бесконечная периодическая десятичная дробь является рациональным числом.

15. Окружностью называется линия, все точки которой равноудалены от заданной. Расстояние от центра до любой точки окружности называется радиусом. Расстояние между двумя точками (а мы берём расстояние от центра до любой точки окружности) вычисляется по формуле d^2=(x-x0)^2+(y-y0)^2, где х0 и у0 - координаты первой точки,(в частности центра окружности) х,у - координаты второй точки (в частности любой точки окружности) и так как радиус число постоянное, то получаем r^2=(x-x0)^2+(y-y0)^2, где х0 и у0 - координаты центра окружности, х,у - координаты любой точки окружности. Или r=квадратный корень из (x-x0)^2+(y-y0)^2, кстати во многих ответах ошибки, уравнение х^2+y^2=R^2 частный случай обще Выведем уравнение вида X^2+Y^2=R^2: 1. Рисуем окружность в центре системы координат радиуса R 2. Выбираем произвольную точку на окружности и рисуем проекции точки на оси ОX и OY, также проводим отрезок от центра окружности к нашей точке (он равен R) 3. В получившемся прямоугольнике рассмотри любой из треугольников. По т. Пифагора: Lx^2+Ly^2=R^, где Lx - длина проекции на OX, .. 4. Для совокупности точек лежащей на нашей окружности будем менять Lx и Ly, обозначим их как новые переменные Lx=X и Ly=Y и получаем X^2+Y^2=R^2. Таким образом меняя произвольно X и Y, мы будем получать точки окружности радиуса R. го уравнения окружности,

14. Теорема.

Всякое уравнение первой степени вида  , где А, В и С – некоторые действительные числа, причем А и В одновременно не равны нулю, задает прямую линию в прямоугольной системе координат Oxy на плоскости, и любая прямая в прямоугольной системе координат Oxy на плоскости задается уравнением вида   при некотором наборе значений A, B и C.

Доказательство.

Как видите, теорема состоит из двух частей. Докажем сначала, что уравнение вида   задает прямую на плоскости.

Пусть координаты точки   удовлетворяют уравнению  , то есть,  . Вычтем из левой и правой частей уравнения  соответственно левую и правую части равенства  , при этом получаем уравнение вида  , которое эквивалентно  .

Уравнение   представляет собой необходимое и достаточное условие перпендикулярности двух векторов   и  . То есть, множество всех точек   определяет в прямоугольной системе координат Oxy прямую линию, перпендикулярную направлению вектора  . Если бы это было не так, то векторы   и   не были бы перпендикулярными и равенство   не выполнялось бы.

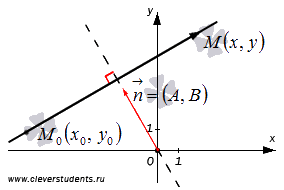
Таким образом, уравнение   задает прямую линию в прямоугольной декартовой системе координат Oxy на плоскости, следовательно, эквивалентное ему уравнение вида   задает эту же прямую. На этом первая часть теоремы доказана.

Теперь докажем, что всякая прямая в прямоугольной системе координат Oxy на плоскости определяется уравнением первой степени вида  .

Пусть в прямоугольной системе координат Oxy на плоскости задана прямая a, проходящая через точку  ,   - нормальный вектор прямой a, и пусть   - плавающая точка этой прямой. Тогда векторы   и   перпендикулярны, следовательно, их скалярное произведениеравно нулю, то есть,  . Полученное равенство можно переписать в виде  . Если принять  , то получим уравнение  , которое соответствует прямой a.

На этом доказательство теоремы завершено.

Уравнение вида   есть общее уравнение прямой на плоскости в прямоугольной системе координат Oxy.

Из доказанной теоремы следует, что в фиксированной прямоугольной декартовой системе координат Oxy на плоскости прямая линия и ее общее уравнение прямой неразделимы. Иными словами, заданной прямой соответствует ее общее уравнение прямой, а этому общему уравнению прямой соответствует заданная прямая.

Из доказательства теоремы также видно, что коэффициенты А и В при переменных x и yявляются соответствующими координатами нормального вектора прямой, заданной общим уравнением прямой вида  .

Приведем пример общего уравнения прямой.

Уравнению   соответствует прямая линия в заданной прямоугольной декартовой системе координат Oxy. Ее изображение представлено на чертеже. Нормальным вектором этой прямой линии является вектор  .

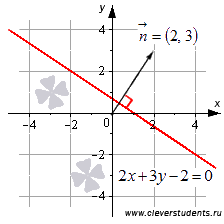
С другой стороны, прямая линия, изображенная на рисунке, в прямоугольной системе координат Oxy задается общим уравнением прямой вида  , так как координаты любой точки этой прямой удовлетворяют записанному уравнению.

Следует заметить, что уравнение вида  , полученное из общего уравнения прямой умножением его обеих частей на отличное от нуля число  , эквивалентно уравнению  , следовательно, определяет ту же самую прямую на плоскости в фиксированной прямоугольной системе координат.