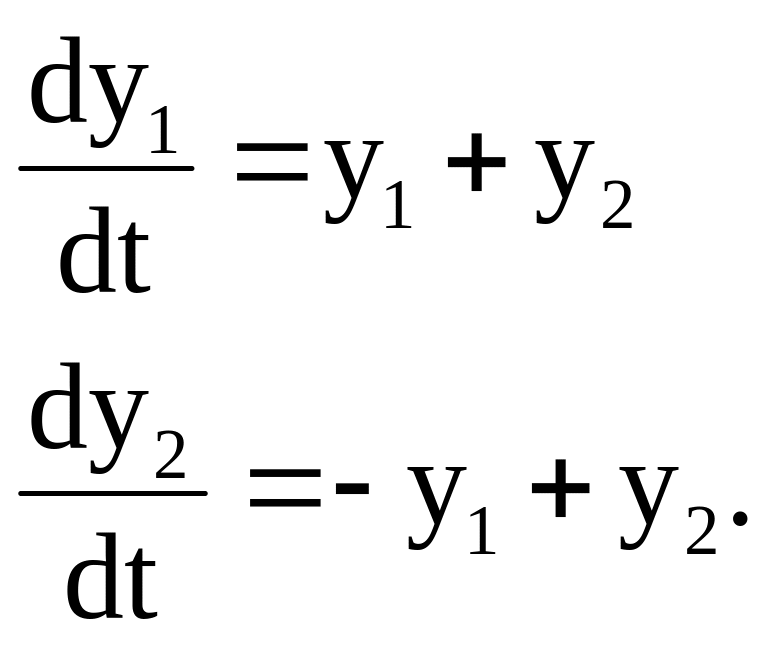Глава 9. Устойчивость нелинейных систем

§1. Устойчивость по Ляпунову

Общая теория устойчивости нелинейных систем была развита в работах А.М. Ляпунова.

При исследовании устойчивости нелинейных систем рассматривает­ся устойчивость отдельных видов движения (устойчивость состоя­ний равновесия, устойчивость автоколебаний).

Определение устойчивости по Ляпунову в применении к состоя­нию равновесия формулируется следующим образом:

состояние равновесия является устойчивым, если для любой заданной области допустимых отклонений от состояния равновессия (область ε, рис. 108) можно указать такую область начальных условий (ε), окружающую состояние равновесия, что ни одно движение, начинающееся внутри (ε), никогда не достигнет границы ε. Состояние равновесия на­зывается неустойчивым, если может быть указана такая область отклонений от состояния равновесия (область ε), для кото­рой не существует области (ε), окружающей состояние равно­весия и обладающей тем свойством, что ни одно движение, на­чинающиеся внутри (ε), никогда не достигнет границы облас­ти ε.

Условия устойчивости, сформулированные выше, могут быть запи­саны следующим образом.

Состояние равновесия y₁=0, y₂=0 устойчиво, если для любого заданного ε>0 имеется (ε) такое, что если при t=0:

|y1(0)|<	и	|y2(0)|<
то для 0<t<
|y1(t)|<ε	и	|y2(t)|<ε.

На фазовой плоскости этому определению соответствует квадрат ε, внутри которого находится начальная точка фазовой траектории. Требование устойчивости означает, что фазовые траектории не дол­жны выходить из этого квадрата.

Рис. 108

Поясним определение устойчивости по Ляпунову.

Если мы задаем область допустимых отклонений Е, то от нее зависит область допустимых начальных условий . Кроме того в соответствии с этим определением для устойчивой систе­мы не требуется, чтобы она обязательно возвращалась к прежнему состоянию равновесия (т. 0 на рис. 108), а достаточно, чтобы движение изображающей точки происходило внутри допустимой об­ласти отклонений ε. Если же система не только не выходит за границы допустимой области, но и возвращается к прежнему состоянию равновесия, то такая система называется асимптотически устойчивой. Устойчивость состояния равновесия по Ляпунову гарантирует устойчивость в малом. Однако такая система может оказаться неустойчивой в большом (рис. 109).

Рис. 109

Для исследования устойчивости нелинейных систем Ляпуновым предложено два метода. Первый из них позволяет исследовать ус­тойчивость системы "в малом", а второй "в большом".

§2. Первый метод Ляпунова

Пусть исходная нелинейная система задана в виде двух дифференциальных нелинейных уравнений первого порядка:

Необходимо исследовать устойчивость состояния равновесия с координатами Y₁₀, Y₂₀. Очевидно, что в состоянии равнове­сия

,

т.е. точка с координатами y₁₀, y₂₀ является одной из точек пересечения кривых P(Y₁,Y₂)=0 и Q(Y₁,Y₂)=0. Так как нашей задачей является исследование устойчивости состояния равновесия (Y₁₀, Y₂₀), то это значит, что нас интересует характер движения вблизи от этого состояния равновесия. Введем новые переменные, (вместо Y₁, Y₂), которые характеризуют отклонение от состояния равновесия – y₁ и y₂. Если Р(Y₁,Y₂)=0 и Q(Y₁,Y₂)=0 являются аналитическими функциями, то их можно разложить в ряд Тейлора. Имеем:

	(9-1а)
	(9-1б)

где y₁=Y₁-Y₁₀; y₂=Y₂-Y₂₀

R₁ и R₂ – объединяют все члены степени выше первой относительно y₁ и y₂.

Первый метод исследования устойчивости, предложенный Ляпу­новым, заключается в следующем. Отбросим в выражении (9-1а) и (9-1б) нелинейные члены и перейдем к уравнениям в отклоне­ниях от состояния равновесия. Получим:

(9-2)

Эта система уравнений носит название уравнений первого приближения. Исследование устойчивости этой системы уравнений за­труднений не представляет, так как мы имеем линейную систему с постоянными коэффициентами. Характеристическое уравнение сис­темы имеет вид:

p2-(a+d)p+ad-bc=0

(9-3)

Характер устойчивости решения определяется корнями Р₁ и Р₂ характеристического уравнения (9-3). Если эти корни находят­ся в левой полуплоскости комплексного переменного (см. главу 3), то система первого приближения устойчива.

Ляпунов доказал следующие теоремы:

1. Если линейная система первого приближения устойчива, то соответствующее состояние равновесия исходной нелинейной системы будет устойчиво.

2. Если линейная система первого приближения неустойчива, то соответствующее остояние равновесия исходной нелинейной системы также неустойчиво.

3. Если линейная система первого приближения находится на границе устойчивости, то судить об устойчивости исходной нели­нейной системы по уравнениям первого приближения нельзя и необ­ходимо рассматривать исходную нелинейную систему.

Пользуясь этими теоремами, можно по результатам исследования уравнений первого приближения судить об устойчивости "в малом" состояния равновесия исходной нелинейной системы.

Пример. Исходная нелинейная система описывается уравнениями:

Найдем состояния равновесия этой системы из условия, что в рав­новесном состоянии P(Y₁,Y₂)=Q(Y₁,Y₂)=0:

Y10=Y20=1	Два состояния равновессия – А(1,1) и В(-1,-1).
Y10=Y20=-1

Запишем линеаризованные уравнения для точки А:

a=1; c=-1 b=1; d=1

Для состояния равновессия в А характеристического уравнения имеет вид:

p2-2p+2=0

Отсюда корни характеристического уравнения будут:

Корни комплексные с положительной действительной частью. Следовательно, линейная система первого приближения неустойчива. Значит, в соответствии со второй теоремой Ляпунова, состяние равновессия исходной нелинейной системы в точке А также неустойчиво.

Рассмотрим второе состояние равновессия (точка В). Лианеризованные уравнения имеют вид:

Отсюда хаарктеристическое уравнение будет р²-2=0, его корни р_1,2=2.

Следовательно, состояние равновессия в т. В соответствует седлу, и линеаризованная система неустойчива, а, следователно и исходная нелинейная система в этом состоянии равновесия неустойчива.