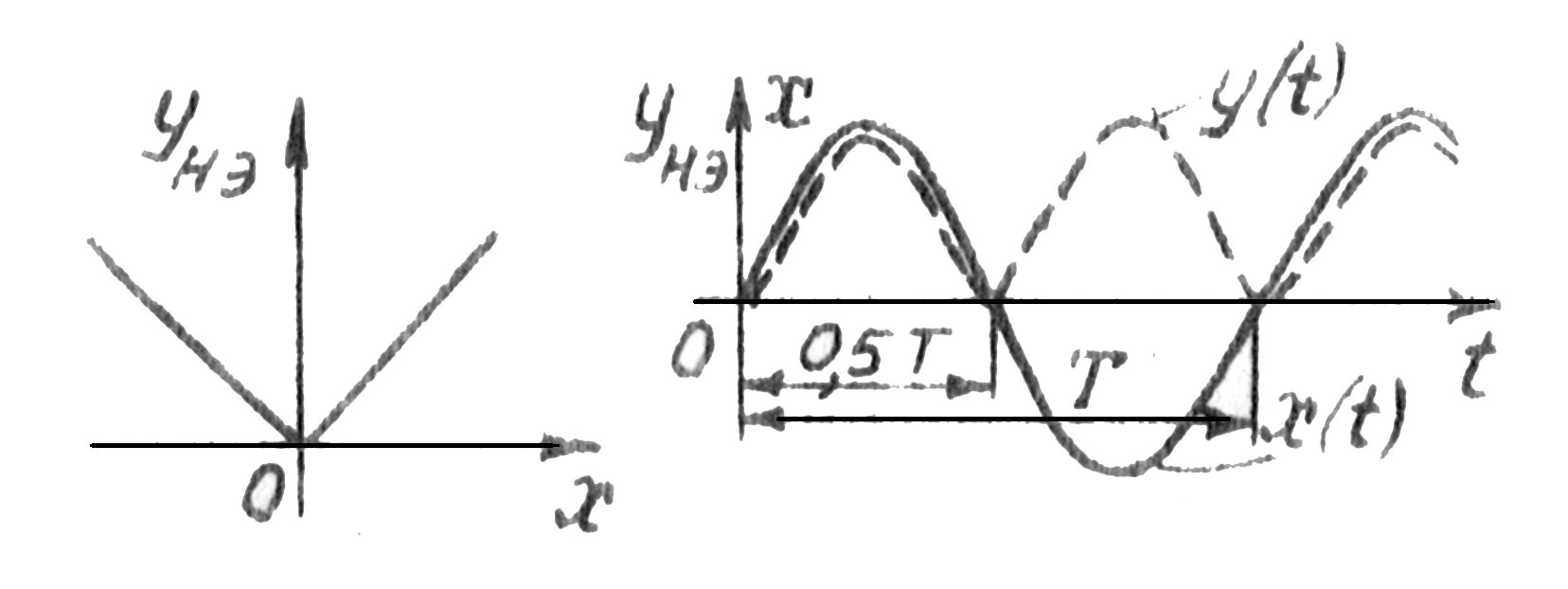лирования, так как одновременно с уменьшением S₁ и ω уменьшается и S₀ (кривая 1).

Расчет интегрального квадратичного критерия для различных процессов регулирования при m=const показал, что минимум I_кв соответствует точке на кривой равной колебательности вблизи от вершины иа правой ветви. На практике рекомендуется выбирать рабочую частоту из соотношения ω_p≈1,2ω⁰ или ω_p≈0,8ω^п,

где ω₀ – частота, соответствующая вершине кривой m=const;

ω^п – частота, соответствующая пропорциональному закону регулирования (рис. 91а).

Таким образом методика расчета оптимальных настроек ПИ-регуля-

-тора сводится к следующему: 1) расчет расширенных частотных характеристик объекта для заданной степени колебательности; 2) построение кривой равной колебательности в плоскости S₁, S₀; 3) выбор ω_p и соответствующих ей S₁^опт и S₀^опт.

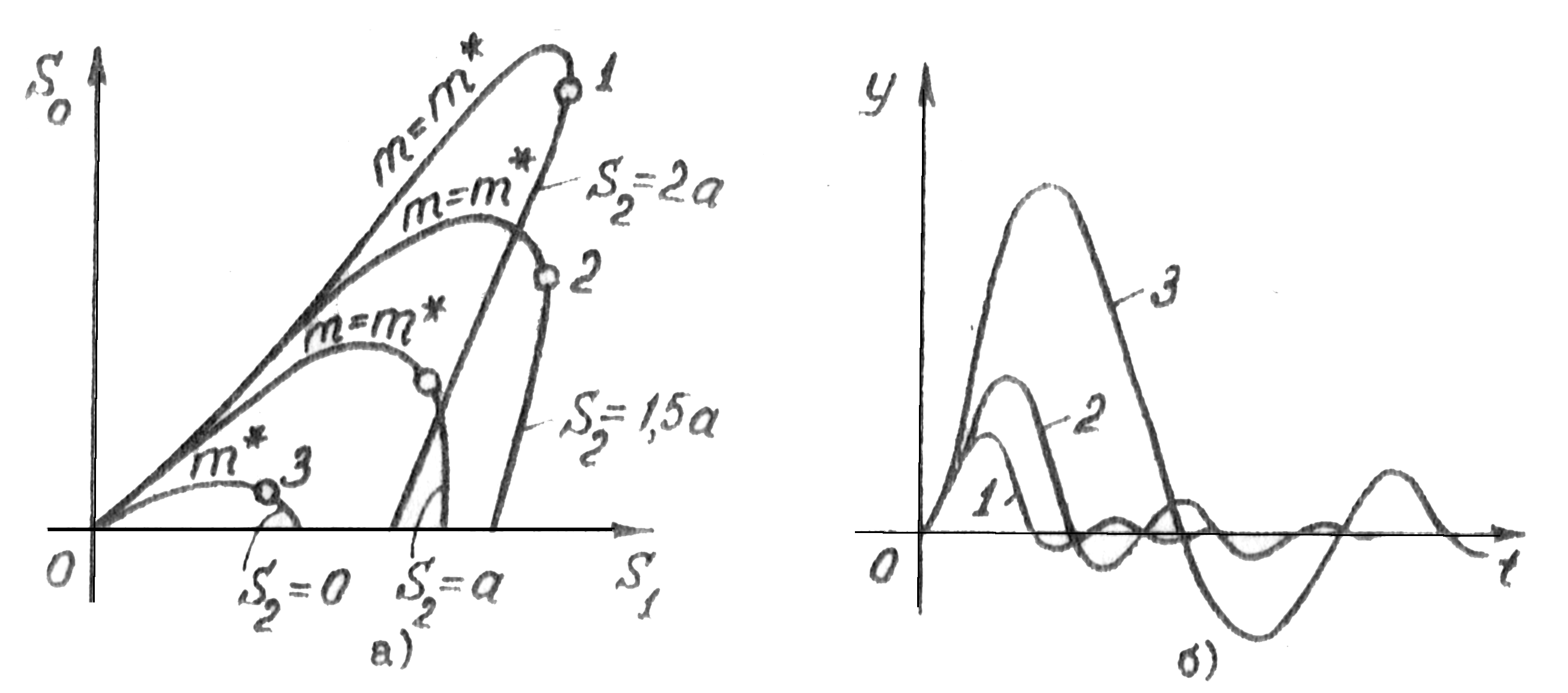
ПИД-регулятор – регулятор с тремя параметрами настройки S₀, S₁, S₂. Вместо плоскости параметров настройки для ПИД-регулятора мы имеем трехмерное пространство. В этом случае определение оптимальных параметров настройки производится в следующем порядке. Задаваясь значением S₂=const, по формулам рассчитывают соот­ветствующие ему S₀ и S₁ и строят кривую равной степени коле­бательности в плоскости S₀S₁. Задаваясь различными значениями S₂ и повторяя расчеты, получают серию кривых равной степени ко­лебательности в плоскости S₀S₁. Характер этих кривых аналогичен уже рассмотренной ранее кривой равной колебательhoctи для ПИ-регулятора (т.е. S₂=0). Для каждого значения S₂ условно оптимальные настройки S₀ и S₁, определяются так же, как и для ПИ-регулятора (рис. 93а).

­­

Рис. 93

Сравнение между собой оптимальных процессов регулирования для различных значений S₂ показывает, что введение дифференциаль­ной составляющей в закон регулирования резко улучшает качество переходных процессов в АСР (рис. 93б); однако, начиная с неко­торых значений S₂, дальнейшее увеличение этого параметра на­стройки мало эффективно. Следовательно выбор оптимального значе­ния S₂^опт и соответствующих ему S₀^опт и S₁^опт должен производиться на основе непосредственного сравнения качества процессов регулирования, соответствующих различным значениям S₂, по интеграль­ному квадратичному критерию Iкв; в качестве оптимальных настро­ек выбираются настройки, обеспечивающие наименьшее по сравнению с другими значение I_кв.

§2. Метод незатухающих колебаний

Рассматриваемый ниже приближенный метод определения оптималь­ных настроек регуляторов, называемый методом незатухающих колеба­ний, был предложен американскими учеными Циглером и Никольсом.

Метод применяется для объектов с запаздыванием. В соответствии с этим методом расчет настроек ПИ- или ПИД-регуляторов проводится в два этапа: 1)расчет критической нас­тройки пропорциональной составляющей S₁^кр (S₀=S₂=0), при которой АСР будет находиться на границе устойчивости; 2)опреде­ление S₁^кр по приближенным формулам оптимальных настроек S₁^опт, S₀^опт, S₂^опт, обеспечивающих для большинства объектов степень затухания 0.75 и сравнительно небольшую динамическую ошибку.

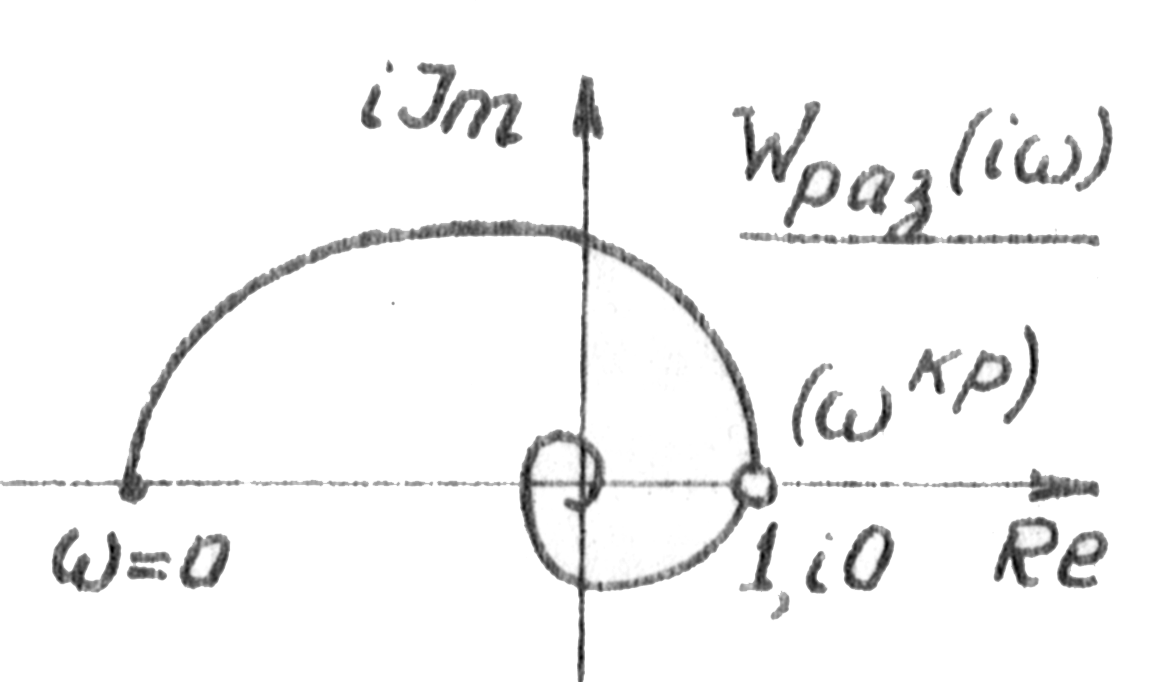
Исходное уравнение для расчета критического значения нас­тройки пропорциональной составляющей S₁^кр выводится из критерия Найквиста, согласно которому при устойчивости разомкнутой системы замкнутая САР будет находиться на границе устойчивости, ес­ли АФХ разомкнутой системы проходит через точку (1,iO) (рис. 116) Т.о. для некоторого значения частоты (обозначим ее ^кр) будет выполняться соотношение

Wраз(iкр)=1

(6-12)

Как видно из (6-12), в отличие от метода расширенных частот­ных характеристик здесь расчет П-регулятора ведется по обычным частотным характеристикам объекта и S₁^кр и ^кр определяются из уравнений

	-об(кр)=;
	.
Рис. 94

Рабочие настройки ПИ и ПИД-регуляторов определяются по найденным S₁^кр и ω^кр по формулам, предложенным Циглером и Никольсом, из которых можно вывести соотношения:

для П-регулятора:

S1=0,5S1кр

(6-13)

для ПИ-регулятора:

S1=0,45S1кр;	(6-14)
S0=0,08S1кркр;

для ПИД-регулятора:

S1=0,6S1кр;

S0=1,9S1кркр;

.

(6-15)

Метод незатухающих колебаний часто используется на прак­тике для экспериментального определения близких к оптимальным настроек регуляторов.

Выше мы рассмотрели методы расчета настроек различных регуляторов. Выбор того или иного типа регулятора определяется в каждом конкретном случае в зависимости от свойств объекта регулирования и динамических характеристик регулятора.

НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ Глава 7. ХАРАКТЕРИСТИКИ НЕЛИНЕЙНЫХ СИСТЕМ

§1. Особенности нелинейных систем

Нелинейными называются системы, которые не подчиняются принципу суперпозиции. Система будет нелинейной, если она содержит хотя бы одно звено, для которого не выполняется принцип суперпо­зиции.

Различают два типа нелинейностей: слабые нелинейности и су­щественные нелинейности. К первой группе относят такие характе­ристики, которые при малом диапазоне изменения координат могут быть заменены линейными зависимостями. Ко второй группе отно­сятся нелинейные характеристики, которые являются существенно нелинейными функциями, например, разрывными или близкими к раз­рывным. Такие характеристики могут быть чаще всего представлены в виде кусочно-линейных функций.

Характер возможных движений в нелинейной системе значительно разнообразнее, чем в линейной. Некоторые особые свойства нелиней­ных элементов нашли применение в технике. Так, в ряде случаев нелинейные регуляторы (например, регуляторы с переменной струк­турой, т.е. регуляторы, у которых закон регулирования изменя­ется в зависимости от величины отклонения регулируемой коорди­наты и её производных) оказываются существенно более эффектив­ными для управления. На нелинейных свойствах основано выпрям­ление переменного тока, генерирование электромагнитных колеба­ний, ведение технологического процесса в колебательном режиме, когда в силу нелинейности характеристик процесса производитель­ность аппарата, в котором он реализован, оказывается выше, чем при стационарном управлении.

В других случаях нелинейность характеристик приводит к вред­ным последствиям. При этом либо приходится искать пути устране­ния нелинейностей, либо так выбирать режим функционирования системы, чтобы нелинейности меньше сказывались на результатах работы.

Отметим некоторые характерные особенности нелинейных систем по сравнению с линейными. Все эти особенности вытекают из основ­ного свойства нелинейных систем – неподчинение принципу суперпозиции.

Линейные системы	Нелинейные системы
1. При подаче на вход линейной системы гарнонического сигнала на ее выходе также устаиавливаются гармонические колебания с той же частотой, которую имеют входные колебания.	1. Вынужденные колебания в нелинейных системах могут отличаться от входного гармони-ческого сигнала как по форме, так и по частоте. Например, для нелинейного элемента со статической характеристикой yнэ=|х| вынужден-ные коле­бания не являются гармоническими коле­баниями и их период вдвое меньше, чем период входных колебаний.
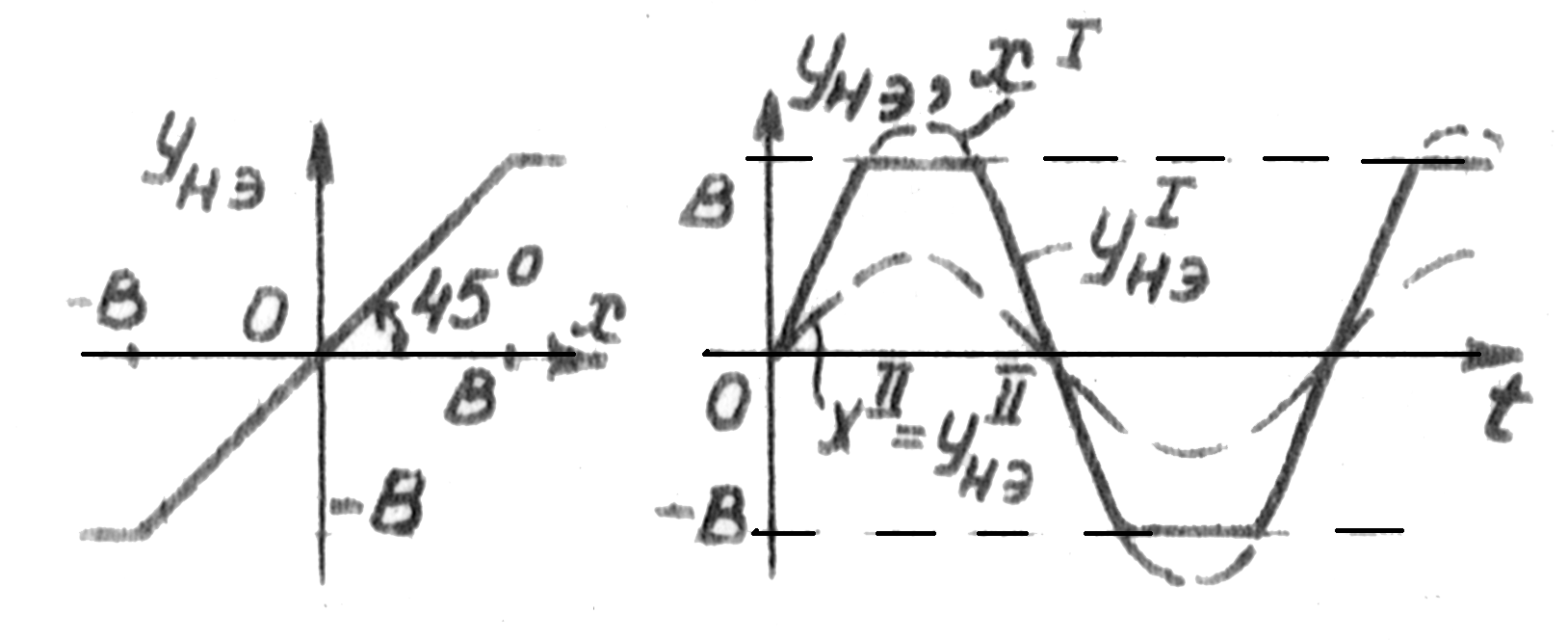
2.Частотные характе­ристики линейных сис­тем на зависят от амплитуды входного сиг­нала и полностью оп­ределяются свойствами системы.	2.Частотные характеристики существенно зависят от амплитуды входного сигна­ла. Так, нелинейный элемент со статичес­кой характеристикой, представленной на рисунке, при малой амплитуде входного сигнала (AB) ведет себя как линейное звено, а при больших амплитудах входного сиг­нала (A>B) выходные колебания искажа­ются
З. Если линейная система устойчива (или неустой­чива), то она устойчива (или неустойчива) при любых начальных усло­виях. Поэтому в каждой линейной системе возможен только один тип движения: в устойчивой системе - асимптоти­ческое приближение к состоянию равновесия, в неустойчивой систе­ме - удаление от сос­тояния равновесия.	3. Нелинейная система может быть ус­тойчивой “малом” или устойчивой “в большом”. В первом случае при малых начальных отклонениях система ведет се­бя как устойчивая, а при значительных отклонениях - как неустойчивая сиcтема. Таким образом в нелинейных системах устойчивость состояния равновесия зависит от начальных условий. Поэтому в нелинейных системах возможны различные типы движения в зависимости от началь­ных условий.
4. Незатухающие колебания в линейной системе возможны только тогда, когда система находться на границе устойчивости, причем амплитуда свободных колебаний определяется начальными условиями.	4. В нелинейных системах возможны незатухающие колебания, амплитуда и частота которых не зависит от начальных условий и определяется свойствами системы. Такие колеба-ния называются автоколебаниями. Примерами автоколебательных сис-тем являются часы, электрический звонок; автоколебания наблюдаются также при определенных условиях в системах автоматического регули-рования, содержащих нелинейные элементы.