Лекция "ГРАФИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ"

ГРАФИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Рассмотрим задачу линейного программирования с двумя переменными x₁ и x₂:

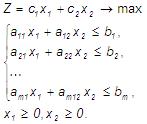
Графический способ решения задачи линейного программирования состоит из двух этапов.

1. Построение области допустимых решений удовлетворяющих всем ограничениям;

2. Поиск оптимального решения среди угловых точек области допустимых решений.

Область допустимых решений, удовлетворяющая системе неравенств

при этом прямая будет перемещаться параллельно самой себе в направлении возрастания. Определив направление возрастания, найдем точку, в которой функция Z принимает максимальное значение. Это значение будет достигаться в одной из угловых точек многоугольника допустимых решений (или на одной из его сторон, в случае если линия уровня совпадет с этой стороной). Поэтому будем осуществлять параллельный перенос линии уровня по области допустимых решений пока не выйдем на ее границу и попадем в угловую точку многоугольника. Координаты этой точки определяются решением системы уравнений, соответствующих прямых.

Подставив найденные координаты в функцию Z, найдем ее максимум, т.е. оптимальное решение.

Замечание. Если исходная задача содержит неравенства типа ≥, то они легко трансформируются в неравенства типа ≤ умножением на (-1). Такую же процедуру можно произвести и с целевой функцией Z, если в исходной задаче ищется ее минимум. Однако можно и не прибегать к этому приему, а просто определить направление убывания функции аналогично тому как определялось направления возрастания, только значения Z брать меньше нуля.

Пример. Решить графически задачу линейного программирования:

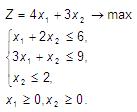
На первом этапе графического решения изображаем множество G допустимых решений. Для этого неравенства системы ограничений переписываем в виде уравнений

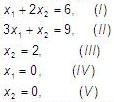
и строим на координатной плоскости прямые соответствующие этим уравнениям. Для каждой прямой выбираем полуплоскость, соответствующую знаку неравенства (направление показано стрелкой). В результате получаем многоугольник решений ОАВСD (рис.1).

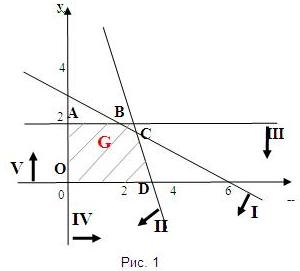
Среди точек многоугольника найдем точку, в которой линейная функция принимает максимальное значение. Для этого построим линии уровня линейной функции Z (пунктирные линии).

Первой построим линию уровня Z=0, проходящую через начало координат (рис. 2).

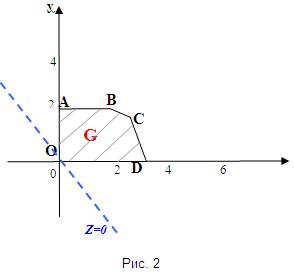
Чтобы определить направление возрастания, изобразим еще одну линию Z=8, проходящую через множество решений системы ограничений. Далее, определив направление возрастания (обозначим стрелкой =>) линейной функции, будем производить параллельный сдвиг линии уровня до тех пор, пока не попадем на границу множества решений. Оптимальное решение будет  в угловой точке С, находящейся на пересечении прямых I и II (рис. 3).

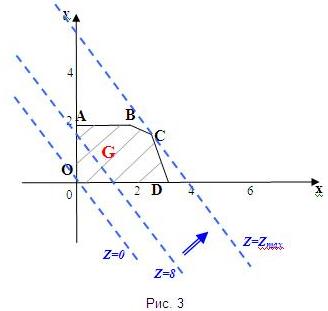
Координаты точки С определяются решением системы уравнений:

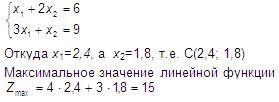
Ответ:   x₁=2,4,  x₂=1,8,  Z_max=15

Лекция "решение задач линейного программирования симплекс-методом" решение задач линейного программирования симплекс-методом

Процедуру решения задач линейного программирования симплекс-методом удобно оформлять в виде симплекс-таблиц. Для этого задачу линейного программирования приводят к стандартной форме, когда система ограничений состоит из одних уравнений и все переменные неотрицательны, а целевая функция стремится к максимуму. Неравенства любого типа (≤ или ≥) можно преобразовать в равенства путем добавления в левую часть неравенств дополнительных переменных (со знаком «плюс» или «минус»). Переход от минимума к максимуму в целевой функции осуществляется умножением на (-1), т.е. min Z= – max (-Z).

Рассмотрим задачу линейного программирования в виде: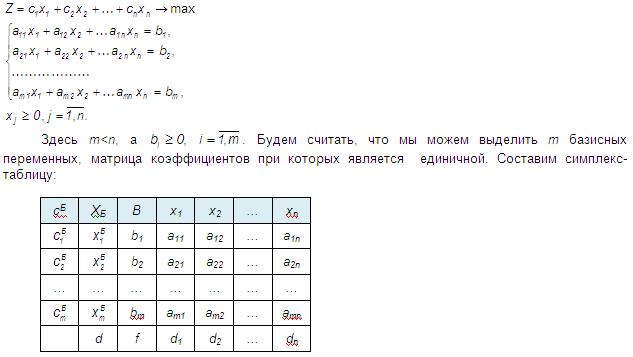

В столбец X_Б записываются базисные переменные соответствующие каждому из уравнений. В столбец с^Б записываются коэффициенты при базисных переменных в целевой функции (присутствует только в начальной таблице, в последующих не пишется). Столбец В заполняется свободными членами из уравнений системы ограничений.

где c_j – коэффициент при переменной x_j в целевой функции.

В дальнейшем каждая симплекс таблица будет отражать одну итерацию симплекс-метода.

Алгоритм симплекс-метода

Если же в исходной задаче стандартного вида нет базисных переменных с единичной матрицей коэффициентов, то применяют метод искусственного базиса. Пусть, для определенности, в первых s уравнениях системы ограничений отсутствует единичная матрица коэффициентов (это всегда можно сделать простой перестановкой уравнений). Построим новую вспомогательную задачу.

Так как во втором и третьем уравнениях нет единичной матрицы переменных, воспользуемся методом искусственного базиса и введем переменные y₁ и y₂, целевая функция при этом тоже изменится.

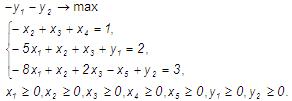
Составим симплекс-таблицу.

В столбец X_Б вписываем переменные составляющие базис. В столбец с^Б коэффициенты при базисных  переменных в целевой функции. Остальные столбцы заполняем данными из системы ограничений (коэффициентами при соответствующих переменных). В строку d вписываем оценки вычисленные по формулам: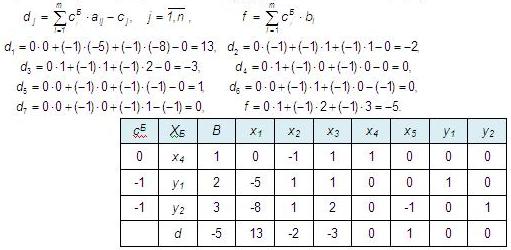

Среди оценок есть отрицательные, значит решение не оптимально. Минимальная среди оценок -3, переменная x₃ в базис войдет. Далее вычисляем оценочные отношения для этого столбца (делим построчно элементы столбца В на положительные элементы столбца x₃) и выбираем минимальное равное 1. Следовательно, переменная x₄ из базиса выйдет. Выделенный элемент будет разрешающим:

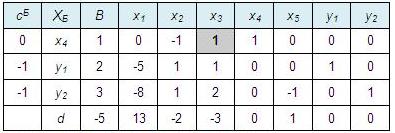
Преобразуем симплекс-таблицу, отбросив столбец с^Б:

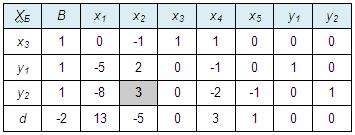
Среди оценок опять есть отрицательные, поэтому продолжим преобразования:

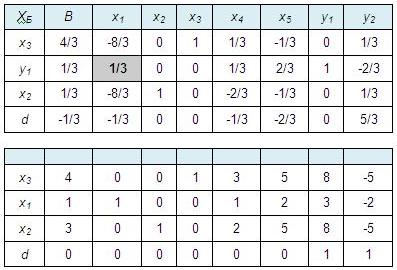
Все оценки неотрицательные, искусственные переменные вышли из базиса, а значение функции равно 0. Теперь можно отбросить столбцы, содержащие искусственные переменные, и пересчитать оценки в соответствии с целевой функцией

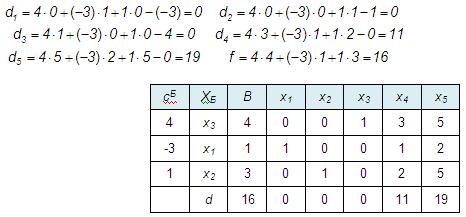
Все оценки снова получились неотрицательные, следовательно, решение оптимально:

x₁ =1, x₂ =3, x₃ =4, а максимум функции равен 16.

Поскольку исходная задача была на минимум, то надо умножить значение целевой функции на (-1). Получим Z_min = –16.

Ответ:   x₁=1,  x₂=3,  x₃=4,  Z_min= –16

РЕШЕНИЕ ЗАДАЧ ЦЕЛОЧИСЛЕННОГО ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ МЕТОДОМ ГОМОРИ

Сущность метода Гомори решения задачи целочисленного линейного программирования состоит в том, что сначала задача решается без условия целочисленности. Если полученное решение целочисленное, то задача решена. В противном случае к ограничениям задачи добавляется новое ограничение, обладающее следующими свойствами:

• оно должно быть линейным;

• должно отсекать найденное оптимальное нецелочисленное решение;

• не должно отсекать ни одного целочисленного решения.

Далее задача решается с учетом этого нового ограничения. После этого в случае необходимости добавляется еще одно ограничение и т.д.

Рассмотрим задачу целочисленного линейного программирования вида:

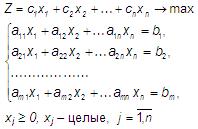
Будем решать ее без условия целочисленности симплекс-методом. Если в результате полученное оптимальное решение окажется целочисленным, вычисления заканчиваем.

В противном случае строим  дополнительное ограничение. Для этого среди элементов столбца В финальной симплекс-таблицы ищем нецелочисленные, если таких несколько, то берем максимальное b_s и составляем дополнительное ограничение по строке s:

Далее введением дополнительной неотрицательной целочисленной переменной преобразуем это неравенство в уравнение:

Включаем его в симплекс-таблицу и решаем двойственным симплекс-методом.

Алгоритм двойственного симплекс-метода

Получив оптимальное решение, проверяем его на целочисленность и если оно окажется не целочисленным, повторяем процедуру с дополнительным ограничением.

Пример. Решить методом Гомори задачу целочисленного линейного программирования:

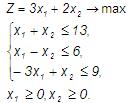
x₁,x₂ – целые числа

Решение:

Сначала решим симплекс-методом задачу без учета условия целочисленности. Для этого приведем ее к стандартному виду:

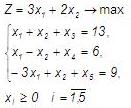
Составим симплекс-таблицу, в столбец X_Б вписываем переменные составляющие базис. Остальные столбцы заполняем данными из системы ограничений (коэффициентами при соответствующих переменных):

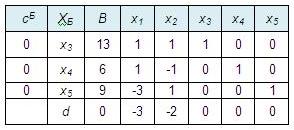
В строку d вписываем оценки вычисленные по формулам:

Среди оценок есть отрицательные, значит решение не оптимально. Минимальная среди оценок -3, переменная x₁ в базис войдет. Далее вычисляем оценочные отношения для этого столбца (делим построчно элементы столбца В на положительные элементы столбца x₁) и выбираем минимальное равное 6. Следовательно, переменная x₄ из базиса выйдет. Выделенный элемент будет разрешающим:

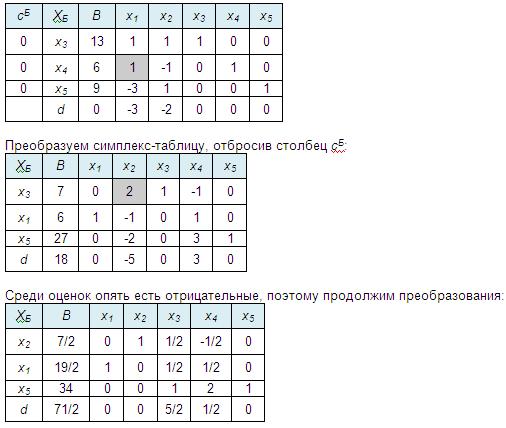
Все оценки получились неотрицательные, следовательно, из этой таблицы получаем x₁ =19/2, x₂ =7/2, т.е. решение не целочисленное, поэтому строим дополнительное ограничение по второй строке (ей соответствует максимальное нецелое значение из столбца b):

Получим целочисленное решение x₁=9,  x₂=4

Ответ:   x₁=9,  x₂=4,  Z_max= 35

Начало формы