Статистические свойства мнк оценок.
Несмещённость оценок: как следует из результатов анализа МНК оценок в линейной задаче МНК-оценки не смещены, если отсутствует систематическая составляющая ошибок измерений
Эффективность оценок: Согласно теореме Гаусса-Маркова несмещённая МНК-оценки обладают минимальной дисперсией, т.е. являются эффективными в классе всех линейных несмещённых оценок, другими словами в принципе можно отыскать оценки лучшие чем МНК оценки (при соблюдении исходных допущений относительно условий опыта), но только в нелинейных задачах оценивания.
Закон распределения МНК-оценок: т.к. оценки представляют собой величины, наиболее полные заключения о них заключены в вероятностном законе распределения. При произвольном распределении ошибок измерений о Законе распределения оценок вообще говоря однозначно судить невозможно. Однако, в линейной задаче оценивания МНК-оценки получаются в результате линейного преобразования измерительной информации , где
В
теории вероятностей доказано, что если
вектор z
распределён по нормальному закону, то
его линейное преобразование (в данном
случае с помощью матрицы D)
даёт нормально распределённый вектор
оценок
. Для других законов распределения z
подобного заключения не получено. Однако
известно, в соответствие центральной
предельной теоремой Ляпунова, при
большом числе измерений распределение
оценки
является асимптотически нормальным,
таким образом, во многих практических
ситуациях знания математического
ожидания и корреляционной матрицы
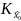достаточно для полной характеристики
вектора оценок
,
однако, следует иметь ввиду, что для
соблюдения выводов центральной предельной
теоремы необходимо как минимум два
ограничения, чтобы 1) ошибки измерений
были попарно независимы и 2) имели
примерно одинаковые дисперсии.
Лекция 5 08.11.2013
Общий вид алгоритма оценивания.
(Для нелинейного случая)
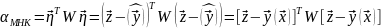
Рамзерности:
N*1
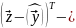1*N
N*N
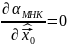
В отличие от динамической фильтрации тут используется совокупность измерений.
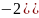
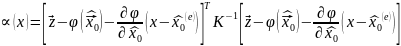
Мы пришли к линейной задаче.
Задача решается многоитерационным способом. Оценка вектора состояния полностью определяется знанием:
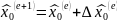
Алгоритм получения нелинейной мнк-оценки
Экспликация (разъяснения некоторых значений в алгоритме или рисунке)
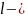номер
итерации решения получения нелинейной
МНК-оценки
число
моментов измерений
Условие окончания процесса последовательных приближений
А) Одновременное выполнение всех неравенств типа:
Б) Выполнение неравенства
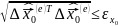
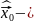содержит
однородные компоненты
В)
И т.д.
При нарушении условия выхода из итерационного процесса (невыполнении указанных неравенств) счётчику числа итераций присваивается очередной знак итерации и вычисления повторяются со второго пункта, а если прошло значительное время и задача не сходится (нет выхода)
Вводится принудительная сходимость. Выводится из цикла при реакции оператора.
Причины «расхождения» (несхождения) оценок:
Неверный выбор начального приближение
.
Разложение в ряд Тейлора не соответствует
реалиям.Плохая обусловленность задачи оценивания.
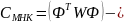вырождена
число
обусловленностей матрицы Грамма
(отношение максимального к минимальному
числу обусловленностей матрицы)
Наличие аномальных измерений (или сеансов измерений)
Неверные априорные данные об ошибках измерений и о ММД (например мы уточняем орбиту а там не правильно учтено световое давление). Частные производные будут считаться неверно. (ЧП)
Некорректный выбор метода расчёта частных производных
Неверный выбор шага интегрирования при применении численного интегрирования.
Точность МНК-оценок:
В отличие от линейных задач оценивания математическое ожидание и коварционная матрица здесь явном виде получены быть не могут. Их элементы рассчитываются с помощью метода статистических испытаний, что связано с большими вычислительными затратами.
Статистические свойства оценок. Свойства МНК-оценок в нелинейных задачах оценивания также исследуются с помощью метода статистических испытаний и зависят от вида используемых математических моделей.
Для сокращения вычислительных затрат матрица Ф может обновляться не на каждой итерации, а например через 1.
Лекция 6 15.11.2013