МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РК

РВУЗ «КРЫМСКИЙ ГУМАНИТАРНЫЙ УНИВЕРСИТЕТ» (г.Ялта)

Кафедра математики, теории и методики обучения математике

А.А. Бубнова

Методические указания «математика»

г.Ялта, 2014 г.

СОДЕРЖАНИЕ

1. ЧИСЛОВЫЕ СИСТЕМЫ

- Различные числовые множества. Метод математической индукции

- Действия над действительными числами

- Модуль числа. Числовая прямая

- Отношения. Пропорция. Проценты

2. ФУНКЦИИ

- Определение, виды и свойства функций

- Построение графиков элементарных функций

- Тригонометрия

3. ПРОИЗВОДНАЯ И ИНТЕГРАЛ

- Производная, таблица производных

- Первообразная. Таблица интегралов

- Определённый интеграл. Формула Ньютона-Лейбница

4. КОМБИНАТОРИКА

- Перестановки, размещения и сочетания без повторений

- Перестановки, размещения и сочетания с повторениями

- Бином Ньютона

5. СТАТИСТИКА

- Сбор информации для статистики

- Вариационный ряд. Распределение ряда

- Математические параметры статистического распределения

6. ВОПРОСЫ К ЭКЗАМЕНУ. ВАРИАНТ КОНТРОЛЬНОЙ РАБОТЫ

7. ЛИТЕРАТУРА

1. Числовые системы Действительные числа

Натуральные числа. Числа, которые используются для счета предметов: 1, 2, 3, ... . N = {1, 2, 3, ...} - множество натуральных чисел.

Целые числа. Натуральные числа 1, 2, 3, ... и число 0 образуют множество целых чисел. Z = {..., -3, -2, -1, 0, 1, 2, 3, ...} - множество целых чисел.

Рациональные числа. Числа которые можно представить в виде nmm Z n N, называют рациональными.Q = N + Z + {nmm Z n N} - множество рациональных чисел.

Замечание. Любое рациональное число - бесконечная периодическая десятичная дробь

Иррациональные числа. Числа, которые нельзя представить в виде nmm Z n N, называют иррациональными. I = { 7 73  } - иррациональные числа

Замечание. Любое иррациональное число - бесконечная непериодическая десятичная дробь.

Действительные числа. объединение рациональных и иррациональных чисел называют действительтными числами. Множество действительных чисел обозначают символом R.R Q Z N

Замечание. Любое действительное число - бесконечная десятичная дробь.

Действительные числа и числовые множества

     Множества 

     Натуральных чисел: 

     Целых чисел: 

     Рациональных чисел: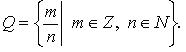 

     Действительных (вещественных) чисел: 

     Числовые промежутки 

     Отрезок (замкнутый промежуток, сегмент):

  Интервал (открытый промежуток):

     Полуинтервалы:

     Бесконечные числовые промежутки (лучи, полупрямые):

     Числовая прямая: 

     Замечание. Наряду с приведенными используются и обозначения   - для интервала;  - для полуинтервалов;   - для лучей;   - для числовой прямой.

Процент. Сложный процент

Процентом называется сотая часть от числа, т.е. 1%А = 0,01А

1% = 0,01, 2% = 0,02, 45% = 0,45, 350% = 3,5. Часто встречающиеся проценты: 5% = 0,05 = 120, 10% = 0,1 = 110, 20% = 0,2 = 51, 25% = 0,25 = 41, 50% = 0,5 = 21, 75% = 0,75 =43

Основные типы задач.

1. Сколько процентов составляет число А от числа В? 

Решение: x=ВА 100%

2. Число А увеличилось на 20%, а затем полученное число уменьшилось на 25%. Как, в итоге, изменилось исходное число?

 Решение: 1) А₁= (100% + 20%)А = 120%А = 1,2А 2) А₂= (100% - 25%)А₁ = 75%А₁ = 0,75А₁ = 0,75 1,2А = 0,9А = 90%А 3) А₂ - А = 90%А - 100%А = -10%. Ответ: число уменьшилось на 10%.

3. Как изменится время, если скорость движения увеличится на 25%?

 Решение: 1)t=SV 2) t1=SV1=S1 25V=11 25SV=0 8SV=80%t. Ответ: уменьшится на 20%.