МБОУ «Лицей г. Абдулино»

XIII научно-практическая конференция «Старт в науку»

Секция: математика

«Решение квадратных уравнений»

Работу выполнила:

Сергеева П.С.

Учащаяся 8 «А» класса

МБОУ «Лицей г.Абдулино»

Руководитель:

Ягодкина Зоя Геннадьевна

Учитель математики

МБОУ «Лицей г.Абдулино»

2014 г.

Содержание

I.Введение - 3       

1. Цели и задачи - 3

2. Актуальность - 3

II.Теоретическая часть - 5-11

1. Понятие квадратного уравнения – 5

2. Из истории квадратных уравнений – 5-6

3. Способы решения квадратных уравнений – 7-11

3.1 Свойства коэффициентов – 7

3.2 Решений квадратных уравнений с помощью циркуля и линейки – 8-9

3.3 Геометрический способ решения - 9

3.4 Решение квадратных уравнений методом «переброски» - 10

3.5 Решение квадратных уравнений с помощью номограммы – 10-11

III. Практическая часть – 12

1. Социологическое исследование среди 8-9 классов нашей школы на предмет решения квадратных уравнений - 12

2. Разработка буклета - 12

3. Создание справочника по способам решения квадратных уравнений -12

IV. Заключение – 13

V. Литература - 14

I.Введение

Цель работы:

Познакомиться с новыми способами решения квадратных уравнений и формировать умение выбора рационального способа решения квадратных уравнений.

Задачи:

• Изучить литературу по проблеме.

• Расширить и углубить знания по математике, познакомившись со способами решения квадратных уравнений.

• Изучить различные способы решения.

• Распространение различных способов.

Актуальность.

Квадратные уравнения находят широкое применение при решении задач различного уровня сложности. Решение задач с помощью уравнений – это один из самых рациональных способов. Поэтому умение составлять и решать уравнения - важный навык выпускника.

Мне пришла идея рассмотреть те способы решения квадратных уравнений, на которые недостаточно времени уделено на уроках или совсем не рассматриваются в школьном курсе. В последние годы учащиеся сдают региональные экзамены в 7-8-х классах, ГИА и ЕГЭ по математике, которые проводятся в форме тестирования. Поэтому учащиеся должны уметь быстро ориентироваться среди данных вариантов ответов, а для этого надо знать и уметь применять эффективные способы решения. Решение через дискриминант трудоемкий способ и требует много времени. А ведь наверняка существуют другие способы, которые более просты в оформлении, а некоторые дают возможность решать уравнение устно. Это сэкономило бы время на экзамене.

Поэтому я решила изучить другие способы решения квадратных уравнений, которых нет в школьном курсе алгебры. Познакомить с ними одноклассников, чтобы у меня и у них была возможность выбора рационального способа решения.

Проблема моего исследования видится в необходимости изучения, а также освоении различных способов, которые способствуют развитию умственных способностей и математического кругозора ученика.

Объект исследования: раздел математики «Уравнения».

Предмет исследования: квадратные уравнения

Гипотеза:

Предполагаю, что освоение новых методов решения квадратных уравнений позволит выбирать самый рациональный способ для их решения.

Методы исследования:

• Изучение программного материала по учебникам А.Г.Мордковича, Н.В.Алимова, Ю.Н.Макарычева

• Изучение дополнительного материала по энциклопедиям

• Изучение исторического материала по сайтам Интернета

• Работа в программах Microsoft Word, Excel, PowerPoint, Publisher

II. Теоретическая часть

1.Что такое квадратное уравнение?

Квадратное уравнение – уравнение вида ax² + bx + c = 0,где х- переменная, а,b и с-некоторые числа, причем, а ≠ 0.

Если в квадратном уравнении ах² + bx + c = 0 хотя бы один из коэффициентов b или с равен нулю, то такое уравнение называют неполным квадратным уравнением.

Неполные квадратные уравнения бывают трёх видов:

1) ах² + с = 0, где b ≠ 0;

2) ах² + bх = 0, где с ≠ 0;

3) ах² = 0.

2.Из истории квадратных уравнений:

Необходимость решать уравнения еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земли, а также с развитием астрономии и математики.

Применяя современную алгебраическую запись, можно сказать, что в их  клинописных текстах  встречаются неполные и полные квадратные уравнения.

Впервые квадратное уравнение сумели решить математики Древнего Египта, сводя их решение к геометрическим построениям.

Приемы решения уравнений без обращения к геометрии дает Диофант Александрийский.

Способ решение полных квадратных уравнений Диофант изложил в книгах «Арифметика», которые не сохранились.

Правило решения квадратных уравнений, приведенных к виду, где a > 0, дал индийский ученый Брахмагупта.

Мухаммед бен Мусы аль-Хорезми, багдадский ученый IХ в. При решении полных квадратных уравнений аль-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.

Трактат аль-Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.

Общее правило решения квадратных уравнений было сформулировано немецким математиком М. Штифелем (1487 - 1567).

Знаменитый французский ученый Франсуа Виет был по профессии адвокатом. В 1591 г. впервые ввел буквенные обозначения и для неизвестных, и для коэффициентов уравнений. Однако свое утверждение он высказывал лишь для положительных корней (отрицательных чисел он не признавал).

После трудов нидерландского математика А. Жирара (1595-1632), а также Декарта и Ньютона способ решения квадратных уравнений принял современный вид.

В учебнике алгебры 8 класса под редакцией С. А. Теляковского основное внимание уделяется решению уравнений вида , по формуле корней. Рекомендуется ознакомить учащихся с формулами Виета, выражающими зависимость между корнями квадратного уравнения и его коэффициентами . Теорема Виета не относится к обязательному материалу.

В учебнике алгебры 8 класса, автор Мордкович А.Г., излагает решение квадратных уравнений, используя метод разложения левой части уравнения на множители, метод выделения полного квадрата, графическим способом, по формуле корней и теореме Виета.

Я решила подробно рассмотреть те способы, которых нет в данных учебниках.

3.Способы решения квадратных уравнений

3.1 Свойства коэффициентов

Первое свойство коэффициентов

Второе свойство коэффициентов

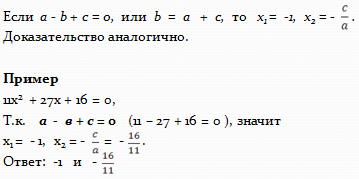
Третье свойство коэффициентов