Министерство образования науки и образования Российской Федерации

Новосибирский государственный технический университет

Кафедра ВТ

Расчётно-графическое задание

по дисциплине «Моделирование»

«Моделирование процесса работы производственной линии»

Вариант #34

Факультет: АВТФ

Группа: АВТ-109

Выполнил: Проверила: Альсова О.К.

Новосибирск

2013

Реферат

Пояснительная записка к курсовой работе на тему “Моделирование процесса функционирования вычислительной системы” представлена на 29 страницах. Пояснительная записка состоит из 10 глав; содержит 2 таблицы, 13 рисунков, 2 приложения. Список литературы включает 1 библиографический источник.

Имитационное моделирование, математическое ожидание, критерий согласия хи-квадрат, гистограмма, закон распределения, дисперсия, критерий Фишера, диаграмма рассеяния, закон распределения, корреляционная матрица.

Результатом выполнения расчётно-графического задания является разработанная программа, имитирующую работу заданной системы массового обслуживания; анализ результатов её и определение методов усовершенствования системы. В ходе курсовой работы выполнен обзор теоретического материала, использованного для решения поставленной задачи; сформулировано техническое задание на разработку программы; смоделирована работа системы; определены основные достоинства и недостатки данной системы; предложены и реализованы варианты оптимизации работы системы.

Оглавление

1. Постановка задачи

В цех на участок обработки поступают партии деталей по три в каждой. Интервалы между приходами деталей равномерно распределены в интервале 30±10 минут. Первичная обработка деталей происходит на одном из станков двух типов. Деталь поступает на обработку на станок с меньшей очередью. Станок первого типа обрабатывает деталь в среднем за 30 минут (закон распределения экспоненциальный) и допускает 6% брака, второго типа соответственно в среднем 20 минут и 10% брака. Количество станков первого типа – 3, второго типа – 2. Все бракованные детали возвращаются на повторную обработку на свой станок. Детали, которые были забракованы дважды, считаются отходами и отправляются на утилизацию.

После первичной обработки детали поступают в накопитель, а из него во вторичную обработку, которую проводят два параллельно работающих станка третьего типа за время, распределенное по нормальному закону со средним 25 минут и среднеквадратическим отклонением 2 минуты. Причем второй станок третьего типа подключается к работе, только если в накопителе находится более трех деталей. Затраты на содержание станков первого, второго и третьего типов составляют соответственно 4, 3, 1.5 единиц стоимости в час, независимо от того, используется станок или нет. Цена реализации готовой детали составляет 200 единиц стоимости, а стоимость покупки необработанной детали – 45 единиц стоимости.

Есть возможность повысить качество первичной обработки деталей. Уменьшение уровня брака в работе станков на r процентов требует дополнительных затрат r*4 единиц стоимости на каждую деталь. Действия по повышению эффективности качества первичной обработки могут проводиться для обоих типов станков независимо друг от друга.

Смоделировать процесс обработки 1000 партий деталей. Определить характеристики очереди деталей, количество забракованных деталей, коэффициенты использования станков, прибыль цеха.

2. Обзор методов и средств решения задачи

Общие сведения об имитационном моделировании систем

С развитием вычислительной техники широкое применение получили имитационные методы моделирования для анализа систем, преобладающими в которых являются стохастические воздействия. Суть ИМ заключается в имитации процесса функционирования системы во времени, соблюдением таких же соотношений длительности операций как в системе оригинале. При этом имитируются элементарные явления, составляющие процесс; сохраняется их логическая структура, последовательность протекания во времени. Результатом ИМ является получение оценок характеристик системы.

Имитационное моделирование – это процесс конструирования модели реальной системы и постановки экспериментов на этой модели с целью либо понять поведение системы, либо оценить (в рамках ограничений, накладываемых некоторым критерием или совокупностью критериев) различные стратегии, обеспечивающие функционирование данной системы. Все имитационные модели используют принцип черного ящика. Это означает, что они выдают выходной сигнал системы при поступлении в нее некоторого входного сигнала. Поэтому в отличие от аналитических моделей для получения необходимой информации или результатов необходимо осуществлять "прогон" имитационных моделей, т. е. подачу некоторой последовательности сигналов, объектов или данных на вход модели и фиксацию выходной информации, а не "решать" их. Происходит своего рода "выборка" состояний объекта моделирования (состояния - свойства системы в конкретные моменты времени) из пространства (множества) состояний (совокупность всех возможных значений состояний). Насколько репрезентативной окажется эта выборка, настолько результаты моделирования будут соответствовать действительности. Этот вывод показывает важность статистических методов оценки результатов имитации. Таким образом, имитационные модели не формируют свое собственное решение в том виде, в каком это имеет место в аналитических моделях, а могут лишь служить в качестве средства для анализа поведения системы в условиях, которые определяются экспериментатором.

Метод наименьших квадратов

Предположим, что между экспериментальными данными предполагается линейная зависимость:

(2.2.1)

Зависимость (2.2.1) носит название линейной регрессии. Исходные данные для получения оценок параметров модели (2.3.1) обычно записывают в виде матриц:

,

где i – номер эксперимента, N – их количество.

Для того чтобы функция регрессии (2.2.1) достаточно хорошо описывала эмпирическую зависимость, ее параметры подбирают таким образом, что отклонения между измеренными и теоретическими значениями принимали бы минимальные значения. В качестве такого критерия выбирают сумму квадратов отклонений:

(2.2.2)

Выбор критерия в таком виде объясняется тем, что при этом формулы расчета значений достаточно просты, хорошо зарекомендовали себя в практике, а сами эти значения обладают определенными свойствами. Критерий (2.2.2) является обобщенным показателем рассеивания вокруг искомой линейной зависимости.

Параметры подбирают из условий минимизации (2.2.2). Необходимым условием существования минимума критерия (2.2.2) является равенство нулю частных производных по неизвестным параметрам . Минимизируя функцию Q положим

(2.2.3)

система линейных уравнений (2.3.3), как это легко найти, в матричной форме записывается

(2.2.4)

Из (2.3.4) следует, что

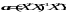(2.2.5)

Оценку , найденную по формуле (2.3.5) называют оценкой наименьших квадратов, или оценкой МНК.

Критерий Фишера

Оценкой качества всей модели в целом может служить критерий Фишера [2]: если (2.3.1) то уравнение в целом не значимо. Здесь - критическая граница распределения Фишера с степенями свободы соответствующая уровню значимости р; - среднее значение . Вычисление отношения (2.4.1) позволяет выявить, насколько существенно различие этих двух показателей, т.е. в какой мере замена на улучшает наши представления о характере зависимости.

Применение Ф-критерия дает возможность конкретно оценить действительную связь между переменными. Если условию Фишера удовлетворяют несколько моделей, то предпочтение отдают наиболее простым аналитическим выражениям.

Алгоритм проверки значимости выборочных коэффициентов регрессии

Известна формула, позволяющая вычислить - оценку дисперсии оценок :

(2.4.1)

где - диагональный элемент матрицы: [3]. Соотношения (2.4.1) позволяют проверять гипотезы о значимости выборочных коэффициентов регрессии. Если расчетная значимость j – ого коэффициента

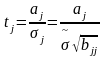(2.4.2)

меньше по модулю теоретической значимости , то теоретический коэффициент регрессии принимается равным нулю , с вероятностью ошибки . Здесь - значение - статистики Стьюдента с доверительной вероятностью и степенями свободы.

Известен алгоритм последовательного исключения факторов из модели. На каждом этапе рассчитываются эмпирические значимости всех коэффициентов регрессии . Затем они ранжируются по назначению их модулей, и если минимальное значение оказывается меньше теоретической значимости, то соответствующий коэффициент выводится из модели и все расчеты повторяются. Расчеты заканчиваются тогда, когда все коэффициенты регрессии оказываются значимыми.

Критерий согласия хи-квадрат

При обработке результатов машинного эксперимента с моделью системы часто возникает задача определения эмпирического закона распределения случайной величины. Общая схема решения этой задачи сводится к тому, что:

• строят по результатам имитационного эксперимента гистограмму (оценку функции плотности распределения вероятностей);

• выдвигают гипотезу о согласии эмпирического закона с каким-либо теоретическим распределением;

• проверяют гипотезу с помощью одного из статистических критериев согласия (Пирсона, Колмогорова, Смирнова и т.д.

В качестве критерия проверки гипотезы по критерию Пирсона выбирают величину, которая характеризует степень расхождения эмпирического и теоретического закона следующим образом: (2.5.1)

где: - количество значений случайной величины , попавших в i – ый подынтервал;

- вероятность попадания случайно величины в i – ый подынтервал;

d- количество подынтервалов, на которые разбивается интервал измерения в имитационном эксперименте, 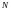- объем наблюдений.

При закон распределения величины хи-квадрат, являющейся мерой расхождения, зависит только от количества подынтервалов и приближается к закону распределения с степенями свободы, где - число параметров теоретического закона распределения. Функция распределения величины табулирована

Проверка гипотезы о согласованности эмпирического и теоретического законов распределения с помощью критерия согласия Пирсона осуществляется в последовательности:

1. Результаты наблюдений группируют в интервальный вариационный ряд. Объем наблюдений должен быть достаточно большим ( ). Если частота, соответствующая какому-либо интервалу, окажется меньше 5, то интервал объединяют с соседним, так, чтобы частота попадания значения случайной величины в подынтервал была бы больше или равна 5.

2. Выдвигают гипотезу о виде распределения по виду гистограммы.

3. Задают уровень значимости .

4. Определяют теоретическую вероятность попадания случайно величины в каждый из подинтервалов.

5. Вычисляют величину расхождения законов .

6. Определяют число степеней свободы .

7. По вычисленным значениям и по таблицам находят вероятность . Если она превышает уровень значимости , то считают, что гипотеза о виде распределения отвергается.

Определение методов решения

Для решения поставленной задачи выбран метод имитационного моделирования, так как он является наиболее оптимальным для такого типа задач. Использование языков высокого уровня, таких как С++, Delphi, Pascal, неэффективно в силу того, что реализация элементов системы с заданными свойствами (в частности, многопоточности) требует достаточно сложных синтаксических конструкций. Оптимальным в плане времени создания модели и возможности быстрой модификации является язык GPSS.

Анализ и оценка результатов моделирования производилась средствами пакета Statistica 8.0, включающего широкий спектр методов для расчета основных статистических характеристик параметров системы, построения гистограмм, реализации параметрической идентификации модели и прочих целей.