Конечные разности различных порядков.

Пусть: y =f(x) - заданная функция

- фиксированная величина приращения аргумента

Тогда - называется первой конечной разностью функции y, или конечной разностью первого порядка.

Вторая конечная разность, или конечная разность второго порядка.

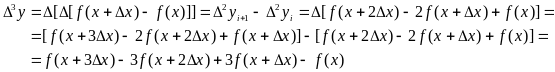
Третья конечная разность, или конечная разность третьего порядка.

Т.о., в общем виде:

Конечная разность n-го порядка.

Пример:

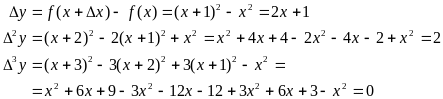
Конечные разности различных порядков удобно располагать в форме таблиц двух видов: горизонтальной и диагональной таблиц разностей

x	y
x0	y0
x1	y1
...	...	...	...	...

Диагональная таблица разностей.

x	y
X0	Y0
X1	Y1
X2	Y2
X3	Y3

Пример: горизонтальная таблица функции y = f(x) = x² при

, x₀ = 0 начальное значение, x₆=5 конечное значение

x	y
0	0	1	2	0
1	1	3	2	0
2	4	5	2	0
3	9	7	2
4	16	9
5	25

Диагональная таблица

x	y
0	0
		1
1	1		2
		3		0
2	4		2
		5
3	9

При составлении таблиц возможные ошибки вычисляются и диагональная таблица наглядно показывает нам, как отразится ошибка в значении y_n.

Следует заметить, что максимальная ошибка – в той же горизонтальной строке, где и табличная величина y_n.

Пример: исправить ошибку в таблице (неверные цифры взяты в скобки).

				Ошибка
15	13,260		0
		884
16	14,144		0
		884
17	15,912		0
		884
18	15,028		(-4)0
		88(0)4
19	16,79(2)6		(8)0
		88(8)4
20	17,680		(-4)0
		884
21	18,564		0
		884
22	19,448		0
		884
23	20,332		0

Как видно из таблицы, ход вторых разностей нарушается при x=19. Ошибка распространяется на 3 строки. Находим среднее арифметическое значение второй разности для средней из 3 точек:

= , =

Внося исправление в табличное значение y для x=19, получим верное значение функции:

_n=(y_n+ )- =16.792-(-0.004)=16.796.