Погрешность разности.

Разность двух приближённых чисел u = x₁- x₂ . Предельная абсолютная погрешность _u разности равна сумме предельных абсолютных погрешностей уменьшаемого и вычитаемого, т.е.

_ux₁+x_2.

Предельная относительная погрешность разности:

,

где А - точное значение абсолютной велечины разности чисел x₁ иx₂.

Потеря точности, если уменьшаемое и вычитаемое близки друг к другу (x₁ x₂) и имеют малые абсолютные погрешности, то число А мало, отсюда _u велико.

Пример: x₁ = 47,132;x₂ = 47,111 - пять верных цифр.

_u = 0,0005 + 0,0005 = 0,001

_x1 0,00001; _x2 0,00001 в 500 раз превышает предельную

относительную погрешность разности по сравнению с исходными данными.

В таких случаях меняют вычислительные схемы.

Погрешность произведения.

Относительная погрешность произведения нескольких приближённых чисел, отличных от нуля, не превышает суммы относительных погрешностей этих чисел.

Пусть u = x₁ · x₂ · ...· x_n.

Предположим, что числа положительны, тогда:

ln u = ln x₁ +ln x₂ + ...+ln x_n

используя приближённую формулу:

ln x d ln x = x/x исходим:

Беря выражение по абсолютной величине, получим:

т.к. точное число близко к точному, то

,

где А_i - точный сомножитель x_i

_i - относительная погрешность сомножителей x_i

• - относительная погрешность произведения

₁₂_n

Следствие: предельная относительная погрешность произведения равна сумме предельных погрешностей сомножителей, т.е.

_u_x1_x2_xn

Зная _n произведение u, можно определить его предельную абсолютную погрешность _u по формуле:

_u = |u|·_u

Пример: x₁ = 12,3; x₂ = 35,48;x₁ = 0,05; x₂ = 0,005

_u_x1_x2

т.к. произведение u = 436,404, то

_u = u·_u = 436,404·0,0041 = 1,8

Результат имеет два верных знака и результат записывают:

u = 436 2

Частный случай.

u = k · x, где k - точный множитель, отличный от нуля. Тогда:

_u = _u и _u = |k|·_x

т.е. при умножении числа на точный множитель k относительная предельная погрешность не меняется, а абсолютная предельная погрешность увеличивается в |k| раз.

Число верных знаков.

1. Если все сомножители имеют m верных знаков и число их не более 10, то число верных знаков произведения на одну или две единицы меньше m.

2. Если количество верных цифр в сомножителях различно, то число верных цифр в произведении на одну или две единицы меньше числа верных знаков в наименее точном сомножителе.

Пример: u = 93,87 · 9,236

относительная погрешность _u = ¹/₂ · (¹/₉ + ¹/₉) · ¹/₁₀₀₀ =

= ¹/₉ · 10^-3 < ¹/₂ · 10^-3,

отсюда u имеет не менее трёх верных цифр.

Погрешность частного.

Пусть U= , тогда ln u=ln x-ln y

, отсюда

Относительная погрешность частного не превышает суммы относительных погрешностей делимого и делителя. И как следствие:

Пример: Найти частное, число верных знаков в нём x=25,7; y=3,6

u =7,14 =>

В широком смысле (верные цифры те, у которых абсолютная погрешность не превышает 1) две верные цифры, а в узком - одна.

7.14 0.11

Правило определения верных знаков частного.

Если x и y имеют m верных цифр, и если и - их первые значащие цифры, то за предельную относительную погрешность частного u может быть принята величина:

Отсюда правило:

1. и 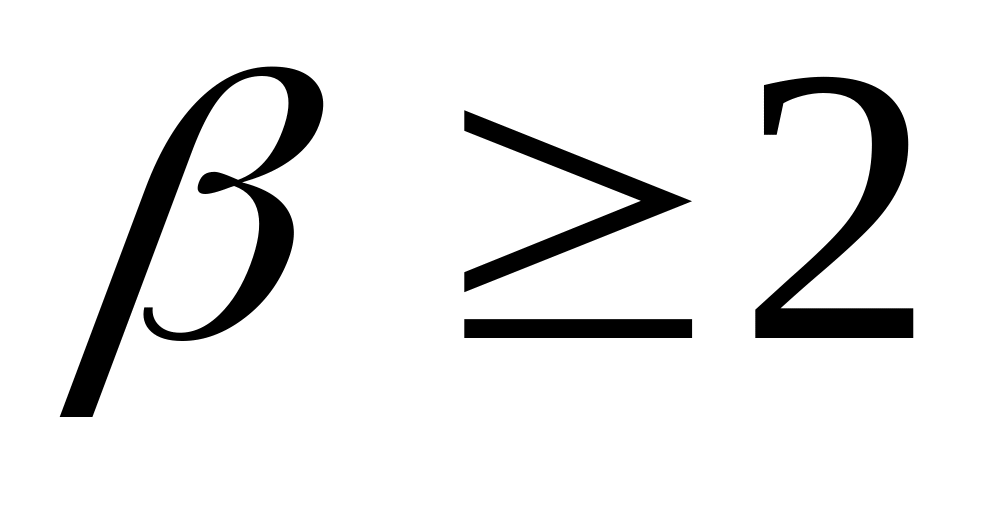, то u имеет (m-1) верных знаков;

2. или , то u имеет (m-2) верных знаков;

Относительная погрешность корня.

, отсюда , отсюда:

Предельная относительная погрешность корня m-ой степени в m раз меньше предельной относительной погрешности подкоренного числа.

Пример:

т.к.

, отсюда

число а имеет четыре верных знака (в широком смысле), отсюда

а = 3,513.

Погрешность степени.

, отсюда ln u = m ·ln x, отсюда , отсюда

.

Вычисление без точного учёта погрешности.

При массовых вычислениях, когда не учитывают погрешности каждого отдельного результата, рекомендуется пользоваться следующими правилами подсчёта цифр:

1. При сложении и вычитании младший разряд результата должен быть наибольшим десятичным размером, выражаемых верными последними цифрами исходных данных;

2. При умножении и вычитании в результате надо сохранять столько значащих цифр, сколько их имеет приближённое данное с наименьшим числом верных значащих цифр;

3. При возведении в квадрат или в куб приближённого числа в результате надо сохранять столько значащих цифр, сколько верных значащих цифр имеет основание степени;

4. При извлечении квадратного или кубического корней приближённого числа в результате надо сохранять столько значащих цифр, сколько верных цифр имеет подкоренное число;

5. Во всех промежуточных результатах следует сохранять на одну цифру больше, чем рекомендуют предыдущие правила. В окончательном результате запасная цифра отбрасывается;

6. Если берётся логарифм выражения, состоящего из приближённых чисел, то необходимо выявить число верных цифр в приближённом числе, имеющем наименьшее их число, и воспользоваться таблицей логарифмов с числом десятичных знаков, на единицу большим. В окончательном результате последние значащие цифры отбрасываются;

7. Если данные можно брать с произвольной точностью, то для получения результата с k верными цифрами исходные данные надо брать с таким числом, которое согласно предыдущим правилам обеспечивает (k+1) верную цифру в результате.