8.2. Метод э. Зибеля.
Широко известна методика, предложенная Э. Зибелем.
Исходная
квадратная ячейка делительной сетки
при однородной деформации превращается
в параллелограмм. Вписанная в исходный
квадрат окружность превращается в
эллипс (рис. 8.1). Фиксируются сопряженные
диаметры
,
соединяющие
точки касания эллипса со сторонами
параллелограмма, и угол
между ними.
Рис. 8.1. Схема преобразования окружности в эллипс по Э. Зибелю
Главные оси эллипса определяются так:
(8.1)
Угол между большой главной осью эллипса и большим сопряженным диаметром вычисляется по формуле:
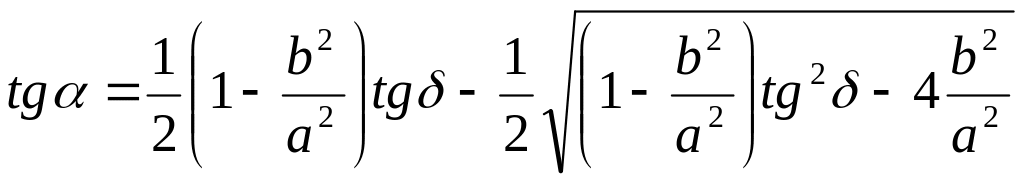(8.2)
Главные компоненты деформации находятся по уравнениям:
;
(8.3)
,
а интенсивность деформации с учетом условия несжимаемости определяется так:
(8.4)
Для выполнения расчетов удобно пользоваться координатами точек Касания A, В, С и D, а полученные характеристики формоизменения считать локальными для точки 0 в центре ячейки (рис. 8.1).
8. 3. Метод п. О. Пашкова.
Исходная квадратная ячейка делительной сетки, нанесенной в главной плоскости, превращается В параллелограмм (рис. 8.2). Система координат хОу принимается с началом в точке О — центре ячейки.
Параметрами,
отображающими искажение ячейки, как и
раньше, будут стороны параллелограмма
и
и угол между
ними δ1,
а поворот относительно фиксированных
на плоскости осей координат характеризуют
углы
и
,
причем:
.
(8.5)
Длина
и направление (угол
)
некоторого отрезка
,
имеющего до
деформации длину
и направление,
определяемое параметром п
,
значение которого по условию однородности
деформаций постоянно, используются для
определения деформации удлинения
этого отрезка:
.
(8.6)
Соответственно определяется:
.
(8.7)
Рис. 8.2. Искажение квадратной ячейки делительной сетки
По п. О. Пашкову.
Значения параметра п, определяющие направления главных осей деформации, находятся из условия их экстремума:
(8.8)
Перед радикалом
знак (+) соответствует
,
а минус —
.
Подставляя значения и в уравнение (8.6), получим:
(8.9)
т. е. тот же результат, что и по методу Э. Зибеля — см. уравнение (8.3). Интенсивность деформированного состояния определяется по уравнению (8.4).
Расчетные формулы методов Э. Зибеля и П. О. Пашкова таковы, что исходная ячейка делительной сетки должна обязательно иметь квадратную форму. Погрешность в нанесении ортогональной сетки может, очевидно, привести к ошибке в определении, как значений главных компонентов деформаций, так и направлений главных осей.