
- •Kəsilməz və diskret modellər.
- •Xətti və qeyri-xətti modellər.
- •Və funkisyasının tapılması məsələsi əmsalın təyini tərs məsələsi adlanır.
- •Aproksimasiya 2. Dayanıqlıq 3. Yığılma
- •Ilə işarə etsək, onda belə alınar:
- •Optimal idarəetmə məsələlərinin həll üsulları
- •Verilmiş funksionalın qradiyentini hesablayaq. Bunun üçün aşağıdakı əvəzləməni aparmaqla (1) tənliyini operator şəklində yazaq:
- •İndi tutaq ki, p funksiyası aşağıdakı tənliyi ödəyir:
- •Indi əsas məsələ funksionalın ifadəsindəki birinci həddi ilə işarə etməkdir.
- •İnformasiyanı bərpa edən proqramlar.
- •If then
- •İnformasiyanı ötürən
- •İnformasiyanı qəbul edən
- •İnformasiyanı
- •İnformasiyanı
- •Imzalayan şəxs imzalma faktından boyun qaçıra bilməməlidir.
Aproksimasiya 2. Dayanıqlıq 3. Yığılma
Diskret analoqlar qurularkən alınan ifadə hökmən diferensial tənliyi və əlavə şərtləri bu və ya digər tərtibdən aproksimasiya etməlidir.
Alınan cəbri tənlıiklər sisteminin həlli dayanıqlı olmalıdır və nəhayət şəbəkə addımları 0-a yaxınlaşdırıldıqda diskret məslənin həlli diferensial məsələnin həllinə yığılmalıdır. Fərq sxemləri nəzəriyyəsində Laks teoremi adı ilə isbat edilən teoremdə birinci iki şərt ödənildikdə üçüncü şərtin də ödənildiyi isbat olunub. Başqa sözlə göstərilir ki, əgər diskret tənliklər sistemi diferensial tənliyi aproksimasiya edirsə və bu sistemin həlli dayanıqlıdırsa, onda diskret məsələnin həlli diferensial məsələnin həllinə yığılır. Indiyə qədər stasionar və qeyri-stasionar birölçülü məsələlərin mükəmməl ədədi həll üsulları işlənmişdir, lakin çoxölçülü məsələlərin həllində kifayət qədər problemlər mövcuddur. Məlumdur ki, çoxölçülü qeyri-stasionar məsələlərin ədədi həll üsulu ilk dəfə amerikalı riyaziyyatçılar-Keçford və başqaları tərəfindən tənlik həll edilmişdir. Bu üsul dəyişən istiqamətlər adlandırılmışdır. Bu üsula anoloji olaraq sovet riyaziyyatçıları Somarski, Yannenkov və s. tərəfindən üsullar təklif edilmişdir. Bütün bu üsulların əsas ideyası çoxölçülü məsələlərin həllinə gətirməkdən ibarətdir. Əvvəlcə aşağıdakı tənlikdə bu üsulun əsaslandırılmasına baxaq:
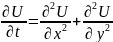

Fərz
edək ki, bu tənliyin
 anındakı həllinin tapılması məsələsinə baxaq. Bu tənliyi
operator şəklində yazaq:
anındakı həllinin tapılması məsələsinə baxaq. Bu tənliyi
operator şəklində yazaq:
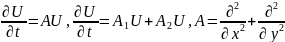
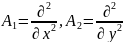
Funksiyaının Teylor sırasına ayrılışından istifadə etməklə axtarılan funksiyanın anındakı qiymətini hesablayaq:

Fərz edək ki, iki birölçülü məsələyə baxılır.


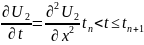
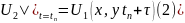
Anoloji üsulla əvvəlcə (1) və (2) məsələsinin həllərini tapaq:
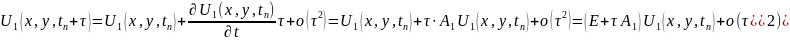
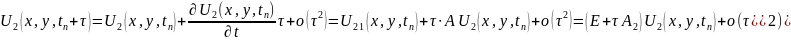
Alınan ifadədə ikinci məsələ üçün baçlanğıc şərti nəzərə alsaq, alarıq:
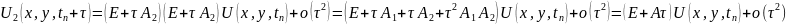
Alınan
həllin ilkin məsələylə müqayisəsi göstərir ki, bu iki həll
arasında fərq
 kəmiyyətinə bərabərdir. Buradan belə bir nəticəyə gəlmək
olar ki, verilmiş ikiölçülü məsələnin həllini tapmaq üçün
iki birölçülü məsələnin həllini tapmaq kifayətdir.
kəmiyyətinə bərabərdir. Buradan belə bir nəticəyə gəlmək
olar ki, verilmiş ikiölçülü məsələnin həllini tapmaq üçün
iki birölçülü məsələnin həllini tapmaq kifayətdir.
Ikinci
məsələdən tapılan həll ilkin məsələnin həlli qəbul edilir.
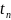 istənilən zaman anı olduğundan hesablama prosesi verilən
ardıcıllıqla davam etdirilir. Ədəbiyyatda bu üsulu
koordinatların parçalanması üsulu deyilir. (1) və (2) məsələləri
birölçülü olduğundan onların həllini tapmaq mümkündür.
Bununçün hər bir məsələnin diskret analoqunu quraq:
istənilən zaman anı olduğundan hesablama prosesi verilən
ardıcıllıqla davam etdirilir. Ədəbiyyatda bu üsulu
koordinatların parçalanması üsulu deyilir. (1) və (2) məsələləri
birölçülü olduğundan onların həllini tapmaq mümkündür.
Bununçün hər bir məsələnin diskret analoqunu quraq:

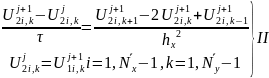
I sistemi k parametrinin qeyd olunmuş qiymətində üçdioqanallı matrisi olan xətti tənliklər sistemidir. Belə sistemin həlli Tomas alqoritmi (qovma üsulu) ilə tapılır. II system də i parametrinin qeyd olunmuş qiymətində üçdioqanallı matrisi olan xətti tənliklər sistemidir. Bu sistemin də həlli Tomas alqoritmi ilə tapıla bilər. Göründüyü kimi bir zaman layından digər zaman layına keçərkən iki birölçülü məsələnin həllini tapmaq lazım gəlir. Duqlas və digərlərinin təklif etdiyi dəyişən istiqamətlər üsulu da ikiölçülü məsələnin iki birölçülü məsələnin həllinə gətirir. Yuxarıdakı tənlik üçün bu üsul aşağıdakı şəkildə yazılır.
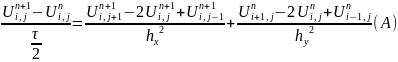

A
sxemi x dəyişəninə görə qeyri-aşkar, y dəyişəninə görə
aşkar sxemdir. Ona görə də bu sxemin tənlikləri üçdioqanalı
matrisi olan sistemin. B sxemi isə x dəyişəninə görə aşkar, y
dəyişəninə görə qeyri-aşkardır. Hər iki sistemi Tomas
alqoritmi ilə həll etmək olur. Göründüyü kimi dəyişən
istiqamətlər üsulu ilə bir zaman layından digərinə keçid iki
mərhələdə baş verir. 1-ci mrəhələdə aralıq şəbəkə
funksiyası
 tapılır. 2-ci mərhələdə isə aralıq funksiyanın
qiymətlərindən istifadə etməklə əsas həll tapılır. Lakin,
dəyişən istiqamətlər üsulunu üçölçülü məsələnin
həllinə ümumiləşdirmək olmur. Ona görə də məsələnin
ölçüsü ikidən çox olduqda koordianatlara görə və ya fiziki
proseslərə görə parçalama üsullarından istifadə edilir. Bir
sıra məsələlərin həllində isə hər iki üsulun
kombinasiyasından istifadə edilir. Aşağıdakı misalda bu
üsulların tətbiqinə baxaq:
tapılır. 2-ci mərhələdə isə aralıq funksiyanın
qiymətlərindən istifadə etməklə əsas həll tapılır. Lakin,
dəyişən istiqamətlər üsulunu üçölçülü məsələnin
həllinə ümumiləşdirmək olmur. Ona görə də məsələnin
ölçüsü ikidən çox olduqda koordianatlara görə və ya fiziki
proseslərə görə parçalama üsullarından istifadə edilir. Bir
sıra məsələlərin həllində isə hər iki üsulun
kombinasiyasından istifadə edilir. Aşağıdakı misalda bu
üsulların tətbiqinə baxaq:
Tutaq ki, qaz şəkilli tullantının atmosferdə diffuziya və küləyin vasitəsilə yayılması prosesinə baxılır. Bu prosesin riyazi modeli belə yazılır:

Küləyin sürətinin sabit olduğu qəbul edilir. Bu tənlik iki prosesin –tullantının külək vasitəsilə yayılmasını və diffuziya yolu ilə yayılmasını təsvir edir. Onda fiziki proseslərə görə parçalama üsulunun ideyasına əsasən bu tənliyi iki tənliyə parçalamaq olar.


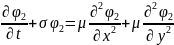

Məsələ (1) tullantının hava axını ilə yayılması prosesini təsvir edir. (2) məsələ isə tullantının diffuziya vasitəsilə yayılmasını təsvir edir. Hər iki məsələ ikiölçülüdür və bu məsələləri də koordinatlara görə parçalama üsulu ilə birölçülü məsələlərə gətirmək olar. Onda (1) məsələsinin həll sxemi aşağıdakı şəkildə yazılar:
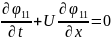


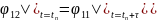
Anolji üsulla (2) tənliyini koordinatlara görə parçalayaq:
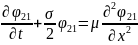
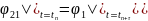
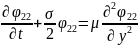

Bu sxemlərdən görünür ki, hər iki üsulun kombinasiyası son nəticədə birölçülü çəsələnin həllinə gətirilir.
18-30--Neyron şəbəkələr və onların tətbiqi
Keçən əsrin 60-cı illərindən başlayaraq modelləşdirmə problemləri ilə bağlı riyaziyyatın müxtəlif sahələrində yeni riyazi aparat təklif edilmişdir. Bu yeni sahələrə misal olaraq qeyri-səlis çoxluqlar nəzəriyyəsi, qeyri-səlis məntiq, fraktal nəzəriyyəsi, süni neyron şəbəkəsi, genetik alqoritmlər və s. Fuzzy sets nəzəriyysəi Zadə tərəfindən daxil edilmişdir. Məlumdur ki, adi çoxluq xarakteristik funksiya ilə təyin edilir. Bu o deməkdir ki, hər hansı x elementi A çoxluğuna daxildirsə,
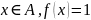

Gündəlik
həyatda elə çoxluqlara rast gəlmək olar ki, bu çoxluqların
xarakteristik funksiyası (0,1) bütün qiymətləri ala bilir.
Məsələn, yaşı 30-a yaxın olan adamların çoxluğu. Bu cür
çoxluqlara qeyri-səlis çoxluqlar və ya fuzzy sets deyilir və
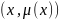 kimi təsvir edilir.
kimi təsvir edilir.
 elemenyin çoxluğa daxil olma dərəcəsidir. 770-ci illərdən
başlayaraq süni neyron şəbəkəsi sürətlə inkişaf etdirilməyə
başlamışdır. Bu nəzəriyyənin inkişafı süni intellektin
yaradılması ilə bağlıdır. (süni intellekt-qarşıya qoyulan
məsələnin insan məntiqinə anoloji alqoritmdə həllidir ).
Məlumdur ki, insan beyni neyronlar vasitəsi ilə siqnalları qəbul
edir və ötürür. Hər bir neyron dendrit və akson adlanan
çıxıntılara malikdir. Aksonlarla dendritlərin birləşdiyi
yerlər sinapslar adlanır. Süni neyronu belə təsvir etmək olar:
elemenyin çoxluğa daxil olma dərəcəsidir. 770-ci illərdən
başlayaraq süni neyron şəbəkəsi sürətlə inkişaf etdirilməyə
başlamışdır. Bu nəzəriyyənin inkişafı süni intellektin
yaradılması ilə bağlıdır. (süni intellekt-qarşıya qoyulan
məsələnin insan məntiqinə anoloji alqoritmdə həllidir ).
Məlumdur ki, insan beyni neyronlar vasitəsi ilə siqnalları qəbul
edir və ötürür. Hər bir neyron dendrit və akson adlanan
çıxıntılara malikdir. Aksonlarla dendritlərin birləşdiyi
yerlər sinapslar adlanır. Süni neyronu belə təsvir etmək olar:

Biolji neyrondan fərqli olaraq süni neyron çox sadə bir funksiyanı yerinə yetirir. Siqnalı qəbul edir, onu çevirir və çıxış siqnalı formalaşdırır. Əgər hər bir neyrona prosessor kimi baxılsa, onda süni neyron şəbəkəsi paralel işləyən prosessorların yığımından ibarətdir. Neyron siqnalı giriş telləri, yəni dendritlər vasitəsilə qəbul edir. Lakin dendritlərin ucunda olan sinapslar qəbul edilən siqnalı gücləndirə və ya zəiflədə bilər. Girişə daxil olan siqnallarkombinə olunur və öz çevirmə funksiyası (aktivasiya funksiyası ) əsasında çıxış funksiyası formalaşdırır, aksonlar vasitəsilə ötürür. Süni neyron şəbəkəsi bioloji neyron şəbəkəsinin bir modelidir. Hər bir süni neyron şəbəkəsi giriş elementlərindən, çıxış elementlərindən və gizli elementlərdən ibarətdir. Məsələn:
B u
neyron şəbəkəsi 3 giriş elementindən, 2 qat gizli neyronlardan,
2 çıxışdan ibarətdir. Adətən, neyron şəbəkə qurularkənhər
bir neyronun sərhəd qiymətinə malik olduğu nəzərdə tutulur,
yəni neyrona daxil olan siqnal bu qiymətdən çox olduqda neyron
çıxış siqnalıformalaşdırır. Əvvəlcə bir neyron üzərində
çıxış siqnalının formalaşmasına baxaq:
u
neyron şəbəkəsi 3 giriş elementindən, 2 qat gizli neyronlardan,
2 çıxışdan ibarətdir. Adətən, neyron şəbəkə qurularkənhər
bir neyronun sərhəd qiymətinə malik olduğu nəzərdə tutulur,
yəni neyrona daxil olan siqnal bu qiymətdən çox olduqda neyron
çıxış siqnalıformalaşdırır. Əvvəlcə bir neyron üzərində
çıxış siqnalının formalaşmasına baxaq:


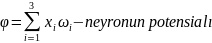
Tutaq
ki, neyronun çevirmə funksiyası f-dir. Onda
 olar. Çevirmə funksiyası süni neyron şəbəkələrdə əsasən
aşağıdakı kimi götürülür.
olar. Çevirmə funksiyası süni neyron şəbəkələrdə əsasən
aşağıdakı kimi götürülür.
Eyniyyət çevirmə funksiyası:
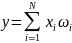
Hevisoyd funksiyası
1
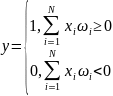
Xətti funksiya


1
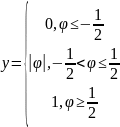
S
 iqmoid
funksiyası
iqmoid
funksiyası
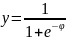
Bu funksiyanın qrafiki loqistik
funksiyanın qrafikinə oxşardır.
A

x
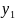

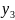
n
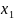

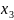
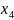
xətaları alarıq:

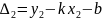


Indi isə k və b-ni elə seçmək lazımdır ki, bu xəta bu xətalar kifayət qədər kiçik olsunlar. Onda məsələ aşağıdakı funksiyanın minimumunun tapılmasından ibarət olur:

Bu üsula ən kiçik kvadratlar üsulu deyilir. Onda bu məsələnin həllini ümumi şəkildə belə yaza bilərik:
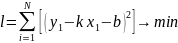
Bunun üçün verilən funksiyanın k və b-ə görə törəmələrini 0-a bərabər edirik
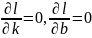
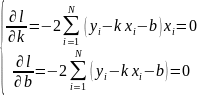

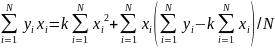

B
1
1.9
1
u məsələnin süni neyron şəbəkəsiylə həllinə keçməzdən əvvəl hər bir neyronun çıxış siqnalının necə formalaşdırdığından baxaq:

çıxış
-1
-1
o.8
1
1
1
0.5

Fərz edək ki, aktivasiya funksiyası Hevisoyd funksiyasıdır. Onda çıxış 1 olacaqdır.
F ərz
edək ki, hər hansı prosesi diaqnostika edirik. Neyronun öyrədilmə
prosesi üçün ilkin məlumatlar olmalıdır. Bu məlumatlar iki
sinfə bölünür. 1-ci sinif məlumat neyrona öyrədilir
(tanıdılır). 2-ci sinif məlumatlar isə neyronu test etmək
(yoxlamaq) üçün istifadə edilir. Əgər şəbəkə 2-ci sinif
məlumatı düzgün tanısa, onda neyron məsələnin həllinə hazır
hesab edilir. Əgər neyron şəbəkədəki əlaqə əmsallarına
ixtiyari qiymət versək, hər bir çıxış neyronunda aşağıdakı
parametrləri tapmaq olar.
ərz
edək ki, hər hansı prosesi diaqnostika edirik. Neyronun öyrədilmə
prosesi üçün ilkin məlumatlar olmalıdır. Bu məlumatlar iki
sinfə bölünür. 1-ci sinif məlumat neyrona öyrədilir
(tanıdılır). 2-ci sinif məlumatlar isə neyronu test etmək
(yoxlamaq) üçün istifadə edilir. Əgər şəbəkə 2-ci sinif
məlumatı düzgün tanısa, onda neyron məsələnin həllinə hazır
hesab edilir. Əgər neyron şəbəkədəki əlaqə əmsallarına
ixtiyari qiymət versək, hər bir çıxış neyronunda aşağıdakı
parametrləri tapmaq olar.
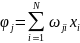

Neyron
şəbəkənin əlaqə əmsalları
 (sinaps əmsalları) təqribi seçildiyindən çıxış neyronun
formalaşdırdığı qiymət real qiymətdən fərqli olacaq, yəni
(sinaps əmsalları) təqribi seçildiyindən çıxış neyronun
formalaşdırdığı qiymət real qiymətdən fərqli olacaq, yəni

neyronun
çıxışında (*) qədər xəta olacaq.
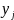 -çıxışdakı
real qiymətdir,
-çıxışdakı
real qiymətdir,
 -
çıxışda alınmalı qiymətdir. Neyrona şəbəkəni öyrətmək
əmsallarını öyrənmək deməkdir. Çıxışn xəta ilə alınması
o deməkdir ki, əlaqə əmsalları düzgün təyin edilməmişdir.
Bu əmsalları təyin etmək üçün yenə də qradiyenrt üsulundan
istifadə edilir. Bu məqsədlə aşağıdakı funksionalı qururuq:
-
çıxışda alınmalı qiymətdir. Neyrona şəbəkəni öyrətmək
əmsallarını öyrənmək deməkdir. Çıxışn xəta ilə alınması
o deməkdir ki, əlaqə əmsalları düzgün təyin edilməmişdir.
Bu əmsalları təyin etmək üçün yenə də qradiyenrt üsulundan
istifadə edilir. Bu məqsədlə aşağıdakı funksionalı qururuq:

Burada M-çıxış neyronlarının sayıdır. Qradiyent üsuluna görə verilən funksionalı minimumlaşdıran əlaqə əmsallarının qiymətləri

əmsalların artımı isə funksiyanın törəmələri ilə təyin edilir.
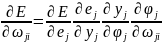
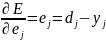

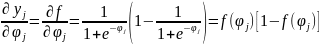
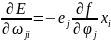
Əgər

