
- •Kəsilməz və diskret modellər.
- •Xətti və qeyri-xətti modellər.
- •Və funkisyasının tapılması məsələsi əmsalın təyini tərs məsələsi adlanır.
- •Aproksimasiya 2. Dayanıqlıq 3. Yığılma
- •Ilə işarə etsək, onda belə alınar:
- •Optimal idarəetmə məsələlərinin həll üsulları
- •Verilmiş funksionalın qradiyentini hesablayaq. Bunun üçün aşağıdakı əvəzləməni aparmaqla (1) tənliyini operator şəklində yazaq:
- •İndi tutaq ki, p funksiyası aşağıdakı tənliyi ödəyir:
- •Indi əsas məsələ funksionalın ifadəsindəki birinci həddi ilə işarə etməkdir.
- •İnformasiyanı bərpa edən proqramlar.
- •If then
- •İnformasiyanı ötürən
- •İnformasiyanı qəbul edən
- •İnformasiyanı
- •İnformasiyanı
- •Imzalayan şəxs imzalma faktından boyun qaçıra bilməməlidir.
1--Kompüter elmlərinin aktual problemləri
Keçən əsrin 50-ci illərindən başlayaraq kompüter texnologiyasının inkişafı ilə əlaqədar olaraq informatika termini daxil edilmişdir (Fransada). Bu elm sahəsi elektron hesablama maşınlarının köməyi ilə informasiyanın emalını nəzərdə tuturdu. Sonrakı dövrdə informatika informasiyanın alınması, ötürülməsi və emal edilməsi problemləri ilə məşğul olmuşdur. Lakin bu termin əvəzinə ingilis dilli ölkələrdə kompüter science və ya komputing science (kompüter haqqında elm sahəsi) terminindən istifadə olunur. Lakin hərfi tərcümədə hesablama elmləri kimi də izah edilə bilər. Müasir dövrdə kompüter elmlərinin əsas istiqaməti kimi aşağıdakı sahələrə bölünür:
Kompüterlərin arxitekturası;
Proqramlaşdırma dilləri;
Verilənlər bazası və onların idarə edilməsi;
İnformasiya çevrilməsi, emalı;
Lakin bu istiqamətlərin hər birində təkcə fundamental elm sahələri deyil praktiki məsələlər də öyrənilir. Kompüter elmlərinin daha bir interpretasiyası rus alimləri (Somarski...)tərəfindən qəbul edilmişdir. Bu interpretasiyaya görə hər hansı bir sahədə kompüter texnologiyasının tətbiqi həmin sahədə mövcud olan problemlərin modelləşdirilməsindən başlayır. Adətən modelləşdirilmə nəzərdə tutulur. Riyazi model dedikdə verilən proses və yaxud obyekti təsvir edən riyazi münasibət başa düşülür. Riyazi model ola bilər cəbri tənlik, adi diferensial tənlik, xüsusi diferensial tənlik, inteqral tənlik və s. şəklində ola bilər. Riyazi modelə prosesi xarakterizə edən əsas parametrlər daxil olur və prosesin tədqiq edilməsi bütün parametrlərin təyin edilməsini tələb edir. Lakin əksər hallarda proseslərn riyazi modelləri analitik şəkildə tədqiq oluna bilmədiyindən ədədi üsulların tətbiq edilməsi zərurəti yaranır, başqa sözlə riyazi modellərin kompüterdə realizə edilməsi zərurəti meydana çıxır. Modelin realizə edilməsi üçün əvvəlcə ədədi üsul işlənilməli, bu üsulun alqoritmi və alqoritmi realizə edən kompüter proqramı qurulmalıdır. Göründüyü kimi hər bir problemin öyrənilməsi 3 mərhələdən ibarət olur. 1-ci mərhələdə prosesin riyazi modeli qurulur, 2-ci mərhələdə modelin ədədi realizə üsulu seçilir, 3-cü mərhələdə kompüter proqramı qurulur. Müasir dövrdə kompüter elmləri ixtisası bu üçlüyü , yəni model, alqoritm, proqram əhatə edən fənləri öyrənir. Prosesləri və obyektlərin riyazi modellər əsasında öyrənilməsi rus dilli ədəbiyyatda hesablama eksprimenti aparılır. Hesablama eksprimenti əvvəllər təkcə fiziki proseslərin və ya texniki obyektlərin öyrənilməsində istifadə edilirdi. Bu üsul bu sahələrdə daha səmərələri istifadə edilir ki, fiziki modelləşdirmə mümkün olmasın ( fiziki model dedikdə baxılan prosesin kiçildilmiş və ya böyüdülmüş forması başa düşülür. Real obyektdə baş verən proses eyniliklə modeldə baş verir, məsələn, SES qurulmazdan əvvəl onun kiçildilmiş formada fiziki modeli qurulur. Model üzərində təcrübələr aparmaqla prosesin əsas göstəriciləri təyin edilir və onun əsasında real SES qurulur). Bütün obyektlərin, məsələn, AES-in fiziki modelini qurmaq mümkün deyil. Ona görən də riyazi modelləşdirmə üsullarından istifadə etmək lazım gəlir. Riyazi modelləşdirmə bütün sahələrdə, tibdə, biologoyida, ekologiyada, cihazqayırma sahəsində, layihələndirmə sahəsində və s. tətbiq edilir. Riyazi modelləşdirmə üsulu ilə obyektlərin, proseslərin öyrənilməsi birdəfəlik akt deyil. Adətən, qurulmuş model əsasında aparılan hesablamaların nəticələri real obyektdən götürülmüş verilənlərlə müqayisə edilir. Əgər modeldən alınan nəticələrlə obyektdən götürülmüş məlumatlar az fərqlənsələr, onda qurulan model adekvat hesab edilir və bu modeldən optimal rejimlərin təyin edilməsi üçün istifadə edilə bilər. Əgər model adekvat olmazsa, onda riyazi modeldə korreksiya etmək lazım gəlir. Modeldə düzəlişlər o vaxta qədər davam etdirilir ki, modeldən alınan nəticələr obyektdən alınan nəticələrlə uzlaşsın.
2-41--Proseslərin riyazi modelləşdirilməsi.
Hər hansı prosesin və ya obyektin riyazi modelinin qurulması bu prosesin sözlə təsvirindən başlayır. Yəni, proses haqqında ümumi məlumat verilir, onu xarakterizə edən əsas göstəricilər təyin edilir və nəhayət müəyyən postulatlar (hipotezlər) irəli sürülür. Postulatlar prosesi xarakterizə edən əsas parametrlər arasındakı asılılıqların xarakterini müəyyən edir və prosesin tabe olduğu fiziki qanunları müəyyən edir. Prosesin bu cür təsviri, yəni sözlə izahı təsviredici model adlanır. Məsələn, fərz edək ki, yaya bağlanmış m kütləli yükün rəqs prosesinin riyazi modelini qurmaq tələb olunur.

Bu
prosesi xarakterizə edən əsas parametrlər yayın sərtliyi (k),
cismin kütləsi (m), bu cismə təsir edən qüvvə (F) və
koordinatıdır. Fərz edək ki, cismin yerdəyişməsi zamanı
meydana çıxan elastik qüvvə yerdəyişmə ilə düz mütənasibdir.
Fizika kursundan məlumdur ki, hərəkət tənliyi kimi əksər
hallarda Nyutonun ikinci qanunundan istifadə edilir, yəni
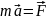 ,
ümumi halda
,
ümumi halda
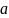 -
təcildir.
-
təcildir.
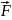 təsir edən qüvvələrin əvəzləyicisidir. Əgər cismin rəqsinin
x oxu boyunca baş verdiyini və bu zaman sürtünmə qüvvəsi çox
kiçik olduğundan, onu nəzərə almasaq, onda hərəkət tənliyi
təsir edən qüvvələrin əvəzləyicisidir. Əgər cismin rəqsinin
x oxu boyunca baş verdiyini və bu zaman sürtünmə qüvvəsi çox
kiçik olduğundan, onu nəzərə almasaq, onda hərəkət tənliyi
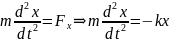
Bu tənlik sürtünmə qüvvəsi nəzərə alınmadıqda yaya bərkidilmiş cismin rəqsinin riyazi modelidir.
Göründüyü kimi riyazi model qurularkən prosesi xarakterizə edən əsas parametrləri və onların arasındakı qanunauyğunluqların təyin edilməsi çox mühüm məsələdir. Öyrənilən proses haqqında informasiya almaq üçün prosesi təsvir edən riyazi model tədqiq edilməlidir. Məsələn, yuxarıdakı prosesin riyazi modeli ikinci tərtib sabit əmsallı adi diferensial tənlikdən ibarətdir. Bu tənliyi həll etməklə rəqs edən cismin koordinatının zamandan asılılığını tapmaq olar. Eylerə görə bu tənliyin həlli aşağıdakı şəkildə axtarılır:
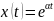


Alınan tənliyə diferensial tənliyin xarakteristik həlli deyilir
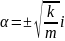
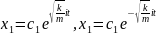
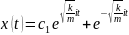
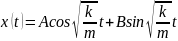
A
və B sabitlərdir. Alınan ifadə göstərir ki, baxılan cisim
harmonik rəqs edir və bu rəqsin periodu
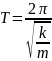
Lakin qeyd etmək lazımdır ki, bu model baxılan harmonik rəqsin periodunu
(tezliyini) tapmağa imkan verir, lakin bu model əsasında rəqsin amplitudunu təyin etmək mümkün olmur. Rəqsin amplitudunu təyin etmək üçün əlavə şərtlər verilməlidir, adətən, bu şərtlərə başlanğıc şərtlər deyilir (başlanğıc zaman anında cismin koordinatı və sürəti məlum olmalıdır). Qurulan modeldə daha bir çatışmazlıq var ki, real rəqs prosesləri həmişə sönən olur, lakin bu modelə görə rəqs prosesi sönmür. Ona görə modelin real rəqs prosesini təsvir etməsi üçün sürtünmə qüvvəsinin cismin sürətinə mütənasib olduğunu qəbul etsək, onda yuxarıdakı model

Burada
 -
sürtünmə qüvvəsinin təsirini nəzərə alır. Bu misal bir daha
göstərir ki, hər hansı prosesin riyazi modeli qurularkən
modelləşdirmənin məqsədi dəqiqləşdirilməlidir, çünki,
qarşıya qoyulan məqsəddən asılı olaraq eyni bir proses üçün
müxtəlif modellər qurmaq olar.
Ümumiyyətlə riyazi modellərə qoyulan ümumi tələbləri
aşağıdakı şəkildə ifadə etmək olar:
-
sürtünmə qüvvəsinin təsirini nəzərə alır. Bu misal bir daha
göstərir ki, hər hansı prosesin riyazi modeli qurularkən
modelləşdirmənin məqsədi dəqiqləşdirilməlidir, çünki,
qarşıya qoyulan məqsəddən asılı olaraq eyni bir proses üçün
müxtəlif modellər qurmaq olar.
Ümumiyyətlə riyazi modellərə qoyulan ümumi tələbləri
aşağıdakı şəkildə ifadə etmək olar:
Modelin adekvatlığı-hər şeydən əvvəl qurulan model baxılan prosesə keyfiyyətcə adekvat olmalıdır. Bu o deməkdir ki, modeldən təyin edilən parametrlərin dəyişmə tendensiyası real prosesdəki tendensiyaya uyğun olmalıdır. Əsasən, bioloji, sosioloji proseslərin modelləşdirilməsində qurulan modellərin keyfiyyətcə adekvat olması kifayət etmir. Model həm də kəmiyyət baxımından adekvat olmalıdır. Yəni modeldən tapılan parametrlərin qiymətləri prosesdən alınan qiymətlərə uyğyn olmalıdır. Məsələn, yuxarıda baxılan prosesin riyazi modeli harmonik rəqsin tezliyinin təyin edilməsi baxımından adekvat sayıla bilər. Lakin sürtünmə qüvvəsinin təsiri nəzərə alınmadığından digər xarakteristikaların təyin edilməsi zamanı model adekvat olmayacaqdır.
Model tam olmalıdır. Bu o deməkdir ki, prosesi xarakterizə edən ən mühüm parametrlər modeldə nəzər alınmalıdır və model qarşıya qoyulan məqsədi təyin etməyə imkan verməlidir. Məsələn, yuxarıdakı model rəqsin amplitudunu təyin etməyə imkaç vermədiyindən tam ola bilməz.
Model robastlıq(möhkəm) xassəsinə malik olmalıdır.


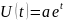
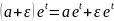
Göründüyü
kimi başlanğıc verilən
 xəta ilə verilirsə, onda həll
xəta ilə verilirsə, onda həll
 olur, deməli, model robastlıq xassəsinə malik deyil. Əgər
modelə daxil olan parametrlərin ilkin qiymətləri kiçik
dəyişdikdə modeldən alınan nəticələr də kiçik dəyişirsə,
onda model robastlıq xassəsinə malik sayılır, əks halda model
robast deyil.
olur, deməli, model robastlıq xassəsinə malik deyil. Əgər
modelə daxil olan parametrlərin ilkin qiymətləri kiçik
dəyişdikdə modeldən alınan nəticələr də kiçik dəyişirsə,
onda model robastlıq xassəsinə malik sayılır, əks halda model
robast deyil.
26--Riyazi modellərin tipləri
Adətən riyazi modellər onların strukturuna, modelə daxil olan dəyişənlərin formasından asılı olaraq aşağıdakı tiplərə bölünür:
Struktur və funksional modellər.
Əgər riyazi model prosesin və ya obyektin ayrı-ayrı elementləri, hissələri arasındakı əlaqəni, tabe olunan qanunauyğunluğu əks etdirirsə, belə model struktur model adlanır. Başqa sözlə struktur modeldə prosesin daxili quruluşu öz əksini tapır. Məsələn, istilikkeçirmə, diffuziya proseslərinin modelləri struktur modellərdir. Lakin elə modellərə rast gəlinir ki, bu modellərdə prosesin strukturu, daxili əlaqələr nəzərə alınmır. Model yalnız prosesə təsir edən xarici amillərlə (prosesin girişi ilə) çıxış arasındakı əlaqəni xarakterizə edir. Belə modellərə qara qutu da deyilir. Bu halda modelin qurulması girişlə çıxış arasındakı hər hansı asılılığın qurulmasından ibarət olur.
Kəsilməz və diskret modellər.
Məlum olduğu kimi kəmiyyətlər kəsilməz və diskret olmaqla iki qrupa bölünür. Kəsilməz kəmiyyət elə kəmiyyətə deyilir ki, o verilmiş aralıqda istənilən qiyməti ala bilir. Diskret kəmiyyət isə verilmiş aralıqda ayrı-ayrı qiymətlər ala bilir. Analoji olaraq modelə daxil olan kəmiyyətlərin tiplərindən asılı olaraq riyazi modellər kəsilməz və diskret olurlar. Lakin bu böəgü şərti xarakter daşıyır. Kəsilməz modeldən diskret modelə və əksinə həmişə keçmək mümkün olur. Məsələn, istilikkeçirmə tənliyi
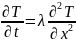
Bircins mühitdə istiliyin yayılması prosesini təsvir edir və kəsilməz modeldir. Əgər tənliyə daxil olan törəmələri aproksimasiya etsək,
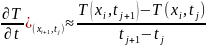

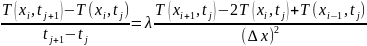
diskret modelini alarıq. Bəzən ola bilər ki, eyni bir modeldə diskret və kəsilməz dəyişənlər iştirak etsin.
Xətti və qeyri-xətti modellər.
Məlumdur
ki, ixtiyari x və y dəyişənləri arasında xətti asılılıq
mövcuddursa, onda bu asılılıq
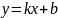 şəklində yazıla bilər. Bu dəyişənlərin artımları arasında
da xətti asılılıq mövcud olur :
şəklində yazıla bilər. Bu dəyişənlərin artımları arasında
da xətti asılılıq mövcud olur :
 . Əgər y iki dəyişəndən asılıdırsa, onda anoloji olaraq
. Əgər y iki dəyişəndən asılıdırsa, onda anoloji olaraq
 asılılıqlarını yazmaq olar. Fizika kursunda məlmumdur ki,
çoxsaylı fiziki kəmiyyətlər arasında xətti asılılıq
mövcuddur. Məsələn, Huk qanunu
asılılıqlarını yazmaq olar. Fizika kursunda məlmumdur ki,
çoxsaylı fiziki kəmiyyətlər arasında xətti asılılıq
mövcuddur. Məsələn, Huk qanunu

Om qanunu

Furye qanunu

Bu fiziki qanunları çox vaxt səbəblə nəticə arasındakı əlaqə şəklində qəbul edirlər. Əgər səbəb və nəticə arasındakı əlaqə xətti funksiya şəklində ifadə edilirsə, onda alınan model xətti, əks halda qeyri-xətti hesab edilir. Ümumiyyətlə xətti modellər xətti cəbri diferensial tənliklərlə ifadə edilir. Məsələn, yuxarıda göstərilən istilikkeçirmə tənliyi xətti modeldir.
Determinik və stoxastik(güman edilən) modellər.
Əgər riyazi modelə statistik göstəriciləri məlum hesab edilən hər hansı təsadüfi faktor daxil olarsa, belə model stoxastik hesab edilir (təsadüfi faktor-təsadüfi funksiya, kəmiyyət). Əgər modeldə təsadüfi faktor iştirak etmirsə, onda model determinik hesab edilir.
Statik və dinamik modellər.
Bəzən aralıq modellər kimi kvazi statik, stasionar və kvazi stasionar modelləri fərqləndirirlər. Statik modelə görə təsvir edilən proses və ya obyekt zamana görə dəyişmir. Dinamik modelə görə isə obyektin parametrləri zamana görə dəyişir.
2--Bəzi proseslərin riyazi modellərinin qurulması
Proseslərin riyazi modellərinin qurulma mexanizmini başa düşmək üçün bəzi proseslərin riyazi modelinin qurulmasına baxaq:
Fərz edək ki, qaz şəkilli maddələrin (müəssisələrin tullantılarının) atmosferdə yayılması prosesinə baxılır. Aşkardır ki, bu maddələrin atmosferdə yayılması prosesi iki yolla baş verir: küləyin vasitəsilə, konveksiya və diffuziya yolu ilə.
Bu
prosesin riyazi modelini qurmaq üçün onu xarakterizə edən əsas
parametrləri müəyyən etmək lazımdır. Bu parametrlər kimi
tullantının konsentrasiyası
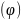 (vahid həcmə düşən kütlə) götürülür. Küləyin sürət
vektorunu
(vahid həcmə düşən kütlə) götürülür. Küləyin sürət
vektorunu
 qəbul edək. Yuxarıda qeyd edildiyi kimi prosesin riyazi modelini
qurmaq üçün elementar həcm təsəvvür edək :
qəbul edək. Yuxarıda qeyd edildiyi kimi prosesin riyazi modelini
qurmaq üçün elementar həcm təsəvvür edək :
Tilləri
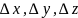 olan düzbucaqlı paralepiped şəklində götürülmüş elementar
həcm üçün fizikanın fundamental qanununu- kütlənin saxlanması
qanununu yazaq. Bu qanuna görə
olan düzbucaqlı paralepiped şəklində götürülmüş elementar
həcm üçün fizikanın fundamental qanununu- kütlənin saxlanması
qanununu yazaq. Bu qanuna görə
 m
m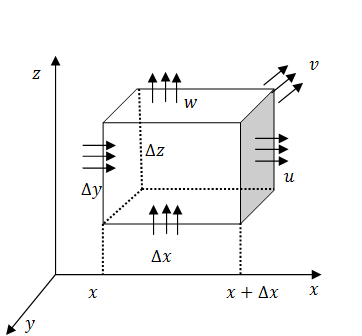 üddətində
bu həcmə daxil olan tullantının kütləsi ilə
üddətində
bu həcmə daxil olan tullantının kütləsi ilə
bu həcmdən xaric olan kütlənin fərqi bu həcmdəki kütlənin artımına bərabrədir.

Əvvəlcə müddətində bu həcmdə daxil olan kütləni hesablayaq:

Analoji üsulla müddətində bu həcmdən xaric olan kütləni hesablamaq olar:
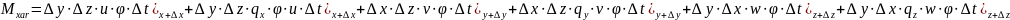
Verilən həcmdəki kütlə artımını aşağıdakı şəkildə təyin etmək olar:
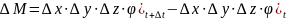
Bu ifadələri kütlənin saxlanması qanununda yerinə yazaq

Alınan
tənliyin hər iki tərəfini
 -ə
bölək:
-ə
bölək:

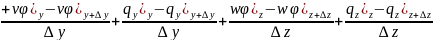
A lınan
tənlikdə limitə keçsək,
lınan
tənlikdə limitə keçsək,

Işarə olunmuş hədlər diffuziyanın təsirini xarakterizə edir. Bu hədləri ekspriment əsasında təyin etmək mümkün olmur. Ona görə də empirik düsturlardan istifadə edilir. Diffuziya prosesində bu empirik düstur Fik qanunu ilə ifadə edilir.
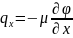
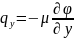

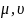 diffuziya
əmsalları adlanır. Bu ifadələri nəzərə alsaq, onda yuxarıdakı
tənlik aşağıdakı şəkildə yazılar:
diffuziya
əmsalları adlanır. Bu ifadələri nəzərə alsaq, onda yuxarıdakı
tənlik aşağıdakı şəkildə yazılar:

tullantının atmosferdə yayılması prosesinin riyazi modelidir
8--Birölçülü stasionar məsələnin analitik həllinin qurulması
Ümumi halda istilikkeçirmə prosesi üçölçülü elliptik tip tənliklərlə təsvir edilir. Bu tənliyin analitik həllini xüsusi hallarda qurmaq mümkün olur. Birölçülü halda bu tənliyin analitik həllinin qurulmasına baxaq:
Fərz
edək ki, istilik yalnız x oxu istiqamətində yayılır və ətraf
mühitlə istilik mübadiləsi baş verir. X oxunun ixtiyari
 nöqtəsində vahid zaman ərzində Q qədər istilik verilir. Onda
bu prosesin riyazi modelini
nöqtəsində vahid zaman ərzində Q qədər istilik verilir. Onda
bu prosesin riyazi modelini

şəklində yaza bilərik. Istiliyin yayıldığı mühitin bircins olduğu nəzərdə tutulur. Bu ikinci tərtib adi diferensial tənlikdir. Bu tənlik üçün iki sərhəd şərti verilməlidir. Bu şərtləri belə yazaq:
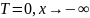
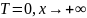
Baxılan
tənlikdə
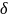 funksiya iştirak etdiyinə görə, onun bu şəkildə analitik həll
etmək mümkün olmur. Ona görə
funksiyanın xassəsindən istifadə etməklə bu tənliyi iki
tənliyə parçalamaq olur. Məlumdur ki,
funksiya iştirak etdiyinə görə, onun bu şəkildə analitik həll
etmək mümkün olmur. Ona görə
funksiyanın xassəsindən istifadə etməklə bu tənliyi iki
tənliyə parçalamaq olur. Məlumdur ki,
 funksiyası
nöqtəsindən başqa bütün nöqtələrdə 0-a bərabərdir. Onda
nöqtəsindən sol tərəfdə bu tənlik
funksiyası
nöqtəsindən başqa bütün nöqtələrdə 0-a bərabərdir. Onda
nöqtəsindən sol tərəfdə bu tənlik

Anoloji olaraq nöqtəsindən sağ tərəfdə tənlik

olar. I tənliyin həllini tapaq:



Onda I məsələnin həlli belə yazılır:

burada
 və
və
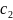 naməlum sabitlərdir. Alınan funksiya I məsələdəki sərhəd
şərtini ödəməlidir. Bu o zaman mümkün olar ki,
naməlum sabitlərdir. Alınan funksiya I məsələdəki sərhəd
şərtini ödəməlidir. Bu o zaman mümkün olar ki,
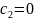 olsun. Onda I
məsələsinin həlli
olsun. Onda I
məsələsinin həlli
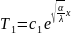
olar. Anoloji üsulla II məsələnin həllini tapa bilərik.
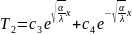
Bu
həll verilən sərhəd şərtini o zaman ödəmiş olar ki,
 olsun. Nəticədə
olsun. Nəticədə
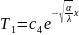
Göründüyü
kimi verilmiş məsələnin həlli iki naməlum
və
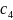 sabitlərindən ibarət oldu. Bu sabitləri təyin etmək üçün iki
əlavə şərt verilməlidir. Bu şərtlərdən biri temperaturun
bütün nöqtələrdə kəsilməz olmasından alınır.
sabitlərindən ibarət oldu. Bu sabitləri təyin etmək üçün iki
əlavə şərt verilməlidir. Bu şərtlərdən biri temperaturun
bütün nöqtələrdə kəsilməz olmasından alınır.
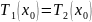
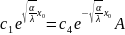
2-ci
şərti almaq üçün ilk verilən tənliyi
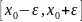 parşasında
inteqrallayaq
parşasında
inteqrallayaq

funksiyanın xassəsinə görə

Onda hissə-hissə inteqrallama düsturunu tətbiq etsək alarıq:

 olduqda
olduqda
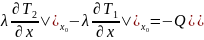

A
və B-dən
 -ü
tapaq
-ü
tapaq
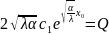


Beləliklə, qurulan məsələnin analitik həlli aşağıdakı üsulla tapılır:
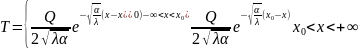

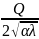

35--Riyazi modellərin identifikasiyası
Müasir dövrə riyazi modelləşdirmə obyektlərin öyrənilməsi üsullarından biridir. Riyazi model qurularkən əsas problemlərdən biri məqsədin düzgün təyin edilməsidir. Yəni, modelləşdirmədən hansı xarakteristikanın öyrənilməsi dəqiq məlum olmalıdır. Çox vaxt ədəbiyyatda riyazi modelin qurulması və əsaslandırılması identifikasiya adlanır. Identifikasiya iki qrupa bölünür. Struktur və parametrik identifikasiya.
Struktur identifikasiya dedikdə riyazi modelinin strukturunun təyin edilməsi başa düşülür. bu sahədə ümumi bir üsul yoxdur. Bir çox hallarda modelin strukturu evristik üsullarla təyin edilir. Adətən riyzi modelləri strukturuna görə iki qrupa bölürlər: toplanmış və paylanmış parametrli modellər.
Əgər riyazi model adi diferensial tənliklə təsvir edilirsə, belə model toplanmış parametrli model sayılır. Əgər model xüsusi törəməli diferensial tənliklə təsvir edilirsə, o paylanmış parametrli model sayılır ( axtarılan funksiya fəza koordinatlarından da asılı olur). Riyazi modelin strukturu müəyyən edildikdən sonra modelə daxil olan parametrlərin təyin edilməsi məsələsi ortaya çıxır. Parametrlərin təyin edilməsi məsələsi parametrik identifikasiya məsələsi adlanır. Struktur və parametrik identifikasiya məsələləri tərs məsələlər sinfinə daxildir. Ümumiyyətlə riyazi fizika məsələlərini düz və tərs olmaqla iki qrupa bölürlər. Əgər riyzi model səbəb və nəticə arasındakı əlaqəni təsvir edirsə, onda düz məsələ verilən səbəbə görə nəticəni tapmaqdan ibarət olur. Alınmış nəticəyə görə səbəbin müəyyən edilməsi məsələsi tərs məsələdir. Texniki diaqnostika, tibbi diaqnnostika məsələləri tərs məsələlərdir. Əgər riyazi nöqteyi nəzərdən düz məsələyə baxılırsa, bu zaman riyazi modelə daxil olan əmsalların başlanğıc şərtlərinin, sərhəd şərtlərinin məlum olduğu fərz edilir.
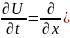
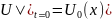
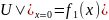

Qoyulmuş
məsələdə k(x), f(x,t),
 ,
,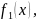
 funksiyaları məlum olarsa (səbənlər),
funksiyaları məlum olarsa (səbənlər),
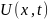 funksiyiasının tapılması düz məsələdir. Əgər göstərilən
səbəblərdən hər hansı biri məlum olmazsa və onun tapılması
tələb olunarsa, bu tərs məsələ sayılır.
Bir
çox ədəbiyyatda tərs məsələləri 4 qrupa bölürlər
(adətən rus dilli ədəbiyyatda), bəzi ədəbiyyatlarda isə 5
qrupa bölürlər.
funksiyiasının tapılması düz məsələdir. Əgər göstərilən
səbəblərdən hər hansı biri məlum olmazsa və onun tapılması
tələb olunarsa, bu tərs məsələ sayılır.
Bir
çox ədəbiyyatda tərs məsələləri 4 qrupa bölürlər
(adətən rus dilli ədəbiyyatda), bəzi ədəbiyyatlarda isə 5
qrupa bölürlər.
Retrospektiv (zamanı geri qaytarmaq)
Sərhəd tərs məsələlər
Əmsalın təyini tərs məsələləri
Həndəsi tərs məsələ
Bu tərs məsələlər qeyri-korrekt məsələlər sinfinə daxildir. Bu termini ilk dəfə fransız riyaziyyatçısı Adamar daxil etmişdir. Ümumiyyətlə riyazi fiziki məsələlər o zaman korrekt sayılır ki,
Məsələnin həlli olsun
Bu həll yeganə olsun
Həll ilkin verilənlərdən kəsilməz asılı olsun
İlk dəfə Adamar qeyri-korrekt məsələyə misal qurmuşdur. O göstərmişdir ki, Laplas tənliyi üçün Koşi məsələsi qeyri-korrektdir.
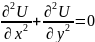
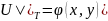

32--Retrospektiv tərs məsələ.
Retrospektiv tərs məsələ aşağıdakı şəkildə qoyulur.


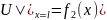
Bu məsələnin qeyri-korrekt olduğunu göstərmək üçün sadə məsələyə baxaq:




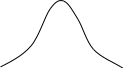
Məsələni həll etmək üçün Furye üsulundan istifadə edək. Furye üsuluna görə verilən məsələnin həlli

Əgər bu həlli verilən tənlikdə yerinə yazsaq
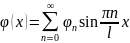

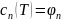

Burada
 inteqrallama
sabitidir. Başlanğıc şərti nəzərə alsaq, onda
inteqrallama
sabitidir. Başlanğıc şərti nəzərə alsaq, onda
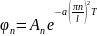


Fərz edək ki, bu əmsalın t=0-dakı qoymətini tapmaq tələb olunur.
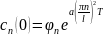
Adətən
riyazi fizika məsələlərində ilkin verilənlər ölçmə
nəticəsində alınır və özündə xəta saxlayır. Fərz edək
ki,
 kəmiyyətləri də
kəmiyyətləri də
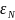 xətası ilə hesablanmışdır. Hər bir
xətası ilə hesablanmışdır. Hər bir
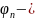 in
əvəzinə
in
əvəzinə
 hesablanır. Əgər bu iadəni düsturda yerinə yazsaq, alarıq:
hesablanır. Əgər bu iadəni düsturda yerinə yazsaq, alarıq:
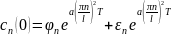
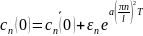
Alınan
ifadədən göründüyü kimi
əmsalı çox kiçik
 xətası
ilə verilərsə
xətası
ilə verilərsə
 ifadəsi çox böyük xəta ilə tapılır. Bu isə o deməkdir ki,
retrospektiv tərs məsələnin həlli ilk verilənlərdən kəsilməz
asılı deyil. Korrekt olmanın 3-cü şərtinə əsasən bu məsələ
qeyri-korrektdir.
ifadəsi çox böyük xəta ilə tapılır. Bu isə o deməkdir ki,
retrospektiv tərs məsələnin həlli ilk verilənlərdən kəsilməz
asılı deyil. Korrekt olmanın 3-cü şərtinə əsasən bu məsələ
qeyri-korrektdir.
Sərhəd tərs məsələsi.
Tutaq ki, bu prosesin riyazi modeli aşağıdakı şəkildədir:

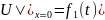
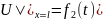
Tutaq
ki,
 funksiyası məlum deyil və bu funksiyanın tapılması tələb
olunur.aydındır ki, məsələnin korrekt olması üçün
funksiyası məlum deyil və bu funksiyanın tapılması tələb
olunur.aydındır ki, məsələnin korrekt olması üçün
 funksiyasının əvəzinə başqa şərt verilməlidir. Tutaq ki,
baxılan oblastın hər hansı
funksiyasının əvəzinə başqa şərt verilməlidir. Tutaq ki,
baxılan oblastın hər hansı
 nöqtəsində ölçmə aparmaq mümkündür. Onda əlavə şərti
nöqtəsində ölçmə aparmaq mümkündür. Onda əlavə şərti
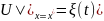
şəklində
yaza bilərik. Beləliklə,
 məlum olduqda,
və
funksiyasının tapılması sərhəd tərs məsələsi adlanır. Bu
da qeyri-korrekt məsələdir.
məlum olduqda,
və
funksiyasının tapılması sərhəd tərs məsələsi adlanır. Bu
da qeyri-korrekt məsələdir.
Əmsalın təyini tərs məsələsi.
Tutaq ki, prosesin riyazi modeli aşağıdakı şəkildədir:
Fərz
edək ki, k(x) funksiyası naməlumdur və onun tapılması tələb
olunur. lakin , bu şərtlər məsələnin həllini tapmağa kifayət
etmir. əlavə şərtlər verilməlidir. Tutaq ki, əlavə şərtlər
kimi
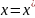 nöqtəsində ölçmə aparılır. Yəni
nöqtəsində ölçmə aparılır. Yəni

