2.2. Примеры решения задач

Пример 1. Определить количество вещества и число молекул, содержащихся в 1г углекислого газа.

Р

Дано:

m = 1 г = 110^3 кг

 = 44

10^3 кг/моль

 = ? N = ?

ешение:

Количество вещества:

.

Число молекул:

.

Ответ: В одном грамме углекислого газа содержится 2,2710^2 молей вещества и 1,410²² молекул.

Пример 2. В баллоне объемом V = 25 л находится водород при температуре Т = 290 К. После того как часть водорода израсходовали, давление в баллоне понизилось на р= 0,4МПа. Определить массу израсходованного водорода.

Р

Дано:

V = 25 л = 2510^3 м³

 = 210^3 кг/моль

Т = 290 К = const

р = 0,4 МПа =0,410⁶ Па

m = ?

ешение:

Масса израсходованного водорода:

,

где m₁, m₂ – масса водорода в начальном и конечном состояниях.

Из уравнения Менделеева-Клапейрона найдем массу водорода в начальном и конечном состояниях:

.

Тогда

.

Проверим размерность полученной формулы:

Делаем расчет:

Ответ: Было израсходовано 8,3 грамма водорода.

Пример 3. Количество =1кмоль многоатомного газа нагревается на Т=100 К в условиях свободного расширения. Найти количество теплоты Q, сообщенное газу, приращение его внутренней энергии U и работу А, совершаемую газом при расширении.

Дано:

 = 1 кмоль = 110³ моль

i = 6

Т = 100 К

р = const 

Q = ? U = ? А = ?

Решение:

Количество теплоты, сообщенное газу при изобарном нагревании найдем по формуле:

,

где  молярная теплоемкость газа при постоянном давлении, i – число степеней свободы молекулы. Исходя из этого

.

Вычисляя, получим Q=33,2410⁵ Дж 3,3210⁶ Дж =3,32 МДж.

Приращение внутренней энергии газа

, где 

молярная теплоемкость газа при постоянном объеме. Тогда

.

После вычислений: U = 2,49 МДж.

Согласно первому закону термодинамики: .

Вычисляя, получим А = 0,83 МДж.

Ответ: Количество теплоты, сообщенное газу Q=3,32МДж; приращение его внутренней энергии U=2,49МДж; работа, совершенная газом А = 0,83 МДж.

Пример 4. Тепловая машина, работающая по циклу Карно, за цикл получает от нагревателя количество теплоты Q_1=2,5кДж. Температура нагревателя Т₁ = 400 К, температура холодильника Т₂ = 300 К. Найти работу А, совершаемую за один цикл и количество теплоты Q₂, отдаваемое холодильнику за один цикл.

Р

Дано:

Q₁ = 2,5 кДж

Т₁ = 400 К

Т₂ = 300 К 

А = ? Q₂ = ?

ешение:

Термический КПД идеальной тепловой машины

,

где Т₁ – температура нагревателя, Т₂ – температура холодильника.

С другой стороны ,

где А – работа, совершаемая газом за один цикл, Q₁ – количество теплоты, полученное от нагревателя; откуда

.

Вычисляя, получим: А = 0,625 кДж.

Известно, что работа, совершаемая за один цикл ,

тогда

.

Вычисляя, получим Q₂ = 1,875 кДж.

Ответ: Работа, совершаемая за один цикл А = 0,625 кДж; количество теплоты, отдаваемое холодильнику за один цикл Q_2=1,875 кДж.

3. Электростатика.

Постоянный электрический ток

3.1. Перечень формул, которые можно использовать

при решении задач без вывода

Закон Кулона (сила F взаимодействия двух точечных неподвижных зарядов Q₁ и Q₂)

,

где e - относительная диэлектрическая проницаемость среды; – электрическая постоянная; r – расстояние между зарядами.

Линейная t и поверхностная s плотности заряда

Напряженность электрического поля:

а) через величину пробного заряда q, внесенного в электрическое поле

где – сила, действующая на пробный заряд;

б) созданного точечным зарядом Q на расстоянии r от него

в) образованного бесконечной прямой равномерно заряженной нитью на расстоянии r от нее

,

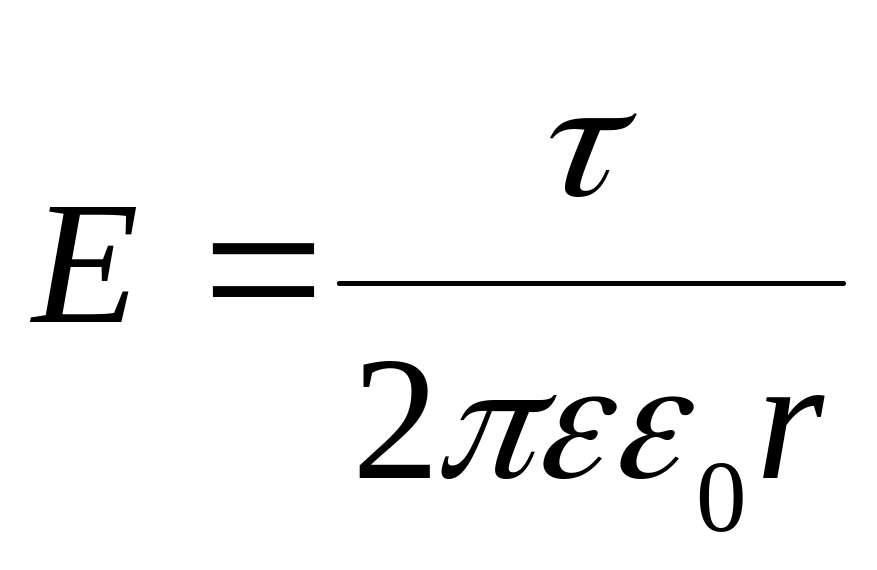где t - линейная плотность заряда на нити;

г) образованного бесконечной равномерно заряженной плоскостью

,

где s - поверхностная плотность заряда;

д) образованного разноименно заряженными параллельными бесконечными плоскостями (поле плоского конденсатора)

;

е) образованного заряженной сферой радиуса R

где r – расстояние от центра сферы .

Связь между напряженностью электрического поля и электрической индукцией

.

Теорема Гаусса (поток Ф_Е вектора напряженности электрического поля через замкнутую поверхность S, охватывающую точечные заряды Q_i)

Потенциал электрического поля

,

где W_n – потенциальная энергия пробного заряда q, внесенного в это поле.

Потенциал электрического поля, созданного точечным зарядом Q

.

Напряженность и потенциал поля, создаваемого проводящей заряженной сферой радиусом R на расстоянии r от центра сферы

а) Е = 0, (при r < R);

б) , (при r = R);

в) , (при r > R),

где Q – заряд сферы.

Напряженность и потенциал поля, создаваемые системой точечных зарядов (принцип суперпозиции электрических полей):

, ,

где , - напряженность и потенциал в данной точке электрического поля, создаваемого зарядом.

Связь потенциала j с напряженностью :

а) или в общем случае;

б) в случае однородного поля;

в) в случае поля, обладающего центральной или осевой симметрией.

Напряженность и потенциал электрического поля, создаваемого распределенными зарядами:

,

,

где - единичный вектор, направленный из точки, где находится заряд dQ, в рассматриваемую точку поля.

Работа перемещения заряда q в электрическом поле

.

Энергия W взаимодействия системы точечных зарядов Q₁, Q₂, …, Q_n

здесь j_i – потенциал поля, создаваемого всеми (n-1) зарядами (за исключением i–ого), где расположен заряд Q_i.

Электрический момент диполя

,

где - плечо диполя (векторная величина, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами).

Электрическая емкость уединенного проводника и конденсатора:

, ,

где Q – заряд, сообщенный проводнику (пластине конденсатора); j - потенциал проводника; – разность потенциалов пластин конденсатора.

Электрическая емкость:

а) уединенной проводящей сферы радиуса R

;

б) плоского конденсатора

,

где S – площадь одной пластины; d – расстояние между пластинами.

Энергия уединенного заряженного проводника:

,

где C – емкость проводника; j - потенциал проводника (j_¥ = 0).

Энергия заряженного конденсатора

,

где U – разность потенциалов на обкладках конденсатора.

Электроемкость системы конденсаторов:

а) при параллельном соединении

или ;

б) при последовательном соединении

или .

Сила и плотность электрического тока

, ,

где dQ – заряд, прошедший через конечное сечение проводника за время dt; dS – элемент площади поперечного сечения проводника.

Сопротивление R и проводимость G проводника

, ,

где r -удельное сопротивление; l –длина проводника; g - удельная проводимость; S – площадь поперечного сечения.

Сопротивление системы проводников:

а) - при последовательном соединении;

б) - при параллельном соединении,

где R_i – сопротивление i – ого проводника.

Закон Ома:

а) - для участка цепи, не содержащего ЭДС, где j₁-j₂ =U – разность потенциалов на концах участка цепи; R – сопротивление участка цепи;

б) - для участка цепи, содержащего ЭДС, где e - ЭДС источника тока; R_полн – полное сопротивление участка (сумма внешних и внутренних сопротивлений);

в) для замкнутой (полной) цепи, где R – внешнее сопротивление цепи; r – внутреннее сопротивление цепи.

Законы Кирхгофа:

а) - первый закон;

б) - второй закон,

где - алгебраическая сумма сил токов, сходящихся в узле; алгебраическая сумма произведений сил токов на сопротивления участков; алгебраическая сумма ЭДС.

Закон Джоуля – Ленца (количество теплоты Q, выделившееся на сопротивлении R за время t при прохождении через него электрического тока):

.

Полная мощность, развиваемая источником постоянного тока

.

Полезная мощность P_R, выделяемая на внешнем сопротивлении R

.

КПД источника тока

.