2. Розв‘язання

Подія А₁ – пошкодження трансформатора яка можлива у двох випадках.

Подія В₁ – пошкодження трансформатора у решту часу.

Подія В₂ – пошкодження трансформатора у період заземленої фази.

Використовуючи формулу для повної ймовірності, маємо:

- імовірність роботи трансформатора з заземленою фазою.

- імовірність нормальної роботи.

Імовірність безвідмовної роботи P(t) - це ймовірність того, що в заданому інтервалі часу t у виробу не виникає відмова.

Функція P(t) являється монотонно спадною функцією, тобто в процесі експлуатації і зберігання надійність тільки зменшується. Для визначення P(t) використовують наступну статистичну оцінку:

; де N - кількість виробів, які установлені на випробовування (в експлуатацію). N₀ - кількість виробів, що відмовили на протязі часу t.

Інтенсивність відмов - це відносна густина ймовірності появи відмови невідновлюваного об'єкту, визначеного та розглянутого моменту часу, за умови, що до цього моменту відмова не виникала. Для визначення використовують наступну статистичну оцінку:

де - кількість виробів, що відмовила за період часу .

− середня кількість справних виробів у період часу t.

Середній час напрацювання на відмову (середній час безвідмовної роботи) Т− це математичне сподівання напрацювання до першої відмови, яке визначаєтсья:

3. Загальна кількість зафіксованих відхилень 200, отже, запишемо ряд статистичних ймовірностей.

Мі	23	25	27	26	22	28 "	25	24
Рі	0,115	0,125	0,135	0,13	0,11	0,14	0.125	0,12

де n − загальна кількість відхилень.

Математичне сподівання обчислюється, як сума добутку середнього значення X, наприклад -3,5, на відповідну статистичну ймовірність, тобто:

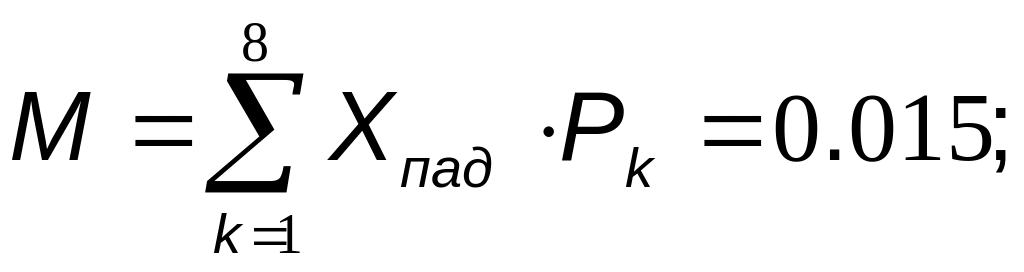
Дисперсія обчислюється як сума добутку квадрата різниці середнього значення та математичного сподівання на відповідну ймовірність, тобто:

Таким чином, стандартне відхилення по модулю

1. Показники ремонтопридатності:

Імовірність відновлення S(t) − це ймовірність того, що виріб, який відмовив, буде відновлено протягом часу t.

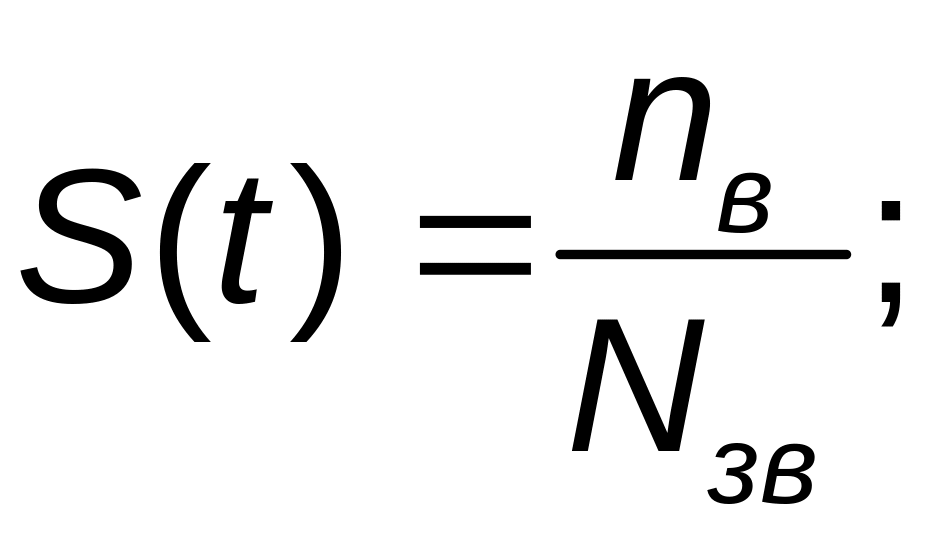де − кількість виробів, час відновлення яких було менше заданого часу t.

− кількість виробів, що залишились відновлюватись.

Інтенсивність відновлення μ(t) − відносна густина розповсюдження часу відновлення для моменту часу t за умови, що до цього моменту відновлення виробу не відбулося.

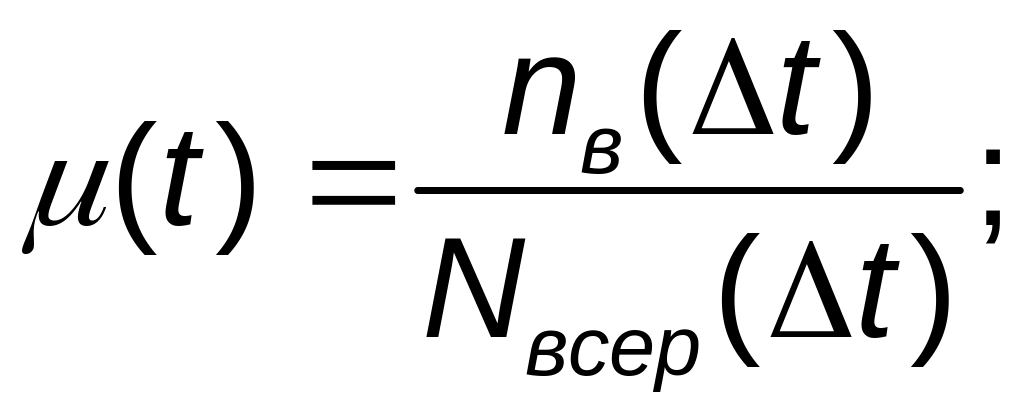
де − кількість відновлених виробів за час .

− середня кількість виробів, які не були відновлені протягом часу .

Середній час відновлення Т_в − це натуральна величина сподівання відновлення.

або

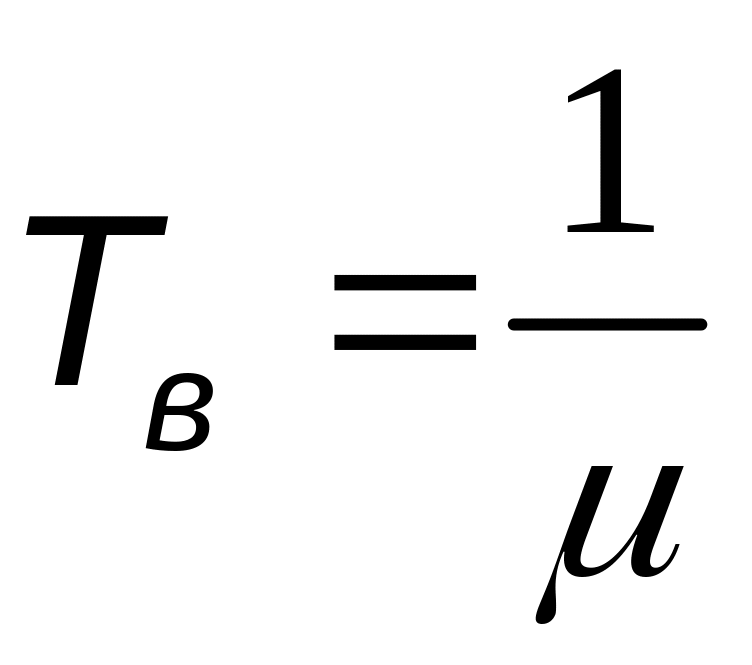
Статистична оцінка: .

2.

Розв‘язання

Період осінньо-зимового максимуму навантаженя охоплює чотири місяці, приблизно по 30 днів кожен. Отже, період годин.

Величина втраченої електроенергії за аварії буде рівна:

Відповідь: математичне сподівання не відпущеної із шин еелктростанції електроенергії 17.28 МВт ·год.

Дерево відмов – це логічна, графологічна та ієрархічна схема, яка показує зв‘язок відмов системи з відмовами елементів. Вершинами дерева є операції типа “і” та “або” (”і” – це множення подій, “або” – сума подій). Дерево відмов починається з кінцевої події, під якою вважається повна відмова системи. На більш низькому рівні позначається подія, яка викликає кінцеву подію у відповідності з логічною операцією, що зв‘язує ці події. На самому низькому рівні розташовані події відмов елементів.

Розглянемо спрощену технологічну схему енергоблока і відповідне дерево відмов.

1.Котел

2.Турбіна

3,4,5. Конденсатні насоси

6. Деаєратор

7,8. Живильні насоси

Аналіз дерева відмов заключаєтсья у визначенні такої комбінації елементів, одночасна відмова яких приведе до вершини дерева відмов енергоблока. Таким чином, функціональну схему енергоблока можна уявити як сукупність елементів, які мають послідовне і паралельне з‘єднання елементів.

При паралельному з‘єднанню елементів мається на увазі, що є резервування, наприклад, живильні насоси і конденсатні насоси.

Математичну модель дерева відмов можна уявити у вигляді:

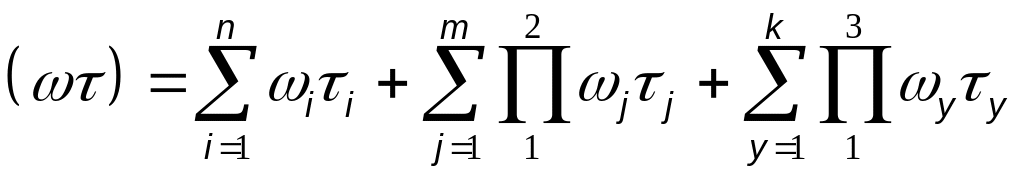
де n – кількість послідовно з‘днаних елементів (1,2,6)

m – кількість елементів з одиничним резервуванням

k – кількість елементів з подвійним резервуванням.

Імовірність відмови у цьому випадку визначається:

Коефіцієнт простою енергоблока

Коефіцієнт гототвності енергоблока

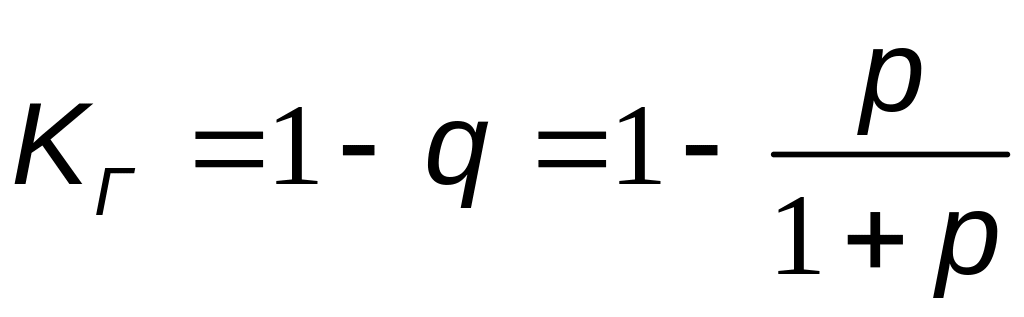
Модель дерева відмов записується відносно розрахункового елемента схеми. У даному випадку – відносно турбогенератора.

2. Схема за міщення по надійності

Еквівалентуємо елементи послідовного з‘єднання:

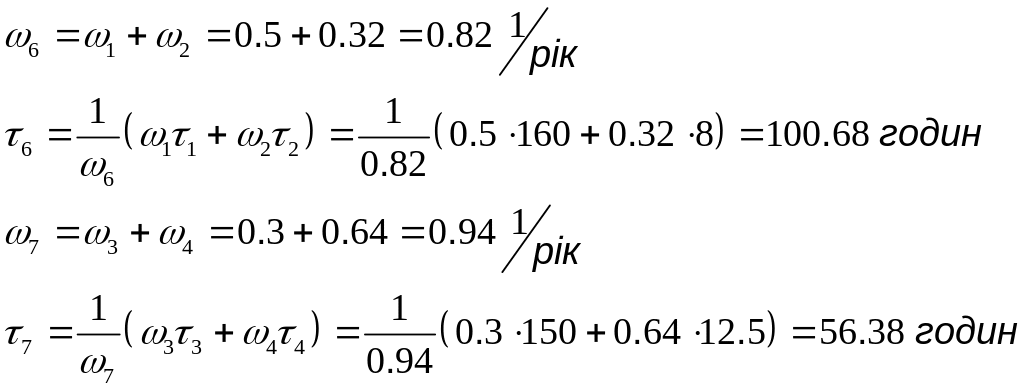
Визначаємо еквівалентний елемент 8, як паралельне з‘єднання елементів.

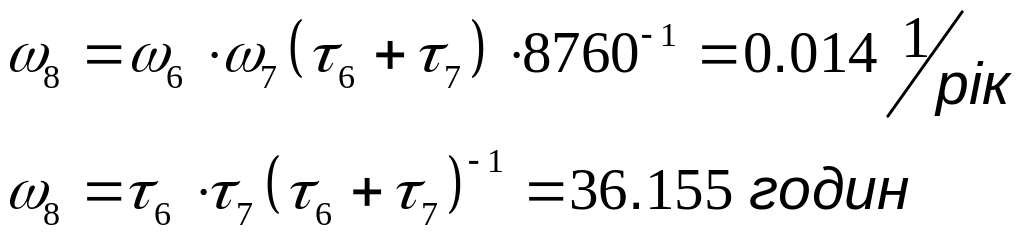
Визначаємо результуючі показники надійності блока:

Середній час безвідмовної роботи:

Коефіцієнт готовності:

Відповідь:

1. Схему неблочної електростанції з трьома секціями генераторної напруги представимо схемою заміщення по надійності.

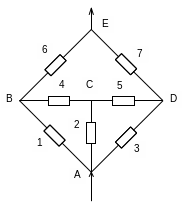
2. Складаємо матрицю безпосередніх зв‘язків вершин − ребер структури:

А 1 2 3

В 1 4 6

C 2 4 5

D 3 5 7

E 6 7

3. Складаємо масив N- дерев послідовним приєднанням до N_i – дерева вершин безпосередньо пов‘язаних з одною з вершин попереднього дерева N_i-1.

A AB AC AD ABC ACD ABD ABCD

4. Для кожного дерева знаходимо перерізи. Пошук перерізів проводимо в табличній формі.

N – дерево	А	АВ	АС	AD	ABC	ABD	ACD	ABCD
ребра	123	123 146	123 245	123 357	123 146 245	123 146 357	123 146 357	123 146 245 357
перерізи	123	2346	1345	1257	356	24567	147	67

Ребра, які входять в сукупність N_і – дерева кратне число разів – викреслюються, ті що залишилися переносяться до строки “перерізи”.

5. Вибираються мінімальні перерізи із множини отриманих. Перевіряєтьтся не вміщує переріз з більшим числом елементів переріз з меншим числом елементів. Так, переріз 24567 вміщує переріз з 67. Тому переріз24567 виключається. Всі залишившися перерізи є мінімальними.

2. Розв 'язання

Використовуючи теорему про суму ймовірностей для даного випадку маємо:

Р(А + В + С) = Р(А) + Р{В) + Р{С) - Р(АВ) - Р(АС) - Р{ВС) + Р(АВС).

Подія А - відмова першого трансформатора.

Подія В - відмова усіх паралельних ліній електропередачі.

Подія С - відмова другого трансформатора.

Подія А+В+С - припинення енергопостачання споживачів із-за вище приведених випадків.

Отже:

Відповідь: надійність 0.9987

1. Показники структурної надійності в першу чергу визначаються для окремих вузлів ( груп вузлів) об'єкту, показники функціональної надійності - для системи в цілому.

Необхідним етапом розрахунку показників структурної надійності складних систем є визначення мінімальних шляхів і перерізів схеми щодо вузлів (вузла) навантаження. Застосування принципу вимушеного перетину максимально незалежних шляхів створює не тільки можливість визначення перерізів обмеженого порядку, але і дозволяє здійснювати декомпозицію складних структур по надійності функціонування щодо вузлів навантаження.

Декомпозиція по структурі є основною цілеспрямованих заходів для зміни рівня надійності складних об'єктів.

Структурна надійність, обумовлена структурою об'єкту, тобто складом елементів і зв'язками між ними, без урахування режимних особливостей функціонування елементів.

Оцінка показників структурної надійності найбільш актуальна і має великі логічні підстави в проектній постановці завдання. При експлуатації, особливо систем з малою режимною надмірністю, домінуючого значення набуває функціональна надійність, коли до складової параметра потоку відмов елементів, обумовленою несприятливою дією зовнішніх випадкових чинників, додається складова, обумовлена відключеннями елементів при різних станах системи внаслідок неприпустимих режимів роботи.

Показники структурної надійності має сенс визначати для окремих вузлів (груп вузлів), тобто для окремих частин енергооб'єктів. Цим і визнаються склад показників надійності: ймовірність безвідмовної роботи, ймовірність відмови, параметр потоку відмов, напрацювання до відмови із заданою ймовірністю її не перевищення, тобто одиничних показників надійності об'єктів, що складаються з відновлюваних елементів. В окремих випадках знаходяться комплексні показники: недовідпуск електроенергії і питомий збиток. З урахуванням особливостей побудови енергооб'єктів показники надійності слід співвідносити до повної відмови працездатності, тобто повній втраті живлення вузла навантаження.

Для більшої частини практичних завдань оцінки надійності, зокрема в проектній практиці, немає необхідності розглядати показники надійності на нетривалих інтервалах, тому можна не враховувати початкові стани елементів.

В розрахунках структурної надійності можна використовувати прості ймовірнісні методи, засновані на середній ймовірності стану елементів: стаціонарному коефіцієнті готовності (середній ймовірності безвідмовного стану), стаціонарному коефіцієнті вимушеного простою (середній ймовірності стану відмови) і середньому значенні параметра потоку відмов (частоті відмов). Застосування їх забезпечує необхідну точність при розрахунках на тривалих інтервалах при дотриманні двох основних умов:

1) відмови елементів системи незалежні і потік відмов ординарний, тобто виключаються з розгляду відмови елементів системи внаслідок дії загальних для всіх елементів несприятливих чинників, на які не розраховані конструкції елементів;

2) час безвідмовної робота в багато разів більше часу відновлення елементів. Навіть якщо закони розподілу часу безвідмовної роботи і часу відновлення значно

відрізняються від показового, похибка розрахунку по середнім значенням незначна (до 15-20%).

2 . Складаємо матрицю безпосередніх зв‘язків вершин – ребер структури.

А 1 2 3

В 1 4 6

C 2 4 5 7

D 3 5 8

E 6 7 8

Складаємо масив N- дерев структури:

А АВ АС АD ABC ACD ABD ABCD

Для кожного дерева знаходимо перерізи в табличній формі.

N – дерево	А	АВ	АС	AD	ABC	ABD	ACD	ABCD
ребра	123	123 146	123 2457	123 358	123 146 2457	123 146 358	123 2457 388	123 146 2457 358
перерізи	123	2346	13457	1258	3567	24568	3478	678

Мінімальні перерізи розглянутої структури: 123, 678, 2346, 1258, 3567, 3478, 13457, 24568.