3.3. Жалпы жағдайда орналасқан кесiндiнiң өлшемiн және проекциялар жазықтығына көлбеу бұрышын анықтау

Бip проекциялар жазықтығына тік бұрыштап проекциялағанда кесіндінің өлшемін анықтағанбыз. Бір катеті проекцияның ұзындығына тең екінші катеті кесіндіні шектеу нүктелерінің проекция жазықтығынан қашықтықтарының алымына тең тік бұрышты үшбұрыштың гипотенузасына тең. Ал гипотенузасымен проекцияның арасындағы бұрыш сол проекциялар жазықтығымен кесіндінің арасындағы бұрыш. Горизонталь проекциялар жазықтығымен кесіндінің арасындағы бұрышты φ - әрпімен белгілейміз (21-сурет).

21-сурет

Фронталь проекциялар жазықтығымен арасындагы бұрыш - ρ, ал профиль проекциялар жазықтығымен арасындағы бұрыш δ әрпімен белгіленеді. Бұл әдісті тік бұрышты үшбұрыш әдісі деді.

Eкiншіci әдіс - Монж әдісі. Бұл әдістің айырмашылығы үшбұрыштың тұрғызуында. Екінші катет орнында қалады да, салынған горизонталь сызық бойынша тік бұрыштан бастап бірінші катетін /проекцияның/ өлшемін белгілейді (22-сурет).

Пайда болған үшбұрыш өткен үшбұрышпен бірдей тек артық орын талап етпейді. Горизонталь проекциялар жазықтығына көлбеулік бұрыш фронталь проекциялар жазьқтығына салынған үшбұрыштан табылады, ал фронталь проекциялар жазықтығына көлбеулік бұрыш горизонталь проекциялар жазықтығына салынған үшбұрышта табылады.

Жазықтық

Түзу сызықтық беттерге жазықтықта жатады.

Кеңістіктe жазықтықтың белгілі анықтауыштары: бip түзу бойында жатпайтын үш нүкте; бip нүкте және ол арқылы өтпейтін түзу; параллель немесе қиылысатын екі түзулер; жазық фигуралар /үшбұрыш, параллелограмм, көпбұрыш т.б/ (23-сурет).

Эпюрде жазықтық, анықтауыштарының проекцияларымен және іздерімен беріледі.

Жазықтықтың iзі деп оның проекциялар жазықтығымен қиылысу түзуін атайды. α- жазықтығымен фронталь / ₂ / проекциялар жазықтығымен қиылысу түзуін фронталь ізi деп, горизонталь / ₁ / проекциялар жазықтығымен қиылысу түзуiн горизонталь ізі деп және профиль / ₃ / проекциялар жазықтығымен қиылысу түзуiн профиль ізі деп атайды. Егер жалпы жағдай жазықтығы болса іздері былай белгіленеді: ; ; 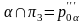(24-сурет).

Екі іздің бір осьте қиылысу нүктесін іздердің түйілісу нүктесі деп атайды және осьтермен аттас X_α,Y_α,Z _α - деп белгілейді.

Жазықтьқта жататын түзудің іздері жазьқтықтың іздерінде жатады. l - түзудің фронталь ізi ; 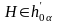(24-сурет, б).

Сондықтан жазықтьқтың iздepiн салу үшiн жазықгықта жатқан екі түзудің iздepiн тауып, олардың аттас іздерін қосса, жазықтықтың іздері пайда болады.

Кеңістікте кездесетін жазықтықтарды екі топқа бөлуге болады: жалпы жағдай және дербес жағдай орналасқан жазықтықтарға. Бip де бip проекциялар жазықтығына параллель емес жазықтықтарды жалпы жағдай жазықтықтары деп атайды.

Дербес жағдай жазықтықтар тағы eкi топқа бөлінеді: проекциялаушы және деңгейлік жазықтықтар.

Блок1

Сұрақ 3 Қисық сызықтар мен беттер. Классификация. Беттегі нүктелер және сызықтар.

Сызба геометрия сызьқты кеңістікте үздіксіз қозғалатын нүктенің проекциясы ретінде қарастырады. Үздіксіз қозғалатын нүктенің кеңістіктегі орындарының жиыны қисық сызықты анықтайды. Қисық сызықты қысқаша сызық деуге болады.

5 9-сурет

Сызықтың екі немесе бірнеше нүктелері арқылы жүргізілген түзуді қиюшы дейді. Сол нүктелер түзу бойымен бip - бipiнe шекciз жақындағанда қиюшының шегін жанама дейді. Эпюрде киюшы жанама болып проекцияланады (59-сурет, а,б).

Сызықтарды жазық және кеңiс сызықтар деп екі топка бөледі.

Жазық сызықтардың нүктелерінің бәpi жазықтықта жатады. Кеңіс сызықтардың нүктелері бip жазықтықта жатпайды.

Эллипс, шеңбер, гипербола, парабола, синусоида сияқты қисық сызықтар жазық сызықтарға жатады. Кеңіс сызықтардың ішінде техникада көп қолданалатын винттік сызықтар.

Цилиндрлік винттік сызық деп өзара параллель екі түзудің біреуі арқылы бірқалыпты айналып екіншісі бойымен бірқалыпты қозғалатын нүктенің проекциясын атайды. Бip айналғандағы қозғалуының ұзындығын адымы деп атайды. Цилиндрлік винттік сызықты салу үшін биіктігі адымына /h/ тең цилиндр алалық. Цилиндрдің горизонталь проекциясы болатын шеңберді тең 12 бөлікке бөліп, фронталь проекциясын горизонталь түзулермен тең 12 бөлікке бөліп, шеңбердің бөліну нүктелері арқылы вертикаль түзулер жүргізіледі. Бipiншi нүктеден X - ociнe дейін болса, екіншісінен бірінші горизонталь түзуге дейін, үшіншісінен - екінші горизонталь түзуге дейін,..., n- ніншісінен n+1- ісіне дейін белгілесек цилиндрлік винттік сызықтың горизонталь проекциясы шеңбер, ал фронталь проекциясы синусында болатынын көреміз. Егер нүкте осьтен айналған кезде төменнен жоғары қозғалып солдан оңға айналса винттік сызықты оңқай дейді, ал оңнан солға айналса солақай дейді (60-сурет, а,б).

Конустік винттік сызық деп өзімен қиылысатын түзуден бipқалыпты айналатын түзудің бойымен бірқалыпты қозғалатын нүктенің траекториясын айтады.

60-сурет

Конустың табанын тең 12 бөлікке бөлiп, оның жасаушыларын жүргізіп, биіктігінде тең 12 бөлікке бөліп, конустың бетінде жататын шеңберлер жүргіземіз. Нүкте жасаушы боймен ұзындығының бөлігіне қозғалғанда кезекші шеңбер бойынша оның бөлігінe айналып отырады (60-сурет, б).

Конустық винттік сызықтың фронталь проекциясы амплитудасы кемімелі синусоида, ал горизонталь проекциясы Архимед спиралі болатынын көреміз.

Сызықтың ұзындығын жуықтап салу әдісін қарастырайық. Берілген сызығының А және В нүктелерінің арасындағы бөлігінің ұзьндығын алсақ (61-сурет).

Көршілес нүктелердің аралығындағы сызықтың бөлігін кесінді ретінде қарастыруға болатындай етіп А мен В нүктелері аралығынан бipнешe нүктелерін /1, 2, 3,... / аламыз. Абсцисса осіне параллель түзу жүргізіп оған .... кесінділер салынады = /2'3'/… А "… В"- нүктелep арқылы горизонталь, - нүктелер арқылы вертикаль түзулер жүргізіп пайда болған нүктелерді 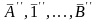белгілейміз. Кез-келген түзу жүргізіп оған /А₀1₀/, /1₀-2₀/,/2₀-3₀/…..кесінділерді саламыз./ А₀1₀/= ; /1₀-2₀/=/12/; А₀ В₀ кесінді АВ-ұзындығы. /А₀ В₀/= /А В/.

Қисық сызықты беттер

Беттер кеңістікте үздіксіз қозғалатын сызықтың траекториясымен беріледі. Траектория дегеніміз қозғалып отырған сызықтың орындарының жинағы. Бетті анықтайтын шарттарды беттің анықтауышы дейді. Беттің анықтауышы - жасаушы сызьқ және бағыттаушылар (62-сурет).

Егер бағыттаушы 6ipеy ғана болса, кез келген нүктеде жасаушы сызық бағыттаушы бойымен жылжып отырып кенеттен бағыттаушы арқылы айналып кетсе беттің тұтастығы бұзылады. Сондьқтан бағыттаушы бірнешеу болуға тиіс, кемінде екеу.

Бағыттаушылар геометриялық белгімен немесе бipeyi алгоритмдік белгімен берілуі мүмкін.

Анықтауыштардың түpiнe қарай беттерде өзгеріп отырады.

Жасаушы түзу сызық болса пайда болған беттерді түзу сызық беттері дейді. Егер түзу сызық беттерді бүкпей және үзбей жазып, жазықтықпен беттестіруге болса оларды жазылатын беттер деп атаймыз. Жазылатын беттерге цилиндрлік және конустік беттер жатады.

1 блок