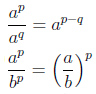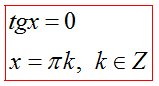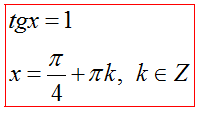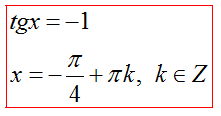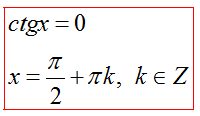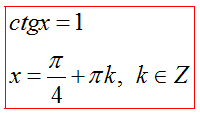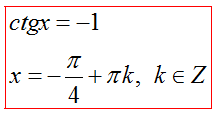1. Целые числа(Z)-это все натуральные числа и числа противоположные им по знаку, а так же число ноль.

Рациональные числа(Q)-это числа представляемые обыкновенной дробью вида m/n, где числитель m-целое число, а знаменатель n-натуральное число.

Действительные числа(R)-Множество всех рациональных и иррациональных чисел. Так же это любые положительные, отрицательные числа и ноль.

2. Приближенные вычисления-вычисления производимые с допустимой погрешностью.

Разница между точным числом x и его приближенным значением a называется погрешностью

Если  | x - a | < D_a, то величина D_a называется абсолютной погрешностью.

Отношение D_a / a = d_a называется относительной погрешностью.

Округление-операция. Позволяющая уменьшить количество знаков в числе за счет замены числа его приближенном значением с определенной погрешностью.

3. Степенью называется выражение вида: 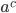 , где:

 — основание степени;

 — показатель степени.

Степень с натуральным показателем:

1. По определению:  .

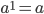2. Возвести число в квадрат — значит умножить его само на себя: 

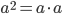
3. Возвести число в куб — значит умножить его само на себя три раза:  .

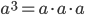Возвести число в натуральную степень   — значит умножить число само на себя   раз.

Степень с целым показателем:

Если показателем степени является целое положительное число:

, n > 0

Возведение в нулевую степень:

, a ≠ 0

Если показателем степени является целое отрицательное число:

, a ≠ 0

Степень с рациональным показателем:

Если:

• a > 0;

• n — натуральное число;

• m — целое число;

Тогда:

Свойства:

Произведение степеней
Деление степеней
Возведение степени в степень

Арифметический квадратный корень   — это неотрицательное число, квадрат которого равен 

Корень n-ой степени:

Корень n-ой степени из числа a-это число, n-я степень которого равна а

Свойства:

4. Степень с рациональным показателем:

Степенью числа a>0 с рациональным показателем  ,  где m - целое число, а n - натуральное ( n>1), называется число 

Свойства степени с рациональным показателем:

5. Логарифм по основанию a от аргумента x — это степень, в которую надо возвести число a, чтобы получить число x.

Основное логарифмическое тождество:

логарифмом числа   по основанию   называется показатель степени, в которую нужно возвести основание  , чтобы получить число  .

Десятичный логарифм, это логарифм по основанию 10. Его обозначение: lg a

Натуральный логарифм:

Логарифм, взятый по основанию e, носит название — натуральный логарифм. Его обозначение: ln a

6. Правила действий с логарифмами:

1)

2)

3)    - логарифм произведения.

Логарифм произведения равен сумме логарифмов сомножителей.

4)    - логарифм частного.

Логарифм частного (дроби) равен разности логарифмов сомножителей.

5)    - логарифм степени.

Логарифм степени равен произведению показателя степени на логарифм ее основание

6.    - логарифм степени.

Логарифм степени равен произведению показателя степени на логарифм ее основания.

7.

Переход к новому основанию по формуле:

  

Для доказания этой формулы можно воспользоваться основным логарифмическим тождеством.

7. У́гол — геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (которая называется вершиной угла)

Углом в 1 радиан называется Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности.

Градусная мера угла в 1 радиан равна:

Так как дуга длиной πR (полуокружность), стягивает центральный угол в 180°, то дуга длиной R, стягивает угол в π раз меньший, т.е.

синус угла х-Это отношение противолежащего катета к гипотенузе:

sinx = а/с

косинус угла х- Это отношение прилежащего катета к гипотенузе:

сosx= в/с

тангенс угла х- Это отношение противолежащего катета к прилежащему:

tgx = а/в

котангенс угла х- Это отношение прилежащего катета к противолежащему:

ctgx = в/а

8. Основные тригонометрические тождества:

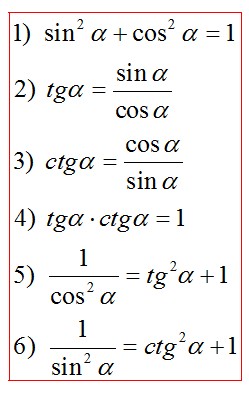
Формулы приведения:

Это соотношения, с помощью которых значения тригонометрических функций аргументов   и др., выражаются через значения  .

Правила преобразования: 1) Если аргумент содержит  , где n-нечетное натуральное число , то функция меняется на "конфункцию", т.е. синус на косинус, тангенс на котангенс и наоборот. Если n - четное натуральное число , то название функции не изменяется. 2) Определяем знак ("+" или "-") значения первоначальной функции. Преобразованное выражение сохраняет знак своего родителя

9)Формулы сложения и вычитания

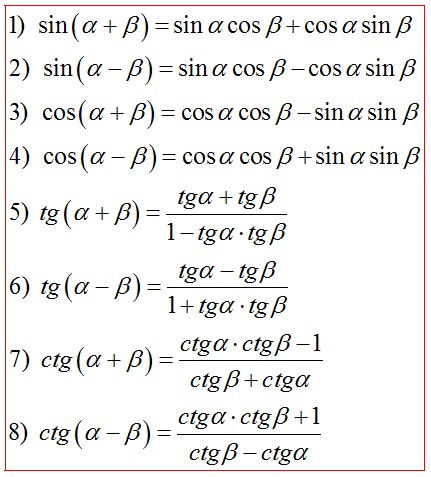
10)Формулы двойного угла:

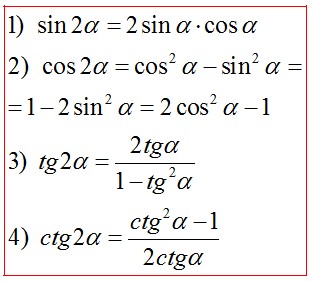
11)Формулы половинного угла:

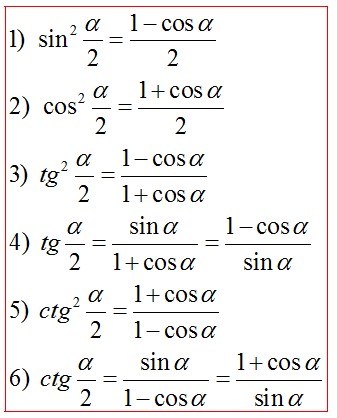
12)Арксинус

Если есть выражение sinx=a, то x=arcsina. То есть арксинусом числа а называется такое число x , что его синус равен а.

Ограничения: 

Арккосинус

Если есть выражение cosx=a, то x=arccosa. То есть арккосинусом числа а называется такое число x , что его косинус равен а.

Ограничения: 

Арктангенс

Если есть выражение tgx=a, то x=arctga. То есть арктангенсом числа а называется такое число x , что его тангенс равен а.

Ограничения: 

Арккотангенс

Если есть выражение сtgx=a, то x=arсctga. То есть арккотангенсом числа а называется такое число x , что его котангенс равен а.

Ограничения: 

Простейшие тригонометрические уравнения и их решение:

Решение уравнения sinx=a

Частные случаи:

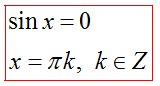
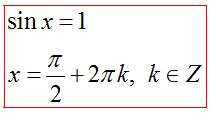
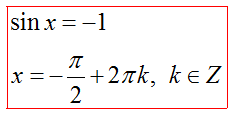
Решение уравнения cosx=a

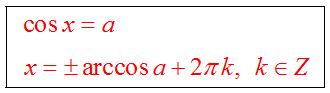
Частные случаи:

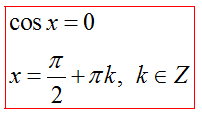
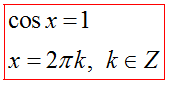
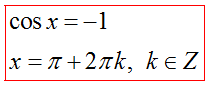
Решение уравнения tgx=a, ctgx=a

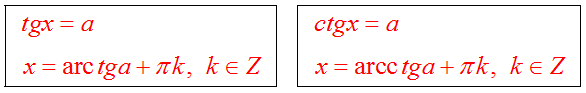
Частные случаи для tgx=a

Частные случаи для ctgx=a

13)Простейшие тригонометрические неравенства:

К простейшим тригонометрически неравенствам относятся следующие 16 неравенств:  sin x > a,     sin x ≥ a,     sin x < a,     sin x ≤ a,  cos x > a,     cos x ≥ a,     cos x < a,     cos x ≤ a,  tan x > a,     tan x ≥ a,     tan x < a,     tan x ≤ a,  cot x > a,     cot x ≥ a,     cot x < a,     cot x ≤ a.  Здесь x является неизвестной переменной, a может быть любым действительным числом.

Их решение:

  Неравенство sin x > a

3. При a ≥ 1 неравенство sin x > a не имеет решений:  x ∈ ∅

4. При a < −1 решением неравенства sin x > a является любое действительное число:  x ∈ ℜ

5. При −1 ≤ a < 1 решение неравенства sin x > a выражается в виде  arcsin a + 2πn < x < π − arcsin a + 2πn,  n ∈ Z 

   Неравенство sin x ≥ a

6. При a > 1 неравенство sin x ≥ a не имеет решений:  x ∈ ∅

7. При a ≤ −1 решением неравенства sin x ≥ a является любое действительное число:  x ∈ ℜ

8. Случай a = 1  x = π/2 + 2πn,  n ∈ Z

9. При −1 < a < 1 решение нестрогого неравенства sin x ≥ a включает граничные углы и имеет вид  arcsin a + 2πn ≤ x ≤ π − arcsin a + 2πn,  n ∈ Z  (рис.1). 

   Неравенство sin x < a

10. При a > 1 решением неравенства sin x < a является любое действительное число:  x ∈ ℜ

11. При a ≤ −1 у неравенства sin x < a решений нет:  x ∈ ∅

12. При −1 < a ≤ 1 решение неравенства sin x < a лежит в интервале  − π − arcsin a + 2πn < x < arcsin a + 2πn,  n ∈ Z   

   Неравенство sin x ≤ a

13. При a ≥ 1 решением неравенства sin x ≤ a является любое действительное число:  x ∈ ℜ

14. При a < −1 неравенства sin x ≤ a решений не имеет:  x ∈ ∅

15. Случай a = −1  x = − π/2 + 2πn,  n ∈ Z

16. При −1 < a < 1 решение нестрогого неравенства sin x ≤ a находится в интервале  − π − arcsin a + 2πn ≤ x ≤ arcsin a + 2πn,  n ∈ Z 

   Неравенство cos x > a

17. При a ≥ 1 неравенство cos x > a не имеет решений:  x ∈ ∅

18. При a < −1 решением неравенства cos x > a является любое действительное число:  x ∈ ℜ

19. При −1 ≤ a < 1 решение неравенства cos x > a имеет вид  − arccos a + 2πn < x < arccos a + 2πn,  n ∈ Z  (рис.3). 

   Неравенство cos x ≥ a

20. При a > 1 неравенство cos x ≥ a не имеет решений:  x ∈ ∅

21. При a ≤ −1 решением неравенства cos x ≥ a является любое действительное число:  x ∈ ℜ

22. Случай a = 1  x = 2πn,  n ∈ Z

23. При −1 < a < 1 решение нестрогого неравенства cos x ≥ a выражается формулой  − arccos a + 2πn ≤ x ≤ arccos a + 2πn,  n ∈ Z  (рис.3). 

   Неравенство cos x < a

24. При a > 1 неравенство cos x < a справедливо при любом действительном значении x:  x ∈ ℜ

25. При a ≤ −1 неравенство cos x < a не имеет решений:  x ∈ ∅

26. При −1 < a ≤ 1 решение неравенства cos x < a записывается в виде  arccos a + 2πn < x < 2π − arccos a + 2πn,  n ∈ Z 

   Неравенство cos x ≤ a

27. При a ≥ 1 решением неравенства cos x ≤ a является любое действительное число:  x ∈ ℜ

28. При a < −1 неравенство cos x ≤ a не имеет решений:  x ∈ ∅

29. Случай a = −1  x = π + 2πn,  n ∈ Z

30. При −1 < a < 1 решение нестрогого неравенства cos x ≤ a записывается как  arccos a + 2πn ≤ x ≤ 2π − arccos a + 2πn,  n ∈ Z  

  Неравенство tan x > a

31. При любом действительном значении a решение строгого неравенства tan x > a имеет вид  arctan a + πn < x < π/2 + πn,  n ∈ Z  

   Неравенство tan x ≥ a

32. Для любого значения a решение неравенства tan x ≥ a выражается в виде  arctan a + πn ≤ x < π/2 + πn,  n ∈ Z  

   Неравенство tan x < a

33. Для любого значения a решение неравенства tan x < a записывается в виде  − π/2 + πn < x < arctan a + πn,  n ∈ Z  

   Неравенство tan x ≤ a

34. При любом a неравенство tan x ≤ a имеет следующее решение:  − π/2 + πn < x ≤ arctan a + πn,  n ∈ Z 

  Неравенство cot x > a

35. При любом a решение неравенства cot x > a имеет вид  πn < x < arccot a + πn,  n ∈ Z  (рис.7). 

   Неравенство cot x ≥ a

36. Нестрогое неравенство cot x ≥a имеет аналогичное решение  πn < x ≤ arccot a + πn,  n ∈ Z  (рис.7). 

   Неравенство cot x < a

37. Для любого значения a решение неравенства cot x < a лежит в открытом интервале  arccot a + πn < x < π + πn,  n ∈ Z  (рис.8). 

   Неравенство cot x ≤ a

38. При любом a решение нестрогого неравенства cot x ≤ a находится в полуоткрытом интервале  arccot a + πn ≤ x < π + πn,  n ∈ Z  (рис.8). 

14)Область определения и область значений функции. В элементарной математике изучаются функции только на множестве действительных чисел R. Это значит, что аргумент функции может принимать только те действительные значения, при которых функция определена, т.e. она также принимает только действительные значения. Множество X всех допустимых действительных значений аргумента  x, при которых функция  y = f ( x ) определена, называется областью определения функции. Множество Y всех действительных значений  y, которые принимает функция,называется областью значений функции. Теперь можно дать более точное определение функции: правило (закон) соответствия между множествами  X  и Y, по которому для каждого элемента из множества X можно найти один и только один элемент из множества Y, называется функцией.