Лекции по ТАУ

Лекция 3 Методы математического описания линейных элементов асу

1. Характеристики воздействий и сигналов в асу

Основные виды сигналов: регулярные (детерминированные), нерегулярные (случайные), непрерывные, дискретные.

Сигнал называется регулярным, если его математическим представлением является заранее заданная функция времени, т.е. он описывается конкретной функцией времени.

При исследовании АСУ и их элементов используют ряд стандартных сигналов, называемых типовыми воздействиями. Эти воздействия описываются простыми математическими функциями и легко воспроизводятся при исследовании АСУ. Использование типовых воздействий позволяет унифицировать анализ различных систем и облегчает сравнение их передаточных свойств.

Наибольшее применение в ТАУ находят следующие типовые воздействия:

• ступенчатое;

• импульсное;

• гармоническое;

• линейное.

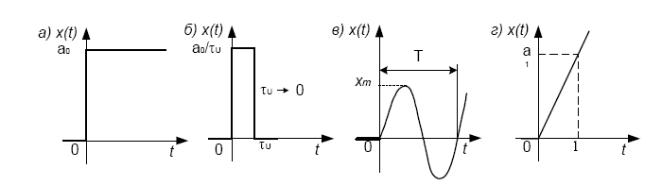
Рис.5. Типовые воздействия в ТАУ

Ступенчатое воздействие:

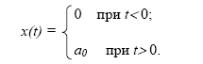
Единичное ступенчатое воздействие:

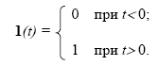
Единичное импульсное воздействие – дельта-функция (Дирака):

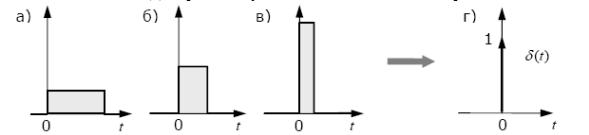
Иногда определяют дельта-функцию как производную от единичного ступенчатого сигнала 1(t):

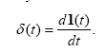
Действительно, эта производная равна нулю при всех значениях t , кроме нуля, где она обращается в бесконечность.

Гармоническое воздействие – сигнал синусоидальной формы, описываемый функцией:

x(t) = xm sinωt , (-∞< t <∞).

Гармонический сигнал, начинающий действовать в момент времени t = 0, описывают при помощи единичной ступенчатой функции:

x(t) = 1(t)∙xm sinωt , (0 ≤t <∞).

Линейное воздействие – воздействие, описываемое функцией:

x(t) = 1(t)∙а₁ t , (0 ≤t <∞).

Коэффициент а₁ характеризует скорость нарастания воздействия x(t).

2. Режимы работы сау

По характеру изменения управляемой величины во времени различают следующие

режимы элемента САУ:

• статический;

• динамический.

Статический режим – состояние элемента САУ, при котором выходная величина не изменяется во времени, т. е. y(t) = const.

Очевидно, что статический режим (или состояние равновесия) может иметь место лишь тогда, когда входные воздействия постоянны во времени. Связь между входными и выходными величинами в статическом режиме описывают алгебраическими уравнениями.

Динамический режим – состояние элемента САУ, при котором входная величина

непрерывно изменяется во времени, т. е. y(t) = var.

Динамический режим имеет место, когда в элементе после приложения входного воздействия происходят процессы установления заданного состояния или заданного изменения выходной величины. Эти процессы описываются в общем случае дифференциальными уравнениями.

Динамические режимы в свою очередь разделяются на:

• переходный;

• установившийся.

Переходный режим – режим, существующий от момента начала изменения входного воздействия до момента, когда выходная величина начинает изменяться по закону этого воздействия.

Установившийся режим – режим, наступающий после того, когда выходная величина начинает изменяться по такому же закону, что и входное воздействие, т. е. наступающий после окончания переходного процесса.