Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Государственный университет имени Шакарима города Семей

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

УМКД Надежность УММ.doc

Скачиваний:

Добавлен:

01.07.2025

Размер:

6 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

Угол заклинивания находится из треугольника

Эта зависимость указывает на то, что с увеличением диаметра ролика и величины l угол заклинивания уменьшается, а с увеличением диаметра отверстия обоймы - увеличивается. Небольшие изменения в размерах l и d приводят к значительному изменению угла заклинивания. Расстояние между осями ролика и звездочки, измеренное в направлении контактной плоскости звездочки, равно:

;

расстояние от центра звездочки до оси прижимной пружины

Момент заклинивания сопровождается приложением нагрузки к элементам механизма. На ролик будут действовать: и - нормальные силы со стороны обойм; и - силы трения на поверхностях соприкосновения ролика с обоймой и звездочкой. Усилием пружины, силами инерции и силой тяжести ролика пренебрегаем. Силы и во время работы механизма смещаются на величины и из-за возникновения площадок смятия.

;

Наметим систему прямоугольных координат началом в центре ролика О, ось абсцисс которой направлена по биссектрисе угла заклинивания. Составим условия самозаклинивания:

;

На основании их совместного решения получим

Пренебрегая величинами и ввиду их малости, получаем

При получим , где - угол на трения поверхности соприкосновения ролика с обоймами. Для муфт обгона угол заклинивания принимают в пределах от 3 до 7.

Вопросы для самоконтроля:

1. Чем является напряжение?

2. Какие различают напряжения?

3. Что такое деформация?

4. Объясните понятие относительная деформация при сдвиге?

5. Назовите единицу измерения напряжения?

6. Запишите формулу для определения напряжения?

7. Что такое упругость?

8. Что вы понимаете под адгезией и аутогезией?

9. Как определяется адгезия?

10. Что такое пластичность и вязкость?

11. На какие системы предложил разделить П.А. Ребиндер?

Рекомендуемая литература

1. Соколов В.М. Основы расчета и конструирования машин и аппаратов пищевых производств. - М.: Колос, 1992-399 с.

2. Соколов В.М. Основы расчета и конструирования деталей и узлов пищевого оборудования. - М.: Машиностроение. 1970-422 с.

3. Харламов С.В. Практикум по курсу “Расчет и конструирование машин и аппаратов пищевых производств”. - Л.: Машиностроение.1971-200 с.

Лекция 18. Кулачковые механизмы.

Содержание лекционного занятия:

1) Область применения. Материалы, применяемые для изготовления кулачков.

2) Основные схемы кулачковых механизмов.

3) Конструкции толкателей.

1) В автоматах пищевой промышленности кулачковые исполнительные механизмы получили широкое распространение среди механических приводов рабочих органов. Этому способствовала возможность обеспечения почти любого закона движения ведомого звена при постоянной угловой скорости вращения вала кулачка. В отдельных случаях скорость вращения кулачка может быть и переменной.

Под кулачковым механизмом понимают совокупность трёх элементов: стойки - базы механизма, ведущего звена - кулачка и ведомого звена - толкателя или коромысла. Кулачок или толкатель, соприкасаясь, образуют высшую кинематическую пару. Кулачку с профилированной поверхностью скольжения, как ведущему звену, чаще всего сообщается вращательное движение, при котором сопряженное с ним звено получает движение в соответствии с заданным законом изменения скорости (ускорения). С целью замены трения скольжения между кулачком и толкателем на трение качения толкатель снабжают роликом. При этом коэффициент полезного действия механизма повышается, а при соответствующем подборе материала и размеров кулачка и ролика их износ снижается.

При соприкосновении роликового толкателя с профилем кулачка центр ролика всегда находится на направлении нормали к профилю в точке их касания и на расстоянии радиуса ролика от профиля кулачка. Геометрическое место точек центра ролика при обратимом движении называется теоретическим профилем или центровым профилем кулачка. При замене теоретического профиля действительным кинематическая сущность механизма не изменяется, т.е. закон движения толкателя остается заданным. Надлежащий контакт высшей кинематической пары обеспечивается силовым (например, с помощью пружины) или геометрическим (конструктивными приемами) замыканием.

Большое количество различных конструктивных форм кулачковых механизмов можно подразделить на:

- Плоские кулачковые механизмы;

- Пространственные кулачковые механизмы;

- Обращенные кулачковые механизмы;

- Кулачковые механизмы с неподвижными кулачками.

2) У плоских кулачковых механизмов траектории движения толкателя и профиля кулачка располагаются в одной плоскости, перпендикулярной к оси вращения кулачка. Ведущее звено плоского механизма может совершать вращательное (рисунок 1, д. е, ж, з) или поступательное (рисунок 1, а, б, в, г) движения. Ведомое звено (толкатель) может совершать поступательное (рисунок 1, а, б, д, е), качательное (рисунок 1, в, ж) движение.

В плоских кулачковых механизмах кулачок выполняется в виде диска с одинарной наружной торцовой рабочей поверхностью сложного профиля или с двойной – в виде паза, выфрезерованного на одной из боковых сторон диска, а также в виде двух кулачков.

В первом случае применено обычное силовое замыкание пары ролик – кулачок (пружины сжатия и растяжения). При применении пазового кулачка замыкание обеспечивается кинематически. При двух кулачках замыкание пары осуществляется вильчатым толкателем с двумя роликами.

Рисунок 1. Схемы плоских кулачковых механизмов

3) В пространственных кулачковых механизмах кулачок выполняется в виде цилиндра с одинарной наружной торцовой (сбоку) рабочей поверхностью сложного профиля – переменной длины по образующим цилиндра (рис.3, а, б) и в виде паза, выфрезерованного на наружной поверхности цилиндра (рис. 3, в, г). В случае применения качающихся толкателей замыкание пары осуществляется так же, как в плоских кулачковых механизмах.

Если продолжение траектории возвратно-поступательного движения ведомого звена (толкателя) проходит через ось вращения кулачка (в пространственных кулачковых механизмах - параллельно сои кулачка), то такой механизм называется центральным, в противном случае – внецентренным (на рисунке 3, в этот вариант показан штрихами; е - эксцентриситет).

Рабочий орган исполнительного механизма может быть связан с ведомым звеном непосредственно или через систему промежуточных звеньев. В последнем случае кулачковый механизм является составной частью более сложного исполнительного механизма; закон движения рабочего органа будет определятся не только профилем кулачка, но и системой промежуточных звеньев.

В обращенных кулачковых механизмах ведущим звеном является толкатель (а), ведомым – кулак (б) (рисунок 4).

В кулачковых механизмах с неподвижным кулачком (рисунок 5) звено 1 вращается относительно точки А. Ролик 3 звена 2 обкатывается по профилю неподвижного кулачка 4, совершая качательное (рисунок 5, а) или поступательное (рисунок 5, б) движение относительно звена 1.

Рисунок 6. Механизмы с неподвижными кулачками

а – для получения движения по заданной траектории;

б – с качающейся кулисой

Рабочий орган кулачкового исполнительного механизма может быть связан с толкателем через промежуточные звенья, количество и конструкция которых зависят от компоновки узла автомата.

Вопросы для самоконтроля:

1. Чем является напряжение?

2. Какие различают напряжения?

3. Что такое деформация?

4. Объясните понятие относительная деформация при сдвиге?

5. Назовите единицу измерения напряжения?

6. Запишите формулу для определения напряжения?

7. Что такое упругость?

8. Что вы понимаете под адгезией и аутогезией?

9. Как определяется адгезия?

10. Что такое пластичность и вязкость?

11. На какие системы предложил разделить П.А. Ребиндер?

Рекомендуемая литература

1. Соколов В.М. Основы расчета и конструирования машин и аппаратов пищевых производств. - М.: Колос, 1992-399 с.

Лекция 19. Расчет и конструирование кулачковых механизмов.

Содержание лекционного занятия:

1. Выбор способа замыкания цепи кулачкового механизма.

2. Определение характеристики пружин при силовом замыкании кулачка.

3. Расчет центральных кулачковых механизмов с возвратно-поступательным движением толкателя.

1. Способ замыкания кулачкового механизма в значительной степени определяет размеры его звеньев и силовые нагрузки.

Для осуществления кинематического замыкания применяют пазовые кулачки, рамочные толкатели или толкатели с двумя роликами, сдвоенные кулачки, действующие на один толкатель, и сдвоенные кулачки, действующие на два кинематически связанных толкателя. Силовое замыкание обычно выполняется посредством пружины, обеспечивающей контакт толкателя с кулачком через ролик.

Основное преимущество силового замыкания по сравнению с кинематическим - невозможность заклинивания механизма в период возвращения толкателя. Поэтому углы давления в этот период могут быть близкими к 90°; это позволяет при заданной продолжительности периодов движения уменьшить габариты кулачка или при заданных габаритах уменьшить продолжительность периода движения.

Для приближенного определения минимального радиуса теоретического профиля кулачка по допустимому углу давления при длине отрезков и , соответствующих периодам удаления и возвращения (соответственно углам и ):

;

При одновременном учете углов давления в период удаления и возвращения толкателя (например, при пазовом кулачке) ось вращения кулачка должна проходить через точку А. Если же кинематическое замыкание заменить силовым, то при той же длине отрезка ось вращения кулачка может быть перенесена в точку А-г и радиус минимальной окружности кулачка уменьшится до размера (вместо ). При сохранении минимального радиуса ось вращения кулачка может быть перенесена в точку , отрезок увеличивается до размера и период удаления сократится до

2) Основная роль пружины при силовом замыкании сводится к обеспечению контакта ролика толкателя и рабочего профиля кулачка в течение всего периода возвращения. Если пружина подобрана неправильно, то возможен разрыв кинематической цепи и, следовательно, нарушение нормальной работы механизма.

В период работы кулачковой пары пружина в зависимости от конструкции узла может работать на сжатие или на растяжение.

В обоих случаях зависимость силы Рп цилиндрической пружины от ее деформации бывает линейной и описывается уравнением

где - предварительное натяжение пружины, предварительной деформацией ; - жесткость пружины; l - деформация пружины.

Чтобы подобрать пружину, отвечающую требованиям нормальной работы кулачкового механизма с силовым замыканием, необходимо построить график суммарной силы, действующей на толкатель, т. е. силы , где перемещение толкателя, и совместить его с графической характеристикой пружины. Существуют несколько методов построения графической зависимости , выбор одного из которых определяется условиями работы механизма.

Рассмотрим методы определения характеристик пружины. Толкатель (звено 2) находится под действием следующих сил:

- реакция звена 3, найденная при кинетостатическом расчете группы 3 - 4 с учетом технологической силы и сил инерции;

— реакция толкателя, проходящая через центр качания;

— реакция пружины, работающей на растяжение;

— реакция кулачка, направленная по нормали к профилю. Из условий динамического равновесия толкателя

В правой части этого уравнения силы считаются положительными, если их момент соответствует направлению удаления толкателя. Для силы положительным принято считать обратное направление.

Минимальное значение силы , при котором еще обеспечивается замыкание кинематической цепи ( ), равно

Отношение характеризует запас пружины, гарантирующий от размыкания кинематической цепи.

Определяя последовательно значения силы для достаточно большого числа положений механизма в период удаления и возвращения и измеряя одновременно для каждого положения длину l = OD, построим график . На этом графике кривая 1 соответствует периоду удаления, а кривая 2 - периоду возвращения. Так как не может быть меньше нуля, то сила должна быть больше на величину

Для определения характеристики пружины совмещаем графики и . Зависимость представлена наклонной прямой 3 с угловым коэффициентом, равным , где и - соответственно масштабы по осям ординат и абсцисс.

Если прямая пересечет линию 2 (показана пунктиром), то в точке пересечения А произойдет разрыв кинематической цепи, так как пружина не может создать ускорения, соответствующего профилю кулачка.

Отрезки ординат, заключенные между прямой 3 и кривой 1 или 2, представляют собой запас пружины. Построив графики 1 и 2, задаются коэффициентом запаса 6 и строят кривую . Если кривые 1 и 2 пересекаются, как это показано на рисунке 10, то график достаточно строить по большим положительным значениям Характеристика пружины, обеспечивающая заданный коэффициент запаса, должна касаться кривой . Из бесчисленного множества характеристик должна быть выбрана такая, при которой разность меньше, так как эта величина характеризует наибольшее давление кулачка на ролик:

Кроме того, при выборе характеристики пружины должны быть учтены конструктивные возможности. При чрезмерно «мягких» характеристиках обычно возникают меньшие давления кулачка на ролик, но требуется большая длина пружины, так как .

Пружины обычно подбирают по справочникам, в которых заданы для каждой винтовой пружины - допустимая сила и жесткость одного или десяти витков. В этом случае по ориентировочному значению выбирают диаметр пружины D и диаметр проволоки d, при которых . Затем определяют число рабочих витков

где определяется по и ориентировочным значениям и . Длина рабочей части свободной пружины , где - зазор между витками.

Этот метод определения характеристики пружин, основанный на силовом расчете всего механизма во многих положениях, позволяет одновременно определить реакции в кинематических парах.

3) При конструировании центральных кулачковых механизмов с возвратно – поступательным движением толкателя к числу заданных параметров относятся: -полное перемещение толкателя в одном направлении; , , , - углы поворота кулачка соответственно при удалении толкателя от центра вращения кулачка, дальнем стоянии, возвращении и ближнем стоянии; - угловая скорость вращения кулачкового вала; и - допустимые углы давления на участках удаления и возвращения толкателя; - сила полезного технологического сопротивления (статическая), приведенная к направлению перемещения толкателя; - масса толкателя и связанных с ним деталей, приведенных к толкателю; ЗДРО – закон движения рабочего органа (толкателя).

К числу расчетных параметров относятся: , , , - интервалы соответственного удаления, дальнего стояния, возвращения, ближнего стояния толкателя; и - радиусы начальных окружностей теоретического и действительного профилей кулачка; параметры ролика, оси ролика, текущие радиус – векторы профиля кулачка и другие данные, относящиеся как к отдельным элементам кулачкового механизма, так и к механизму в целом.

С целью уточнения и рационализации расчетов кулачковых механизмов рекомендуется пользоваться табличными значениями безразмерных позиционных коэффициентов (БПК) времени и экстремальными значениями (пиками) , , .

При конструировании кулачковых механизмов необходимо стремиться к получению механизма с наименьшими габаритными размерами при обеспечении прочности кулачка и ролика и точности передачи закона движения.

Значительную роль в обеспечении незаклинивания и прочности кулачкового механизма играет угол давления (угол между направлением движения толкателя и нормалью к профилю кулачка в точке касания его толкателем. Для центрального кулачкового механизма с возвратно – поступательным движением угол давления выражается зависимостью

где - угол поворота кулачка, равный или .

В случае применения для толкателя симметричных ЗДРО допускают с достаточной для практики точностью, что скорость движения толкателя и угол давления становятся максимальными на середине пути толкателя, т.е. при 0,5. Тогда, принимая допустимый угол давления (из практического опыта, расчёта или рекомендаций), равный максимальному, находим

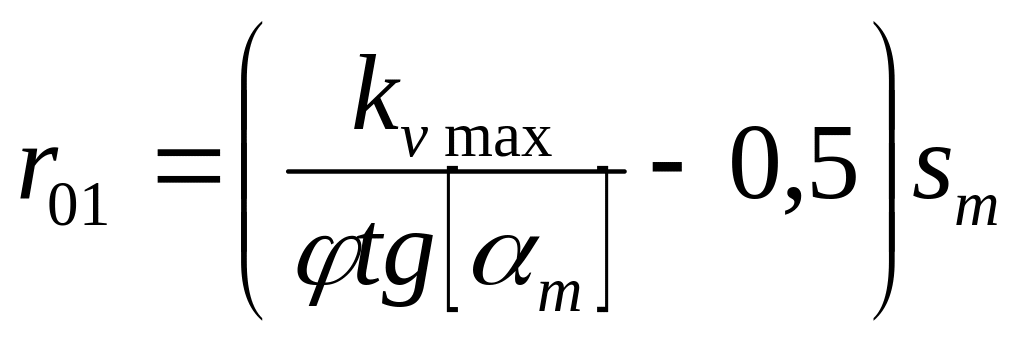где - максимально допустимый угол давления, равный или .

Радиус начальной окружности кулачка влияет на условия прочности и износостойкости элементов кулачкового механизма.

Вопросы для самоконтроля:

1. Чем является напряжение?

2. Какие различают напряжения?

3. Что такое деформация?

4. Объясните понятие относительная деформация при сдвиге?

5. Назовите единицу измерения напряжения?

6. Запишите формулу для определения напряжения?

7. Что такое упругость?

8. Что вы понимаете под адгезией и аутогезией?

9. Как определяется адгезия?

10. Что такое пластичность и вязкость?

11. На какие системы предложил разделить П.А. Ребиндер?

Рекомендуемая литература

1. Соколов В.М. Основы расчета и конструирования машин и аппаратов пищевых производств. - М.: Колос, 1992-399 с.

Лекция 20. Звездчатые механизмы.

Содержание лекционного занятия:

1. Область применения. Конструктивные схемы.

2. Проектирование нормальных профилей зубьев звездочки.

3. Расчет звездчатых механизмов.

1) Звездчатые механизмы относятся к механизмам с периодическим движением ведомого звена при постоянном передаточном числе в большей части движения.

Ведущее звено 1 вращается с постоянной угловой скоростью , сообщая движение ведомому звену 2 лишь в период зацепления цевок с зубьями ведомого звена-звездочки (рисунок 1). После выхода из зацепления последней цевки движение ведомого звена прекращается. При этом положение его фиксируется цилиндрической поверхностью ведущего звена, скользящей по вогнутой поверхности башмака ведомого звена.

Механизм обеспечивает равные периоды движения и покоя, причем в данном случае за один оборот ведущего звена ведомое звено поворачивается за один оборот на 90º. Каждый период движения ведомого звена начинается при вхождении первой цевки в первый паз звездочки, который профилируется так, чтобы обеспечить постепенное увеличение угловой скорости звездочки от до . При зацеплении второй, третьей и четвертой цевок с соответствующими профилями зубьев звездочки передаточное число остаётся постоянным. При выходе же пятой цевки из последнего паза звёздочки угловая скорость последней уменьшается до нуля, после чего следует период остановки. Постоянство передаточного числа в основной период движения обеспечивается профилированием зубьев звездочки по кривым, эквидистантным эпициклоиде.

Рисунок 1. Схема звездчатого механизма.

Основные достоинства звёздчатой передачи:

- Возможность равномерного движения звена на значительной части угла поворота;

- Возможность изменения коэффициента К в широких пределах при различных углах поворота ведомого звена.

В некоторых случаях применяются звёздчатые механизмы с двумя и более периодами движения за один оборот цевочного колеса; продолжительность этих периодов движения может быть различной.

Основные недостатки звёздчатых механизмов:

- Интенсивное изнашивание цевок;

- Необходимость высокой точности изготовления и монтажа для обеспечения условий нормальной работы.

Во избежание интенсивного изнашивания цевок, помимо использования износостойких материалов, рекомендуется применять так называемое внецентроидное цевочное зацепление, в котором цевки вынесены за пределы начальной окружности цевочного колеса.

2) Рассмотрим проектирование нормальных профилей зубьев звездочки. Если начальную окружность а цевочного колеса перекатывать без скольжения по начальной окружности б звездочки (рисунок 2), то любая точка (например, точка А окружности а на плоскости, жестко связанной с окружностью б, опишет эпициклоиду, построить которую можно следующим образом.

Выберем на относительной траектории центра О₁ ряд положений этой точки 1", 2", З", 4", 5", 6" и т. д.; из этих точек, как из центров, проведем окружности с радиусом r₁, на которых будут расположены последовательные положения точки А. Отметим на окружности б точки 1, 2, 3 и т. д. касания с окружностью а. Так как начальные окружности перекатываются без скольжения, то точки касания 1 , 2', 3' и т. д. на окружности а соответствуют равным дугам на окружности б, т. е. 0 - 1 = 0 -1; 1 -2' = 1-2; 2'-3' = 2-3 и т.д.

Рисунок 2. Построение теоретического профиля зуба звездочки

Положение точки А₃ на эпициклоиде определится пересечением окружности радиуса r₁ из точки 3" с дугой радиуса 0—3' из точки 3, причем точки 3' и Аз будут расположены на одинаковом расстоянии от центра 0₂. Аналогично находят остальные точки этой и симметричной с ней ветви эпициклоиды. Профиль зуба звездочки образуют как огибающую окружностей радиуса цевки, проведенных из точек эпициклоиды.

Так как точка касания начальных окружностей а и б есть мгновенный центр скоростей в относительном движении этих окружностей, то она является и полюсом зацепления. Центр кривизны эпициклоиды всегда расположен на окружности б.

Пазы для первой и последней цевок могут быть выполнены различного профиля в зависимости от требований к плавности зацепления. Если профиль зуба, с которым встречается первая цевка, выполнить по такой же кривой, как и следующие зубья, то постоянство передаточного числа обеспечивается во все время движения звездочки; однако при этом в начальное мгновение происходит «жесткий» удар.

Вопросы для самоконтроля:

1. Чем является напряжение?

2. Какие различают напряжения?

3. Что такое деформация?

4. Объясните понятие относительная деформация при сдвиге?

5. Назовите единицу измерения напряжения?

6. Запишите формулу для определения напряжения?

7. Что такое упругость?

8. Что вы понимаете под адгезией и аутогезией?

9. Как определяется адгезия?

10. Что такое пластичность и вязкость?

11. На какие системы предложил разделить П.А. Ребиндер?

Рекомендуемая литература

1. Соколов В.М. Основы расчета и конструирования машин и аппаратов пищевых производств. - М.: Колос, 1992-399 с.

Лекция 21. Расчет и конструирование звездчатых механизмов.

Содержание лекционного занятия:

1. Расчет звездчатых механизмов.

2. Определение основных параметров звездчатого механизма.

1) На рисунке 1 пунктиром показаны графики угловых перемещений и угловых перемещений звёздочки в функции углов поворотов цевочного колеса при наличии «жёсткого удара». Передаточное число в этом случае определяется из соотношения

На тех же графиках сплошными линиями изображены и при отсутствии «жёстких ударов», причём, на участках в начале и в конце движения звёздочки скорость принята изменяющейся по линейному закону. В этом случае на участке равномерного движения передаточное число меньше передаточного числа :

Рисунок 3. Законы движения звёздочки:

а – график угла поворота; б – график угловой скорости

Соответственно передаточному числу на участке равномерного движения должны быть подобраны радиусы и начальных окружностей:

2) Если паз, в который входит первая цевка, очерчен эпициклоидой (теоретический профиль) (рисунок 4), то для безударного начала зацепления центр А₀ первой цевки в это мгновение должен располагаться в точке касания окружности а радиуса r₁, проведенный из центра 0₁ и эпициклоиды э первого ряда звездочки. Угол между линией центров и радиусом , проведенным через основание эпициклоиды, есть угол поворота звездочки в период разгона и соответствует углу поворота цевочного колеса. Закон движения звездочки в период разгона можно получить следующим образом.

Рисунок 4. Профилирование первого зуба звездочки и определение закона движения в период разгона (а); звездчатая передача с двумя периодами движения (б): 1 – цевочное колесо с двумя группами цевок; 2 - звездочка

Разделим дугу на несколько равных частей (например, на четыре части) точками и проведем через эти точки окружностей с центром в точке до пересечения с эпициклоидой э. Из точек пересечения и на окружности С сделаем засечки радиусом r₁. Полученные точки и показывают положение центра цевочного колеса в обращении движении при его повороте на углы 1/4 , 1/2 , 3/4 и . Дуги , , , соответствуют искомым углам поворота звездочки в период разгона.