2. Задание для выполнения курсовой работы (содержание

пояснительной записки)

1. Составление математического описания системы

1.1. Вычертить схему (рис. 1) и привести исходные данные выполняемого варианта работы.

1.2. Записать уравнения во временной области, привести их операторные преобразования и найти передаточные функции для всех элементов системы.

1.3. Составить полную и линеаризованную структурные схемы.

1.4. Определить численные значения коэффициентов связи и постоянных времени неизменяемой части системы.

2. Анализ установившегося режима

2.1. Составить структурную схему для установившегося режима.

2.2. Определить необходимый коэффициент передачи замкнутого контура системы k_Р обеспечивающий в замкнутой системе статическую ошибку регулирования n_З не более 5 % от регулируемой частоты вращения, если задан диапазон регулирования D=10:1 при максимальной частоте вращения, равной номинальной n_Н.

Определить требуемый коэффициент усиления k_I операционного усилителя У1.

2.3. Определить значение переменных (U_d,U₃,U₂,U₁,U_ТГ,U_ЗАД) для режима работы с заданной частотой вращения n_ЗАД.

2.4. Определить статические отклонения n частоты вращения вала привода от заданного значения n_ЗАД в установившемся режиме в системе без обратной связи (n_Р) и в замкнутой системе (n_З) при ступенчатом воздействии основных возмущений М_С=М_Н и U_C=0,1· U_{d ЗАД} . Дать сравнительную оценку точности поддержания частоты вращения в статике для разомкнутой и замкнутой системы.

3. Исследование динамики системы

3.1. Построить аппроксимированную логарифмическую амплитудно-частотную характеристику (ЛАЧХ) системы в разомкнутом состоянии. Проверить устойчивость замкнутой системы.

3.2. Построить желаемую ЛАЧХ системы в разомкнутом состоянии, исходя из следующих требований: перерегулирование скорости  по управляющему воздействию не более 20…30 %; время переходного процесса – минимальное; и ослабление всех возмущений – максимальное во всем диапазоне регулирования.

3.3. Найти ЛАЧХ последовательного корректирующего устройства, определить передаточную функцию корректирующего устройства, выбрать схему и определить параметры Z1 и Z2 корректирующего устройства.

3.4. Рассчитать кривую переходного процесса, отклонение n_З частоты вращения вала привода от заданного значения n_ЗАД при приложении заданного возмущения. Расчет производить моделированием САУ на ЭВМ. По полученной кривой оценить качество переходного процесса.

3. Методические указания по выполнению курсовой работы

К первой части

Математическое описание системы приводится на основе составления системы дифференциальных уравнений для элементов системы при общепринятых допущениях.

• Электродвигатель постоянного тока независимого возбуждения с рабочей машиной при допущениях постоянного магнитного потока двигателя с компенсированной реакцией якоря двигателя, с абсолютно жесткими механическими соединениями и постоянном моменте инерции J привода описывается системой уравнений. Система состоит из дифференциальных уравнений баланса напряжений якорной цепи и движения привода, а так же соотношений между ЭДС Е и частотой вращения n, электромагнитным моментом М и током I якорной цепи

(1.1)

где C_Е – коэффициент, учитывающий магнитный поток и конструктивное исполнение электродвигателя.

• Тиристорный преобразователь ТП с СИФУ описывается неоднородным дифференциальным уравнением первого порядка

, (1.2)

где Т_П – постоянная времени (Т_П=0,05 с для всех вариантов);

k_П – коэффициент определяемый статической характеристикой ТП.

• Операционные усилители У1, У2 описываются передаточной функцией

, (1.3)

где Z_ОС(р) и Z_ВХ(р) – операторные сопротивления цепей обратной связи и входного данного операционного усилителя.

При этом операторное сопротивление активной цепи равно R, емкостной – 1/С_Р , индуктивной – L_Р. При сложных соединениях этих сопротивлений применяют правила, аналогичные правилам расчета соединений действительных сопротивлений. Если на вход операционного усилителя (У2 в задании) прикладывается несколько различных воздействий U₁, U₂ и т. д. с входными сопротивлениями Z1, Z2 и т. д., то операционный усилитель описывается соотношениями

(1.4)

где U₁, U₂ … берутся со знаком, соответствующим полярности напряжения на входе операционного усилителя, т. е. при Z_ОС=Z1=Z2=… операционный усилитель может служить сумматором в алгебраическом смысле слова.

• Тахогенератор представляется в виде линейного безинерционного усилительного звена с передаточным коэффициентом k_ТГ.

• Фильтр на выходе тахогенератора можно рассматривать как отдельное звено с входным напряжением U_ТГ и выходным U₁. Такое допущение основывается на том, что внутреннее сопротивление тахогенератора можно считать пренебрежимо малым, а нагрузочное сопротивление R2 на порядок больше внутреннего сопротивления фильтра. Полярность U_ТГ подбирается такой, чтобы в установившемся режиме сигнал обратной связи на входе У2 был обратным по знаку сигналу U_ЗАД. Постоянная времени фильтра Т_Ф определяется произведением С_фR_Ф.

Рекомендуется после математического описания элемента системы во временной области приводить его изображение по Лапласу при нулевых начальных условиях, передаточную функцию и структурную схему – полную с графическим изображением статической характеристики, если таковая имеется, и линеаризованную – с указанием конкретной передаточной функции элемента.

При определении передаточной функции электродвигателя за выходную переменную следует принимать частоту вращения вала n, за входное задающее воздействие – напряжение U_d , в качестве возмущающих воздействий – момент статического сопротивления М_С и отклонения напряжения сети  U_С. Следует учесть, что динамические свойства электродвигателя характеризуются двумя постоянными времени: электромагнитной Т_Я=L_ЯЦ/R_ЯЦ и электромеханической Т_М=J·R_ЯЦ/С_Е². Коэффициент передачи двигателя относительно U_d определяется соотношением k_d=1/C_E. Сравнивая передаточные функции электродвигателя по задающему воздействию и колебательного звена, можно определить коэффициент затухания . При 0<<1 двигатель представляется колебательным звеном, при >1 – апериодическим звеном второго порядка. Собственная частота _d колебаний электродвигателя равна .

В целом рассматриваемая система электропривода представляет собой одноконтурную замкнутую САУ с последовательным корректирующим устройством.

Прямой канал полной структурной схемы САУ включает в себя последовательное соединение звеньев: сумматора У2 с входными воздействиями: задающим U_ЗАД, обратной связью U₁ и выходным воздействием U₂; коррекции У1 со входом U₂ и выходом U₃ ; тиристорного преобразователя, состоящего из инерционного звена 1-го порядка с коэффициентом усиления, равным 1, и безинерционного линейного звена с таблично заданной нелинейной статической характеристикой преобразователя (входным воздействием преобразователя служит U₃ , а выходным – U_d); электродвигателя с указанными выше воздействиями U_d, n,  U_С, М_с.

Канал обратной связи состоит из усилительного звена тахогенератора ТГ с коэффициентом передачи k_тг, входным воздействием n, выходным U_тг и из фильтра в виде инерционного звена 1-го порядка.

Линеаризованная структурная схема САУ получается, если полные переменные X(U_3АД , U₂ , U₃ , U_d ,  U_С, I, М, М_с, n, U_тг, U₁ ) представить в виде суммы Х_А+Х, где Х_А – значение переменных в рабочей точке статических характеристик звеньев. После сокращения статических составляющих левой и правой части уравнений звеньев линеаризованные структурные схемы звеньев отразят зависимость между приращениями входных и выходных переменных ( U_зад,  U₂, …,  U₁ ). Форма записи передаточных функции линейных звеньев при этом не изменяется, а статические характеристики нелинейных безинерционных звеньев будут представлены в виде коэффициентов динамической линеаризации в рабочей точке.

При расчёте численных значений коэффициентов передачи и постоянных времени звеньев САУ следует приводить формулу в буквенных обозначениях параметров, затем то же выражение с подставленными в него значениями параметров САУ и после этого конечный результат с указанием размерности в системе СИ. Конструктивный коэффициент С_Е электродвигателя может быть рассчитан по уравнению баланса напряжений якоря двигателя в установившемся номинальном режиме, т. е.

, (1.5)

где переменные U_н, I_н, n_н определены данными электродвигателя (табл. 2), а сопротивление R_ЯД собственно цепи якоря двигателя составляет 0,5 R_ЯЦ сопротивления всей якорной цепи (табл. 2).

Из графической зависимости U_d (U_з) (табл. 1), построенной в одинаковом масштабе переменных обеих осей, определяется коэффициент k_п динамической линеаризации статической характеристики тиристорного преобразователя. , или графически k_п равен тангенсу угла наклона касательной, проведённой к статической характеристике рабочей точки А. Рабочая точка А определяется значением выпрямленного напряжения U_d|_A в режиме идеального холостого хода электродвигателя. Необходимо определить значение k_п в трёх рабочих точках:

k_{п мин} – при максимальном значении U_d в заданном диапазоне регулирования D, т. е. U_{d мин}=U_н/D, k_{п мин} используется при определении коэффициента k₁ корректирующего звена (п. 2.2);

k _{п макс} – в точке с максимальным наклоном статической характеристики в пределах диапазона регулирования, k_{п макс} используется для определения динамического сомножителя передаточной функции корректирующего звена (пп. 3.1…3.3);

k_{п зад} – при заданном значении выпрямленного напряжения, т. е. при

U_{d зад}=С_Е·n_зад, k_{п зад} используется для построения ЛАЧХ САУ в заданном рабочем режиме.

Ко второй части задания

Структурная схема для установившегося режима составляется на основе уравнений элементов САУ в статике или на основе линеаризованной структурной схемы САУ формальным путём приравнивания оператора p к 0. Следует обратить внимание, что последним способом установившийся режим работы двигателя может быть описан лишь на основе полной передаточной функции двигателя по отношению к U_d и М_с с выходом по частоте вращения, т. е. с учётом внутренней обратной связи двигателя.

По полученной структурной схеме в установившемся режиме можно определить статическое отклонение частоты вращения n вала при приложении М_с=М_н в разомкнутой системе без обратной связи (без ТГ и фильтра) – n_рМс и в замкнутой САУ n_зМс. Нетрудно убедиться, что соблюдается равенство

, (2.1)

k_р=k₁ · k_п·k_d·k_тг , (2.2)

где k_р – коэффициент передачи замкнутого контура САУ в разомкнутом состоянии.

Отклонение n_рМс рассчитывается непосредственно из структурной схемы в установившемся режиме, при этом, согласно (1.1), М_с=М_н=С_Е·I_н.

Учитывая, что относительное падение частоты вращения в статике при приложении М_с имеет максимальную величину при минимальной частоте вращения в пределах заданного диапазона регулирования D и, исходя из требований п. 2 задания, имеем соотношение

n_зМс0,05 n_н / D. (2.3)

Тогда необходимый коэффициент передачи k_{р мин} может быть найден из уравнения (2.1), а требуемый из условий статики коэффициент k_I операционного усилителя У1 из уравнения (2.2) (учитывая, что k_{р мин} в качестве сомножителя имеет коэффициент передачи тиристорного преобразователя, равный k_{п мин}, найденный в первой части курсовой работы).

Рекомендуется после определения k_I найти, согласно (п. 2.2), коэффициенты k­_{р макс} и k_{р зад}, при этом в соотношении (2.2) меняется лишь значение коэффициента передачи тиристорного преобразователя (k _{п макс} и

k_{п зад}). Значения k_{р зад} используется при выполнении пп. 2.4; k_{р макс} – при выполнении пп.3.1…3.3 задания.

К третьей части задания

Как известно из теории автоматического управления, устойчивость замкнутой САУ может быть определена с помощью критерия Найквиста, который в случае рассматриваемой устойчивой САУ в разомкнутом состоянии и анализе её частотных характеристик в логарифмическом масштабе сводится к условию, чтобы

|_р(_с)|<180 , (3.1)

где частота среза _с системы определяется значением частоты точки пересечения ЛАЧХ САУ в разомкнутом состоянии и оси абцисс (L_р(_с)=0).

Показатели качества переходного процесса в замкнутой САУ зависят от запаса устойчивости по фазе (=180–|_р(_с)|) и по амплитуде L(L равно абсолютному значению L_р при частоте, где |_р|=180). В частности это иллюстрируется на рис. 2, где представлены зависимости перерегулирования  в замкнутой САУ по задающему воздействию  и L.

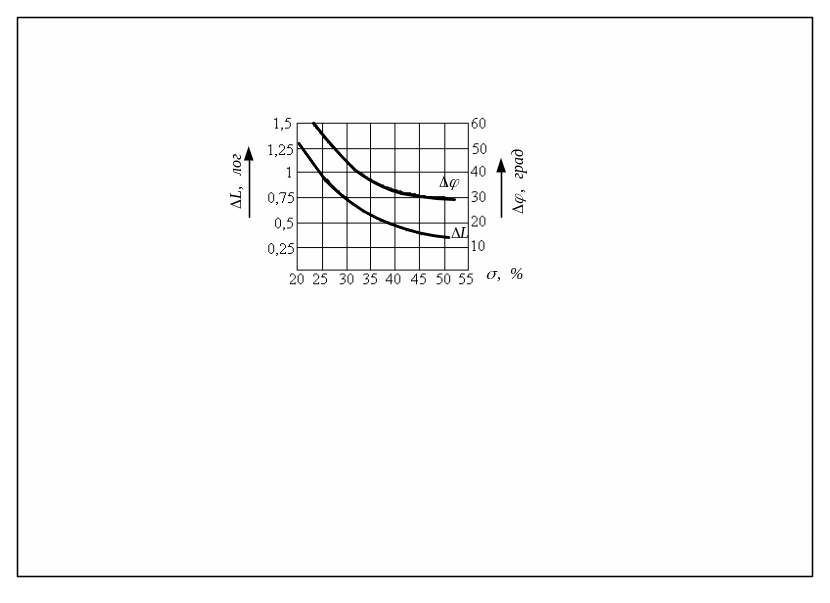
Рис. 2. Кривые запаса устойчивости по модулю L и по фазе 

от перерегулирования 

В работе рассматривается минимально – фазовая система, т. е. система, состоящая в разомкнутом состоянии из звеньев, имеющих однозначную зависимость между АЧХ и ФЧХ. Для такой системы анализ устойчивости можно провести по аппроксимированной ЛАЧХ системы в разомкнутом состоянии без построения ФЧХ. Значение _i при любой выбранной частоте _i для минимально-фазовой системы может быть приближённо определено по усреднённому наклону ЛАЧХ в этой частоте и равно

_i_ср_i·90, (3.2)

. (3.3)

Усреднённый наклон _ср_i определяется путём нахождения координаты L_В_i, отстоящей на одну декаду в сторону высоких частот, т. е. L_В_i=L10_i, и координаты L_Н_i, отстоящей на одну декаду в сторону низких частот, т. е. L_Н_i=L0,1_i.

Некорректированная САУ в разомкнутом состоянии состоит из последовательно соединённых звеньев:

– усилительного – усилителя У1 с коэффициентом передачи k_I, найденным из условия статики во второй части задания;

– инерционного – тиристорного преобразователя с коэффициентом передачи k_п и частотой сопряжения _п=1/Т_п;

– колебательного – электродвигателя с коэффициентом передачи k_d и собственной частотой колебаний ;

– усилительного – тахогенератора с коэффициентом передачи k_тг;

– инерционного – фильтра с единичным коэффициентом передачи и частотой сопряжения _ф=1/Т_ф.

При проверки устойчивости некорректированной САУ и построении желаемой ЛАЧХ системы в разомкнутом состоянии (пп. 3.1 и 3.2) коэффициенты передачи всех звеньев (в том числе и желаемой k_I) могут быть объединены в соответствии с п. 2.2. в один коэффициент k_р. Следует учитывать, что наихудшие условия, с точки зрения устойчивости, при заданных параметрах динамических звеньев будут находиться при максимальном значении k_р в требуемом диапазоне регулирования, т. е. при k _{р макс}=k_р (см. указания ко второй части).

Процесс построения аппроксимированной ЛАЧХ некорректированной САУ в разомкнутом состоянии можно ускорить, если воспользоваться следующей методикой:

• определить значение ординаты L_p(0), равное lgk_{р макс}, и абсцисс частот сопряжения и колебаний lg_п, lg_d, lg_ф;

• на низких частотах графика L_p^нк_­­() отложить ординату, равную L_p(0), и провести через эту ординату прямую с нулевым наклоном (параллельно оси абсцисс) до ближайшей меньшей собственной частоты одного из звеньев;

• по мере увеличения частоты изменять наклон ЛАЧХ на –1 лог/дек в абсциссах, соответствующих частотам, сопряжения инерционных звеньев, и на –2 лог/дек в абсциссах, соответствующих собственной частоте колебательного звена.

На рис. 3 приведена наиболее типичная для заданных вариантов ЛАЧХ L_p^нк_­­() некорректированной САУ в разомкнутом состоянии, построенная по данной методике. Параметры вариантов системы таковы, что некорректированная САУ либо неустойчива, либо имеет малый запас устойчивости, не удовлетворяющий требованиям обеспечения заданного качества регулирования. Для примера (рис. 3) значение ФЧХ в частоте _с^нк среза некорректированной САУ в соответствии с (3.2) и (3.3) составит L_в­­(_с^нк)=–4лог; L_н(_с^нк)=1,57 лог и _p^нк_­­(_с^нк) = [L_в­­(_с^нк)–L_н(_с^нк)] · 45= =(–4–1,57) · 45=–250,6 т. е. некорректированная САУ неустойчива, т. к. |_p^нк_­­(_с^нк)|>180.

Рис. 3. К построению ЛАЧХ: некорректированной САУ L_Р^НК,

желаемой L_Р^ЖЕЛ и коррекции L_К^'

При построении желаемой ЛАЧХ системы в разомкнутом состоянии в соответствии с требованием обеспечения перерегулирования  по задающему воздействию не более 30 % необходим запас по фазе 45 и по амплитуде L0,75 лог (рис. 2). Это соответствует фазе _p^жел(_с)135 или, согласно (3.2) и (3.3), соотношению

|L_в­­(_с) – L_н(_с)|3 лог. (3.4)

Следует учитывать, что требование минимального времени регулирования выполняется при максимально возможной величине частоты _с скорректированной САУ, а требование максимального ослабления возмущений выполняется при минимальном уменьшении координат L_p в области низких частот (до _с).

Частоты сопряжения на участках желаемых ЛАЧХ L_p^ЖЕЛ() с различными наклонами следует выбирать с таким расчётом, чтобы передаточная функция корректирующего устройства была реализована наиболее просто, что достигается, если частоты сопряжения участков желаемой ЛАЧХ выбраны равными частотам сопряжения звеньев исходной некорректированной системы.

В примере рис. 3, если стремиться в области существенных частот (области частот _с) к желаемой ЛАЧХ, близкой к оптимуму с однократным интегрированием, удобно принять частоты сопряжения участков с наклоном –1 лог/дек и –2 лог/дек, равной _d, участков с наклоном –2 лог/дек и –3 лог/дек, равной _ф, и частоту сопряжения ₄ участков с наклонами –3 лог/дек и –4 лог/дек достаточно высокой, чтобы она не влияла на запас устойчивости  и L, т. е. ₄>10₀. Для такой конфигурации L_Р^ЖЕЛ() (см. рис. 3) L определяется координатами L_Р^ЖЕЛ при абсциссе, лежащей на середине отрезка между lg_d и lg_ф, т. е. должно соблюдаться условие

(или lg_С lg_Ф–0,75). (3.5)

Аналогично определяется L_H(_С)=1 лог (поскольку наклон L_Р^ЖЕЛ() до частоты _С равен –1 лог/дек, а lg k_{Р МАКС}>1):

L_В(_С)= – (lg _d – lg _С) – 2(lg _Ф – lg _d) – 3(lg _C – lg _Ф+1).

Тогда согласно (3.4),

|L_в­­(_с)– L_н(_с)|=|lg _d –2 lg _С +lg _Ф – 3 – 1|  3 ,

отсюда . (3.6)

Частота _С желаемой ЛАЧХ принимается равной наименьшему из значений, рассчитанных по (3.5) и (3.6). Например, для рис. 3: по (3.5)

lg _С 1,7–0,75=0,95; по (3.6) lg _С (1,54+1,7–1)/2=1,145.

Выбираем lg _С=0,95 (_С=10^0,95=8,91 с^–1).

По приведенной выше методике может быть определена частота _С и построена желаемая ЛАЧХ L_Р^ЖЕЛ() и иной конфигурации.

Динамическая составляющая ЛАЧХ L_К^!() корректирующего устройства (коэффициент k_I учтен в k_{Р МАКС}) получается путем вычитания зависимости L_Р^НК() из L_Р^ЖЕЛ(), т. е.

L_К¹()= L_Р^ЖЕЛ()-L_Р^НК().

Полная ЛАЧХ корректирующего устройства

L_К()=lg k₁ + L_К¹().

В качестве схемотехнической реализации корректирующего устройства может быть рекомендован операционный усилитель, включенный по схеме рис. 4 а. Используя методику, изложенную в первой части задания, нетрудно получить передаточной функции в виде

. (3.7)

Рис. 4. К расчету корректирующего устройства: а – принципиальная схема; б…д – ЛАЧХ при различных параметрах

При различных вариациях параметров можно реализовать различные виды коррекции:

• опережающую (рис. 4 б) – при С3=0;

• запаздывающую (рис. 4 в) – при С2=0;

• комбинированные: (рис. 4 г) – при T₃>T₄>T₁>T_2;

(рис. 4 д) – при T₁>T₂>T₃>T₄.

Постоянные времени числителя передаточной функции (3.7) соответствуют частотам сопряжения аппроксимированной ЛАЧХ L_К() с положительным переходом, т. е. наклона с –1 на 0 или с 0 на +1, а знаменатель соответствует частотам сопряжения участков L_К() с отрицательным переходом, т. е. с 0 на –1 или с +1 на 0, если следовать по L_К() в сторону возрастания частот.

Рассматриваемому примеру соответствует коррекция вида, указанного на рис. 4 д. Частота сопряжения ₁=1/Т₁; ₂=1/Т₂; ₃=1/Т₃ и ₄=1/Т₄ легко получаются, если взять антилогарифм (десятичный) абсцисс, приведенных на рис. 3. По (3.7) можно составить систему пяти уравнений (четыре постоянные и k₁=R6/R4 c шестью неизвестными параметрами). Поэтому один из параметров необходимо определить. Рекомендуется задать значение С2=1 мкФ, а остальные параметры получить из решения системы уравнений

(3.8)

.

Рассчитать кривую переходного процесса n(t), отклонение n_З частоты вращения вала привода от заданного значения n_ЗАД при приложении заданного возмущения наиболее удобно с использованием программ MatLab и System View.

Показатели качества переходного процесса t_Р=t_ПП – время регулирования или время переходного процесса; – перерегулирование; М – колебательность.

1. Временем регулирования t_Р называется наименьший промежуток времени, по истечению которого кривая переходного процесса регулируемой величины будет (при своём дальнейшем изменении) отклонятся от установившегося значения не более чем на Δ. Примем Δ=5 % от Δn_∞.

2. Перерегулированием называется отношение разности между максимальным и установившимся значением регулируемой величины к её установившемуся значению, умноженному на 100 %:

3. Колебательность М переходного процесса характеризуется числом колебаний за время переходного процесса.