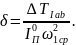- •Глава 1. Исходные данные для проектирования проектирование и исследование динамической нагруженности двс большегрузного автомобиля
- •Приложение
- •Глава 2. Блок-схема исследования динамики машинного агрегата
- •Глава 3. Динамический синтез и анализ машинного агрегата. Пункт 3.1. Задачи динамического синтеза и анализа.
- •Пункт 3.2. Структурный анализ исполнительного рычажного механизма.
- •Пункт 3.3 Определение основных размеров, масс и моментов инерции звеньев.
- •Пункт 3.4 Построение 12 планов положения механизма.
- •Пункт 3.5 Кинематический анализ механизма.
- •Подпункт 3.5.1 Графический метод кинематического анализа.
- •Подпункт 3.5.2 Аналитический метод расчета.
- •Пункт 3.6 Определение сил движущих действующих на поршень.
- •Пункт 3.7 Динамическая модель машинного агрегата.
- •Пункт 3.8 Определение приведенных моментов сил движущих и сил сопротивления.
- •Пункт 3.9 Определение переменной составляющей приведенного момента инерции
- •Пункт 3.10 Определение постоянной составляющей приведенного момента инерции и момента инерции маховика
- •Пункт 3.11 Определение закона вращения звена приведения
- •Пункт 3.12 Схема алгоритма программы исследования динамической нагруженности машинного агрегата
- •Пункт 3.13. Обработка результатов расчётов
- •Кинематические характеристики .
- •Переменная составляющая приведенного момента инерции и её слагаемые а, в, с.
- •Приведенный момент движущих сил и приведенный момент сил сопротивления .
- •Работа движущих сил и работа сил сопротивления .
- •Изменение кинетической энергии машины ∆t( и изменение кинетической энергии постоянной составляющей приведенного момента инерции ∆ .
- •Изменение угловой скорости ∆ и угловое ускорение звена приведения.
- •Пункт 3.14. Выводы
- •Глава 4. Динамический анализ рычажного механизма Пункт 4.1. Задачи динамического анализа
- •Пункт 4.2. Кинематический анализ механизма
- •Подпункт 4.2.1. Графический метод расчётов
- •Подпункт 4.2.2. Аналитический метод расчётов
- •Подпункт 4.2.3. Сопоставление расчётов
- •Пункт 4.3. Силовой расчёт
- •Подпункт 4.3.1. Графический метод расчётов
- •Подпункт 4.3.2. Аналитический метод
- •Пункт 4.4. Обработка результатов расчётов
- •Реакции и , действующие на звено 2.
- •Реакци в направляющих ползуна.
- •Годограф реакции .
- •Пункт 4.5. Выводы
- •Глава 5. Синтез кулачковых механизмов Пункт 5.1. Задачи синтеза
- •Пункт 5.2. Исходные данные для проектирования
- •Пункт 5.3. Определение кинематических характеристик
- •Пункт 5.4. Определение основных размеров кулачкового механизма
- •Пункт 5.5. Определение координат центрового профиля кулачка
- •11,69 Град.
- •Пункт 5.6. Построение графиков кинематических характеристик
- •Пункт 5.7. Построение графика угла давления
- •Пункт 5.8. Построение полной и упрощённой совмещённых диаграмм
- •Пункт 5.9. Построение центрового профиля кулачка
- •Пункт 5.10. Определение радиуса ролика и построение действительного профиля кулачка
- •Пункт 5.11. Определение жёсткости замыкающей пружины
- •Пункт 5.12. Выводы
- •Литература
Пункт 3.8 Определение приведенных моментов сил движущих и сил сопротивления.
Приведенный момент сил представляется в виде алгебраической суммы
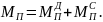
Определение выполняется из условия равенства мгновенных мощностей
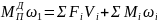
Откуда

где
 – проекции силы
– проекции силы
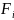 на оси координат;
на оси координат;
 -
проекции аналога скорости точки
приложения силы;
-
проекции аналога скорости точки
приложения силы;
 – передаточная
функция от i-го
звена, к которому приложен момент
– передаточная
функция от i-го
звена, к которому приложен момент
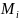 ,
к звену 1;
,
к звену 1;
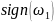 =
+1 при направлении вращения звена 1 против
часовой стрелки;
=
+1 при направлении вращения звена 1 против
часовой стрелки;
= - 1 при направлении вращения звена 1 по часовой стрелке.
В
формуле
силы
 ,
,
 и моменты
берутся со знаками, соответствующими
правой системе координат (положительное
направление вращения – против часовой
стрелки).
и моменты
берутся со знаками, соответствующими
правой системе координат (положительное
направление вращения – против часовой
стрелки).
Так,
для вертикального механизма (рис. 3.5)
определяется из равенства
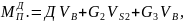
Y
X
A
B
3
2
1
O,
























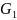
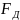




Рисунок 3.6.
Учитывая,
что
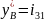 ,
,
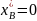 ,
,
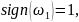 получим
получим
В
рассматриваемом положении сила
 имеет отрицательное значение, так как
она направленна в против положительного
направления оси X.
имеет отрицательное значение, так как
она направленна в против положительного
направления оси X.

Сила в изображенном случае положительна.
Приведенный момент движущих сил определяется из условия, что при установившемся режиме движения изменение кинетической энергии машины за цикл равно нулю, т.е.

откуда
за цикл
 .
.
Работа сил сопротивления вычисляется по формуле

Интегрирование выполняется численным методом по правилу трапеций:
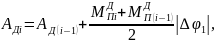
где
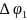 – шаг интегрирования в радианах.
– шаг интегрирования в радианах.
С
учетом
 при
при
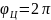
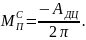
Пункт 3.9 Определение переменной составляющей приведенного момента инерции
Переменная составляющая определяется из условия равенства кинетических энергий, т.е. кинетическая энергия звена приведения, имеющего момент инерции , равна сумме кинетических энергий звеньев, характеризуемых переменными передаточными функциями:

Разделив
это выражение на
 ,
с учетом того что
,
с учетом того что
 ,
получим
,
получим

Для звеньев 2, 3 кривошипно-ползунного механизма (см рис. 3.5)
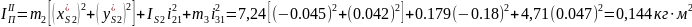
Производная
 , необходимая в последующем для определения
закона движения звена приведения, имеет
вид
, необходимая в последующем для определения
закона движения звена приведения, имеет
вид
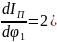
Пункт 3.10 Определение постоянной составляющей приведенного момента инерции и момента инерции маховика
В
основу расчета положен метод Н.И.
Мерцалова. Для определения изменения
кинетической энергии машины
 предварительно определяем работу
движущих сил
предварительно определяем работу
движущих сил
 .
Для i-го
положения
.
Для i-го
положения
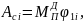
где

Тогда

Изменение
кинетической энергии
 звеньев с постоянным приведенным
моментом инерции
звеньев с постоянным приведенным
моментом инерции
 равно
равно

где
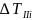 – кинетическая энергия звеньев, создающих
переменную составляющую
– кинетическая энергия звеньев, создающих
переменную составляющую
 .
По методу Н.И. Мерцалова
определяется приближённо по средней
угловой скорости
:
.
По методу Н.И. Мерцалова
определяется приближённо по средней
угловой скорости
:

Далее
из полученного цикла массива значений
(рис. 3.6) находим максимальную
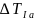 и минимальную
и минимальную
 величины, используя которые вычисляем
максимальный перепад кинетической
энергии энергии:
величины, используя которые вычисляем
максимальный перепад кинетической
энергии энергии:
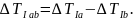
∆T
(для
)
О
∆
∆
∆
∆
∆
,
∆
∆T
∆
(для ∆
)
1
цикл
O
b
a
































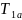
Рисунок 3.7
Тогда
необходимая величина
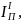 при которой имеет место вращения звена
приведения с заданным коэффициентом
неравномерности δ, равна
при которой имеет место вращения звена
приведения с заданным коэффициентом
неравномерности δ, равна
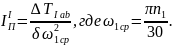
Момент инерции маховика определяется по формуле

где
 – приведенный момент инерции всех
вращающихся масс машины (ротора двигателя,
зубчатых колес, кривошипа).
– приведенный момент инерции всех
вращающихся масс машины (ротора двигателя,
зубчатых колес, кривошипа).
Иногда величины может оказаться больше полученного значения . В этом случае не требуется установки маховика. Тогда реальный коэффициент неравномерности вращения равен