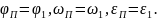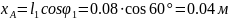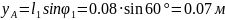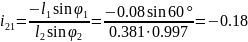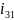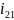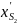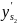- •Глава 1. Исходные данные для проектирования проектирование и исследование динамической нагруженности двс большегрузного автомобиля
- •Приложение
- •Глава 2. Блок-схема исследования динамики машинного агрегата
- •Глава 3. Динамический синтез и анализ машинного агрегата. Пункт 3.1. Задачи динамического синтеза и анализа.
- •Пункт 3.2. Структурный анализ исполнительного рычажного механизма.
- •Пункт 3.3 Определение основных размеров, масс и моментов инерции звеньев.
- •Пункт 3.4 Построение 12 планов положения механизма.
- •Пункт 3.5 Кинематический анализ механизма.
- •Подпункт 3.5.1 Графический метод кинематического анализа.
- •Подпункт 3.5.2 Аналитический метод расчета.
- •Пункт 3.6 Определение сил движущих действующих на поршень.
- •Пункт 3.7 Динамическая модель машинного агрегата.
- •Пункт 3.8 Определение приведенных моментов сил движущих и сил сопротивления.
- •Пункт 3.9 Определение переменной составляющей приведенного момента инерции
- •Пункт 3.10 Определение постоянной составляющей приведенного момента инерции и момента инерции маховика
- •Пункт 3.11 Определение закона вращения звена приведения
- •Пункт 3.12 Схема алгоритма программы исследования динамической нагруженности машинного агрегата
- •Пункт 3.13. Обработка результатов расчётов
- •Кинематические характеристики .
- •Переменная составляющая приведенного момента инерции и её слагаемые а, в, с.
- •Приведенный момент движущих сил и приведенный момент сил сопротивления .
- •Работа движущих сил и работа сил сопротивления .
- •Изменение кинетической энергии машины ∆t( и изменение кинетической энергии постоянной составляющей приведенного момента инерции ∆ .
- •Изменение угловой скорости ∆ и угловое ускорение звена приведения.
- •Пункт 3.14. Выводы
- •Глава 4. Динамический анализ рычажного механизма Пункт 4.1. Задачи динамического анализа
- •Пункт 4.2. Кинематический анализ механизма
- •Подпункт 4.2.1. Графический метод расчётов
- •Подпункт 4.2.2. Аналитический метод расчётов
- •Подпункт 4.2.3. Сопоставление расчётов
- •Пункт 4.3. Силовой расчёт
- •Подпункт 4.3.1. Графический метод расчётов
- •Подпункт 4.3.2. Аналитический метод
- •Пункт 4.4. Обработка результатов расчётов
- •Реакции и , действующие на звено 2.
- •Реакци в направляющих ползуна.
- •Годограф реакции .
- •Пункт 4.5. Выводы
- •Глава 5. Синтез кулачковых механизмов Пункт 5.1. Задачи синтеза
- •Пункт 5.2. Исходные данные для проектирования
- •Пункт 5.3. Определение кинематических характеристик
- •Пункт 5.4. Определение основных размеров кулачкового механизма
- •Пункт 5.5. Определение координат центрового профиля кулачка
- •11,69 Град.
- •Пункт 5.6. Построение графиков кинематических характеристик
- •Пункт 5.7. Построение графика угла давления
- •Пункт 5.8. Построение полной и упрощённой совмещённых диаграмм
- •Пункт 5.9. Построение центрового профиля кулачка
- •Пункт 5.10. Определение радиуса ролика и построение действительного профиля кулачка
- •Пункт 5.11. Определение жёсткости замыкающей пружины
- •Пункт 5.12. Выводы
- •Литература
Подпункт 3.5.2 Аналитический метод расчета.
Расчет выполняем методом замкнутого векторного контура. Расчетная схема представлена на рис 3.4.
B
Y










3


X
A
2
1
O





















Рисунок 3.4
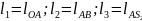 .
.
Основное
уравнение замкнутого векторного контура
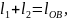 уравнение проецируется на координатной
оси, и уравнение проекции дифференцируется
по обобщенной координате
.
После первого дифференцирования получим
уравнение выражения для аналогов
скоростей, а при повторном дифференцировании
- получим уравнение для аналогов
ускорения.
уравнение проецируется на координатной
оси, и уравнение проекции дифференцируется
по обобщенной координате
.
После первого дифференцирования получим
уравнение выражения для аналогов
скоростей, а при повторном дифференцировании
- получим уравнение для аналогов
ускорения.
Для вертикальных механизмов расчет вычислений имеет вид:
8.
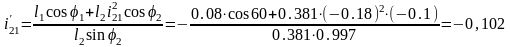
9.
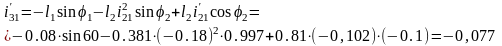
10.
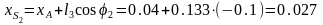
11.
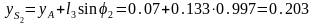
12.
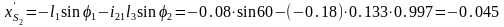
13.
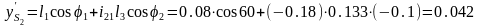
14.
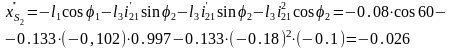
15.
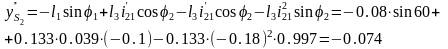
16.
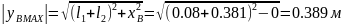
17
.
Таблица 3.1
Параметры |
Единицы измерения |
Аналитический метод |
Графический метод |
|
м |
0.047 |
0.045 |
|
- |
-0.18 |
0.184 |
|
м |
-0.045 |
0.044 |
|
м |
0.042 |
0.045 |
Пункт 3.6 Определение сил движущих действующих на поршень.
На
листе 1 изображаем индикаторную диаграмму
давлений в цилиндре. Для этого задаемся
максимальной ординатой давления
 .
Тогда:
.
Тогда:
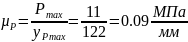
Значение ординат давлений в каждом положении записываем в таблицу 3.2:
Таблица 3.2
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
98 |
100 |
55 |
25 |
11 |
8 |
8 |
6 |
2 |
4 |
23 |
55 |
98 |
|
8,82 |
9 |
4,95 |
2,25 |
0,99 |
0,72 |
0,72 |
0,54 |
0,18 |
0,36 |
2,07 |
4,95 |
8,82 |
|
61177 |
62426 |
34334 |
15606 |
6866 |
4994 |
4994 |
3745 |
1248 |
2497 |
14358 |
34334 |
61177 |
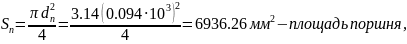
где
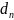 - диаметр поршня;
- диаметр поршня;
Формула, по которой рассчитываем давление в поршне:
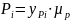

Определяем силу, действующую в поршнях:


Пункт 3.7 Динамическая модель машинного агрегата.
В движении входного звена исполнительного рычажного механизма имеют место колебания угловой скорости, основными причинами которых являются:
несовпадение законов изменения сил сопротивления и движущих сил в каждый момент времени;
непостоянство приведенного момента инерции звеньев исполнительного и некоторых вспомогательных магазинов.
Чтобы учесть влияние названных причин на закон движения входного звена исполнительного механизма, составляться упрощенная модель машинного агрегата и на основе – математическая модель, устанавливающая функциональную взаимосвязь исследуемых параметров.
Наиболее простой динамической моделью машинного агрегата может быть одномассавая модель, представленная на рис. 3.5.







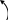























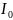




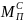
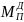




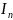
Рисунок 3.5
В
качестве такой модели рассматривается
условное вращающееся звено – звено
приведения, которое имеет момент инерции
 относительно оси вращения (приведенный
момент инерции) и находиться под действием
сил
относительно оси вращения (приведенный
момент инерции) и находиться под действием
сил
 (приведенного момента сил). В свою очередь
(приведенного момента сил). В свою очередь
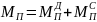 ,
где
,
где
 – приведенный момент движущих сил;
– приведенный момент движущих сил;
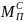 – приведенный момент сил сопротивления.
Кроме того,
– приведенный момент сил сопротивления.
Кроме того,
 где
– постоянная составляющая приведенного
момента инерции;
где
– постоянная составляющая приведенного
момента инерции;
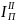 – переменная составляющая приведенного
момента инерции. В величину
– переменная составляющая приведенного
момента инерции. В величину
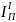 входят собственный момент инерции
кривошипа (
входят собственный момент инерции
кривошипа ( ,
приведенные моменты инерции ротора
электродвигателя и передаточного
механизма (
,
приведенные моменты инерции ротора
электродвигателя и передаточного
механизма (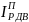 ,
,
 а также момента инерции
добавочной массы (маховика), причем
необходимость установки маховика
определяется на основании заданной
степени неравномерности движения звена
приведения.
а также момента инерции
добавочной массы (маховика), причем
необходимость установки маховика
определяется на основании заданной
степени неравномерности движения звена
приведения.
Динамические
характеристики
и
 должны быть такими, чтобы закон вращения
звена приведения был таким же, как и у
главного вала машины (кривошипа 1
основного исполнительного рычажного
механизма), т.е.
должны быть такими, чтобы закон вращения
звена приведения был таким же, как и у
главного вала машины (кривошипа 1
основного исполнительного рычажного
механизма), т.е.