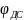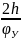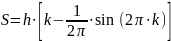- •Глава 1. Исходные данные для проектирования проектирование и исследование динамической нагруженности двс большегрузного автомобиля
- •Приложение
- •Глава 2. Блок-схема исследования динамики машинного агрегата
- •Глава 3. Динамический синтез и анализ машинного агрегата. Пункт 3.1. Задачи динамического синтеза и анализа.
- •Пункт 3.2. Структурный анализ исполнительного рычажного механизма.
- •Пункт 3.3 Определение основных размеров, масс и моментов инерции звеньев.
- •Пункт 3.4 Построение 12 планов положения механизма.
- •Пункт 3.5 Кинематический анализ механизма.
- •Подпункт 3.5.1 Графический метод кинематического анализа.
- •Подпункт 3.5.2 Аналитический метод расчета.
- •Пункт 3.6 Определение сил движущих действующих на поршень.
- •Пункт 3.7 Динамическая модель машинного агрегата.
- •Пункт 3.8 Определение приведенных моментов сил движущих и сил сопротивления.
- •Пункт 3.9 Определение переменной составляющей приведенного момента инерции
- •Пункт 3.10 Определение постоянной составляющей приведенного момента инерции и момента инерции маховика
- •Пункт 3.11 Определение закона вращения звена приведения
- •Пункт 3.12 Схема алгоритма программы исследования динамической нагруженности машинного агрегата
- •Пункт 3.13. Обработка результатов расчётов
- •Кинематические характеристики .
- •Переменная составляющая приведенного момента инерции и её слагаемые а, в, с.
- •Приведенный момент движущих сил и приведенный момент сил сопротивления .
- •Работа движущих сил и работа сил сопротивления .
- •Изменение кинетической энергии машины ∆t( и изменение кинетической энергии постоянной составляющей приведенного момента инерции ∆ .
- •Изменение угловой скорости ∆ и угловое ускорение звена приведения.
- •Пункт 3.14. Выводы
- •Глава 4. Динамический анализ рычажного механизма Пункт 4.1. Задачи динамического анализа
- •Пункт 4.2. Кинематический анализ механизма
- •Подпункт 4.2.1. Графический метод расчётов
- •Подпункт 4.2.2. Аналитический метод расчётов
- •Подпункт 4.2.3. Сопоставление расчётов
- •Пункт 4.3. Силовой расчёт
- •Подпункт 4.3.1. Графический метод расчётов
- •Подпункт 4.3.2. Аналитический метод
- •Пункт 4.4. Обработка результатов расчётов
- •Реакции и , действующие на звено 2.
- •Реакци в направляющих ползуна.
- •Годограф реакции .
- •Пункт 4.5. Выводы
- •Глава 5. Синтез кулачковых механизмов Пункт 5.1. Задачи синтеза
- •Пункт 5.2. Исходные данные для проектирования
- •Пункт 5.3. Определение кинематических характеристик
- •Пункт 5.4. Определение основных размеров кулачкового механизма
- •Пункт 5.5. Определение координат центрового профиля кулачка
- •11,69 Град.
- •Пункт 5.6. Построение графиков кинематических характеристик
- •Пункт 5.7. Построение графика угла давления
- •Пункт 5.8. Построение полной и упрощённой совмещённых диаграмм
- •Пункт 5.9. Построение центрового профиля кулачка
- •Пункт 5.10. Определение радиуса ролика и построение действительного профиля кулачка
- •Пункт 5.11. Определение жёсткости замыкающей пружины
- •Пункт 5.12. Выводы
- •Литература
Пункт 5.2. Исходные данные для проектирования
Схема кулачкового механизма представлена на рисунке 5.1.

Рис. 5.1.
Исходные данные представлены в таблице 5.1.
Таблица 5.1
Ход толкателя, h, м |
Фазовые углы, град |
Допускаемый
угол давления
|
е, м |
Законы движения толкателя |
||||||
|
|
|
при удалении |
При возвращении |
||||||
0,025 |
70 |
15 |
70 |
32 |
Не задан |
Синусоидальный |
Синусоидальный |
|||
Угловая
скорость вращения кулачка
 .
.
Масса
толкателя
 .
.
Пункт 5.3. Определение кинематических характеристик
Переведём значения фазовых углов в радианную меру:
 ;
;
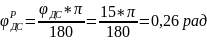 ;
;
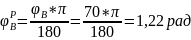 .
.
Рабочий угол кулачка:
 .
.
Так как при вычислении с помощью ЭВМ фазовые углы удаления и возвращения разделены на 12 участков каждый, вычислим приращения угла поворота кулачка (шаг) на обеих фазах:
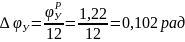 ;
;
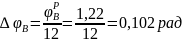 .
.
Кинематические характеристики вычисляются с учётом номера положения i (на фазе удаления номера меняются от 1 до 13, при возвращении — от 14 до 26), входящего в позиционный коэффициент k.
В контрольном положении 3 позиционный коэффициент равен:
 .
.
Поскольку на фазе удаления толкатель движется по синусоидальному закону кинематические характеристики определяются в следующем порядке.
Таблица 5.2
Формулы |
Экстремальные значения |
Закон постоянного ускорения
|
|
|
|
|
h |
Кинематические характеристики получены для фазового угла:
 рад.
рад.
На
фазе возвращения кинематические
характеристики вычисляются в соответствии
с тем же законом, но необходимо внести
следующие изменения: угол
заменить на
,
формулы для
 использовать со знаком «минус», а отсчёт
коэффициента k
брать с конца фазы, т.е. принимать
использовать со знаком «минус», а отсчёт
коэффициента k
брать с конца фазы, т.е. принимать
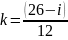 ,
причём 14
,
причём 14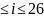 .
.
Тогда, приняв за контрольное положение 22, получим:
 ;
;
 м.
м.
Аналог скорости движения толкателя:
 м.
м.
Аналог ускорения:
 м.
м.
Кинематические характеристики получены для фазового угла:
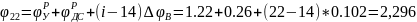 рад.
рад.
Пункт 5.4. Определение основных размеров кулачкового механизма
Основные размеры механизма определяются из условия ограничения угла давления. При этом приближённо можно принять, что угол давления имеет наибольшую величину в тех положениях механизма, в которых аналог скорости толкателя достигает экстремальных значений на фазах удаления и возвращения. В ряде случаев это может приводить к некоторому превышению максимально допустимой величины угла давления в отдельных положениях.
В качестве расчётной схемы принимаем схему механизма изображённую на рисунке 5.2, в которой кулачок вращается против часовой стрелки.
y
x
e
О




















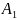
Рис. 5.2.
Для
определения минимального радиуса
кулачка строим упрощённую совмещённую
диаграмму
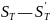 (Рис. 5.3). По оси
(Рис. 5.3). По оси
 от точки
откладываем отрезок
от точки
откладываем отрезок
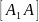 ,
соответствующий перемещению толкателя
,
соответствующий перемещению толкателя
 ,
при котором аналог скорости на фазе
удаления имеет наибольшее значение
,
при котором аналог скорости на фазе
удаления имеет наибольшее значение
 .
От точки А влево откладываем отрезок
.
От точки А влево откладываем отрезок
 ,
соответствующий
.
Для фазы возвращения, аналогично,
откладываем отрезок
,
соответствующий
.
Для фазы возвращения, аналогично,
откладываем отрезок
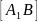 ,
соответствующий перемещению толкателя
,
при котором аналог скорости на фазе
возвращения максимален
,
соответствующий перемещению толкателя
,
при котором аналог скорости на фазе
возвращения максимален
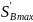 .
От точки a
и b
под углами
проводим лучи до пересечения и образования
заштрихованной зоны. Вершина заштрихованной
зоны является центром вращения кулачка
при минимальных размерах механизма для
заданного угла давления.
.
От точки a
и b
под углами
проводим лучи до пересечения и образования
заштрихованной зоны. Вершина заштрихованной
зоны является центром вращения кулачка
при минимальных размерах механизма для
заданного угла давления.
M
O
e
B
b
A
a





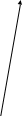




























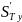
Рис. 5.3.
Максимальное значение аналога скорости на фазе удаления:
 м.
м.
Максимальное значение аналога скорости на фазе возвращения:
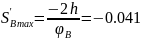 м.
м.
Перемещения толкателя в тех положениях, где аналог скорости максимален на фазе удаления и возвращения:
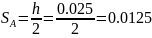 м;
м;
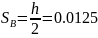 м.
м.
Тогда:
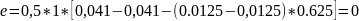 м;
м;
 м;
м;
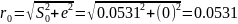 м.
м.

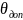 ,
град
,
град