Подпункт 4.3.2. Аналитический метод

Расчётные схемы группы Ассура 2-го вида показаны на рисунке 4.1.

Y

3

B

2

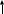
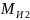
1

A

X

O

Рис. 4.1.

К звеньям (2,3) группы приложим внешнюю нагрузку , силы тяжести звеньв , . Реакцию во вращательной кинематической паре А представим в виде проекций 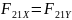. Реакция в поступательной кинематической паре В перпендикулярна направлению перемещения ползуна и в данном случае проходит через точку В.

В соответствии с принципом Даламбера приложим к звеньям (2,3) инерционные нагрузки.

Проекции главного вектора сил инерции звена 2:

;

,

главный момент сил инерции звена 2:

,

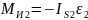главный вектор сил инерции звена 3:

.

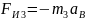Силы тяжести звеньев равны:

;

.

Реакции в кинематических парах группы (2,3) с вертикальным расположением ползуна вычисляются в следующей очерёдности:

1. Из условия, что , определяются :

.

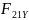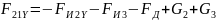2. Реакция 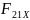определяется из уравнения равновесия моментов сил для звена 2 относительно точки В:

.

3. Реакция определяется из условия равновесия проекций сил, действующих на группу (2,3), на ось X:

.

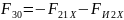Для определения проекций и 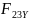реакции во внутренней кинематической паре. Рассмотрим равновесие звена 2 под действием приложенных сил:

,

откуда, проектируя на оси координат, получим:

;

.

Модули реакций и 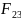определяем по формулам:

;

.

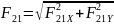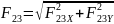Направление реакций и установим, определив углы наклона их к оси X:

;

;

;

.

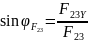Далее рассматривается кривошип 1 (рисунок 4.2).

y

А

1

O,

x

Рис. 4.2.

В точке А приложена известная реакция , проекции которой равны:

;

.

В точке О расположена сила тяжести 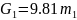и неизвестная реакция . Кроме того, к звену приложен известный главный момент сил инерции:

.

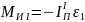Для того, чтобы звено 1 двигалось по заданному закону, к нему приложен уравновешивающий момент сил , который является реактивным моментом со стороны отсоединённой части машины. Его величина определяется из уравнения моментов сил относительно точки О:

.

Реакция в проекциях имеет вид:

;

.

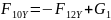Модуль:

.

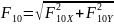Направление определяется углом 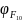по формулам:

;

.

На основании вышеизложенного можно представить алгоритм силового расчёта кривошипно-шатунного механизма:

1. ;

2. Н;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. Н;

14. Н;

15. Н;

16. ;

17. Н;

18. Н;

19. Н;

20. Н;

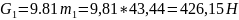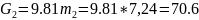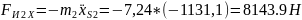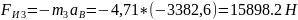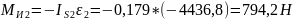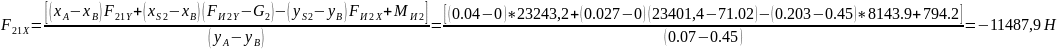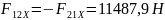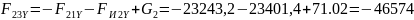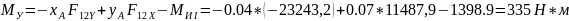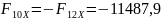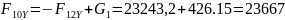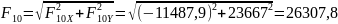21. Н.

Сопоставление результатов расчётов для положения 2 приведено в таблице 4.2.

Таблица 4.2

Параметр	Ед. изм	Графический метод	Аналитический метод
	Н	27800	26307,8
	Н	27400	25927,2
	Н	46800	46693,9
	Н	3200	3344
		339,2	335